数字三角形
时间限制:2 sec
空间限制:256 MB
问题描述
给定一个高度为 n 的“数字三角形”,其中第 i 行(1<=i<=n)有 i 个数。(例子如下图所示)
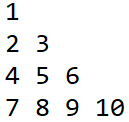
初始时,你站在“数字三角形”的顶部,即第一行的唯一一个数上。每次移动,你可以选择移动到当前位置正下方或者当前位置右下方的位置上。即如果你在 (i,j)(表示你在第i行从左往右数第j个数上,下同),你可以选择移动到 (i+1,j) 或 (i+1,j+1)。
你想让你经过的所有位置(包括起点和终点)的数字总和最大。求这个最大值。
输入格式
第一行一个正整数 n,表示数字三角形的大小。
第 2 行到第 n+1 行,第 i+1 行为 i 个用空格隔开的非负整数,描述数字三角形的第 i 行。
输出格式
一行一个整数,表示经过路径上数的最大总和。
样例输入
4
1
2 3
4 5 6
7 8 9 10
样例输出
20
样例解释
不停地向右下走即可。
数据范围
对于 50% 的数据,保证 n<=5。
对于 100% 的数据,保证 n<=1,000,保证数字三角形内的数不超过 10^6。
提示
[如果我们使用搜索算法,我们会在搜索时记录哪些信息呢?]
[当前到达的点的坐标、当前经过路径上数的总和!]
[总和显然是越大越好!]
[于是可以设计出状态:dp[i][j] 表示走到坐标为 (i,j) 的点时的最大总和。]
[很容易就可以设计出状态转移方程啦!]
代码实现
def max_path_sum(triangle):
n = len(triangle)
dp = [[0] * n for _ in range(n)]
# 初始化第一行
dp[0][0] = triangle[0][0]
# 动态规划,计算最大总和
for i in range(1, n):
for j in range(i + 1):
if j == 0:
dp[i][j] = triangle[i][j] + dp[i-1][j]
elif j == i:
dp[i][j] = triangle[i][j] + dp[i-1][j-1]
else:
dp[i][j] = triangle[i][j] + max(dp[i-1][j], dp[i-1][j-1])
# 返回最后一行的最大总和
return max(dp[-1])
# 读取输入
n = int(input())
triangle = []
for _ in range(n):
row = list(map(int, input().split()))
triangle.append(row)
# 输出结果
result = max_path_sum(triangle)
print(result)
背包问题1
描述
n种物品,每种物品有相应的价值和体积,同时物品还分为两类,一类是“单个物品”,即该种物品只有一个;一类是“多个物品”,即该种物品有无限个。
现在你有一个体积为V的背包,那么该装些什么物品到背包里使得价值之和最大呢?
输入
第一行包含两个正整数n,V。
接下来n行,每行代表一种物品。每行的第一个数字表示该物品的种类(若为0表示“单个物品”,若为1表示“多个物品”),第二个数字表示该物品的价值,第三个数字表示该物品的体积。
输出
输出一个整数,表示最大的价值之和。
样例1输入
5 8
0 6 8
0 7 3
1 1 1
0 8 1
0 5 2
样例1输出
22
样例1解释
第三种物品有无限个,其余都是单个物品。
若我们放入物品1,则背包已经装满,此时价值和为6;
若我们放入物品2、4、5,背包所剩体积为8-3-1-2=2,此时价值和为7+8+5=20;
若我们放入8个物品3,背包装满,此时价值之和为8×1=8;
若我们放入物品2、4、5,再放两个物品3,则背包装满,此时价值和为7+8+5+2×1=22。
可以验证,最优答案就是22。
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
对于30%的数据,n,V ≤ 20;
对于100%的数据,n,V ≤ 5000。
保证数据中所有的整数均为正整数,且不超过5000。
时间:6 sec
空间:512 MB
提示
[经典的01背包和完全背包问题。]
代码实现
def knapsack(n, V, items):
dp = [0] * (V + 1)
for i in range(n):
if items[i][0] == 0: # 单个物品
for j in range(V, items[i][2] - 1, -1):
dp[j] = max(dp[j], dp[j - items[i][2]] + items[i][1])
else: # 多个物品,转化为完全背包问题
for j in range(items[i][2], V + 1):
dp[j] = max(dp[j], dp[j - items[i][2]] + items[i][1])
return dp[V]
if __name__ == "__main__":
n, V = map(int, input().split())
items = []
for _ in range(n):
item = list(map(int, input().split()))
items.append(item)
result = knapsack(n, V, items)
print(result)
背包问题2
描述
n个物品,每个物品有一个体积v和价值w。现在你要回答,把一个物品丢弃后,剩下的物品装进一个大小为V的背包里能得到的最大价值是多少。
输入
输入的第一行包含一个正整数n(n ≤ 5000)。
接下来n行,每行包含两个正整数v和w(v,w ≤ 5000),分别表示一个物品的体积和价值。
接下来一行包含一个正整数q(q ≤ 5000),表示询问个数。
接下来q行,每行包含两个正整数V和x(V ≤ 5000,x ≤ n),表示询问将物品x丢弃以后剩下的物品装进一个大小为V的背包能得到的最大价值。
输出
输出q行,每行包含一个整数,表示询问的答案。
样例1输入
3
3 5
2 2
1 2
3
3 1
3 2
3 3
样例1输出
4
5
5
样例1解释
有3个物品,第一个物品的体积为3、价值为5,第二个物品体积为2、价值为2,第三个物品体积为1、价值为2。
有3个询问:
第一个询问是问去掉1物品后剩下的2、3物品填进一个大小为3的背包能得到的最大价值。显然2、3物品都是可以放进背包的,所以最大价值为2+2=4。
第二个询问是问去掉2物品后剩下的1、3物品填进一个大小为3的背包能得到的最大价值。若我们填3物品,我们只能得到价值2;若我们填1物品,则可以得到价值5。所以最大价值为5。
第三个询问我们同样也是填1物品,最大价值为5。
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
对于30%的数据,n,q,v,V,w ≤ 10;
对于50%的数据,n,q,v,V,w ≤ 200。
时间:10 sec
空间:512 MB
提示
[我们可以预处理“前缀背包”、“后缀背包”,然后询问时做“背包合并”的操作。]
代码实现
def get_answer(n, vw, q, queries):
v = [-1] + [vw[i][0] for i in range(n)]
w = [-1] + [vw[i][1] for i in range(n)]
d = [[0] * 5005 for _ in range(5005)]
for i in range(1, n + 1):
for V in range(v[i]):
d[i][V] = d[i - 1][V]
for V in range(v[i], 5001):
d[i][V] = max(d[i - 1][V], d[i - 1][V - v[i]] + w[i])
f = [[0] * 5005 for _ in range(5005)]
for i in range(n, 0, -1):
for V in range(v[i]):
f[i][V] = f[i + 1][V]
for V in range(v[i], 5001):
f[i][V] = max(f[i + 1][V], f[i + 1][V - v[i]] + w[i])
ans = []
for query in queries:
V, x = query
mx = 0
for i in range(V + 1):
mx = max(mx, d[x - 1][i] + f[x + 1][V - i])
ans.append(mx)
return ans
if __name__ == "__main__":
n = int(input())
vw = [list(map(int, input().split())) for _ in range(n)]
q = int(input())
queries = [list(map(int, input().split())) for _ in range(q)]
ans = get_answer(n, vw, q, queries)
for i in ans:
print(i)