今日题目:
- 226. 翻转二叉树
- 101. 对称二叉树
- 114. 二叉树展开为链表
目录
- LC 226. 翻转二叉树 【easy】
- LC 101. 对称二叉树 ⭐⭐⭐
- LC 114. 二叉树展开为链表 ⭐⭐⭐
今天的题目主要是对二叉树递归遍历的应用,东哥带你刷二叉树(思路篇) | labuladong 文章对二叉树解题的思维模式进行了总结:
二叉树解题的思维模式分两类:
- 【“遍历”思维】是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
- 【“分解问题”思维】是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
今天的题目就展示了“遍历”的思维和“分解问题”的思维的区别和联系。做其中两个题时有点不顺利,所以这部分思维的训练需要着重加强。
LC 226. 翻转二叉树 【easy】
226. 翻转二叉树 | LeetCode
这个题目可以通过递归遍历轻松解决,难度不大。
LC 101. 对称二叉树 ⭐⭐⭐
101. 对称二叉树 | LeetCode
一开始做这个题,是想着用层序遍历的模板来解,但其实并不可以,层序遍历无法得知树的结构,因此无法判别结构上是否对称。
这个题目需要巧妙地使用好二叉树的递归。递归不是必须对一个节点的 left 和 right 进行递归,在这个题目中我们拓展了思路,可以根据具体题目需要,对不同节点继续递归:
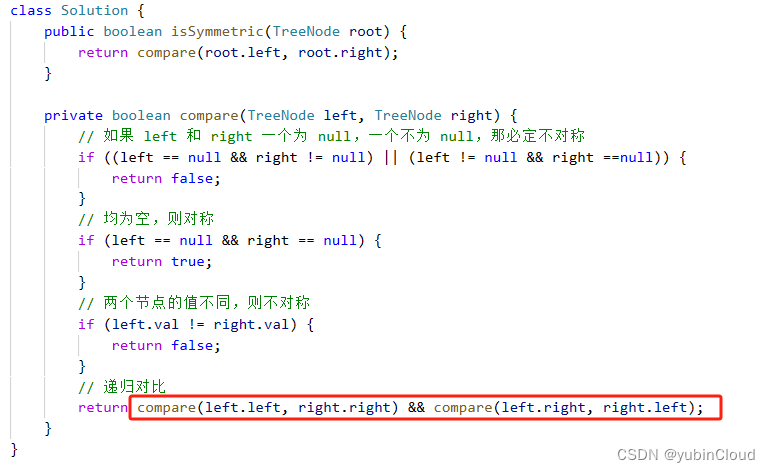
在这个题目中,代码对对称的两个子节点进行 compare。
LC 114. 二叉树展开为链表 ⭐⭐⭐
114. 二叉树展开为链表
这个题目一开始也没想到思路,主要在于没有抓住对“子问题”的解决,也就是在一个局部节点上该怎么做。
通过这个题目,我们学会了用“分解问题”的思维去解决问题。比如在这个题目中,通过解决了将一个局部节点先 flatten,再基于此将更大范围的节点进行 flatten。
这个问题的详细解决思路,可以参考 东哥带你刷二叉树(思路篇) - 将二叉树展开为链表 | labuladong。








![LeetCode 刷题 [C++] 第98题.验证二叉搜索树](https://img-blog.csdnimg.cn/direct/0969958fe1194ce59312733623e4c43f.png)