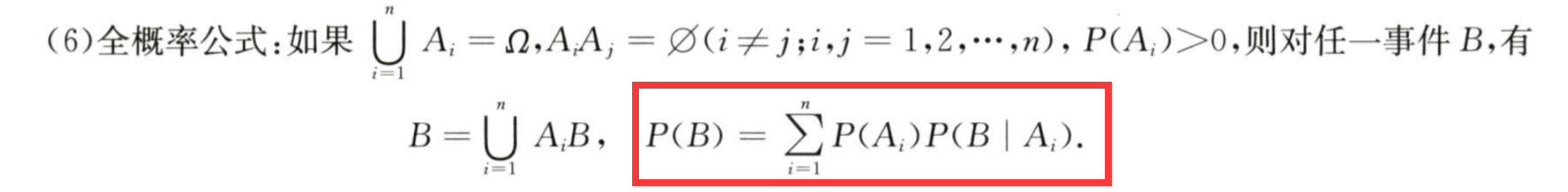第一课 随机事件和概率
1/6 无放回类题目(一次摸多个)
例 1. 盒子里有 3 绿 4 红共 7 个小球,无放回的摸 3 个试求摸出 1 绿 2 红的概率 例 2. 钱包里有 3 张 100 元, 5 张 10 元, 3 张 5 元的纸币,随机摸 3 张,试求摸出 1 张 100 , 2 张 10 的概率 例1.盒子里有3绿4红共7个小球,无放回的摸3个试求摸出1绿2红的概率\\ 例2.钱包里有3张100元,5张10元, 3张5元的纸币,随机摸3张,试求摸出1张100,2张10的概率 例1.盒子里有3绿4红共7个小球,无放回的摸3个试求摸出1绿2红的概率例2.钱包里有3张100元,5张10元,3张5元的纸币,随机摸3张,试求摸出1张100,2张10的概率
【无放回,直接用C解】
古典概型

排列与组合
2/6 有放回题目(进行多次,每次情况一致)

3/6 事件的概率

4/6 条件概率
①条件概率
②相互独立

法二:
P
(
A
‾
∣
B
)
=
1
−
P
(
A
∣
B
)
=
1
−
P
(
A
B
)
P
(
B
)
由于
A
B
相互独立,所以
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P
(
A
‾
∣
B
)
=
1
−
P
(
A
∣
B
)
=
1
−
P
(
A
)
P
(
B
)
P
(
B
)
=
0.6
P(\overline A|B)= 1-P(A|B)=1-\frac{P(AB)}{P(B)}\\ 由于AB相互独立,所以P(AB)=P(A)P(B)\\ P(\overline A|B)= 1-P(A|B)=1-\frac{P(A)P(B)}{P(B)}=0.6\\
P(A∣B)=1−P(A∣B)=1−P(B)P(AB)由于AB相互独立,所以P(AB)=P(A)P(B)P(A∣B)=1−P(A∣B)=1−P(B)P(A)P(B)=0.6
5/6 全概率公式

6/6 贝叶斯公式
贝叶斯其实是条件概率反过来求。其实就是**已知结果求原因**