python GPU加速以numba为例

GPU编程(CUDA)

GPU(图形处理单元)，多核系统，而现今的大多数CPU也属于多核系统，但它们之间还是存在很大的区别:

CPU适合执行复杂的逻辑，比如多分支，其核心比较重(复杂)
GPU适合执行简单的逻辑，大量的数据计算，其吞吐量更高，但是核心比较轻(结构简单)
GPU本职任务时做图形图像的，将数据处理成图像，再显示。其最初是不可编程的，但后面有hacker为了实现规模较大的运算，开始研究着色语言或图形处理原语来和GPU对话，英伟达发现是商机就开发了一套平台 CUDA 专门用于GPU编程，然后深度学习火了，CUDA就越来越火，再到现在的AIGC的普及化，利用CUDA优化大规模计算基本是共识了。
异构运算
处理器不是单一类型组成的，比如仅有CPU，都是异构架构，反之就是同构架构。
异构架构比同构架构运算量更大，但是其应用复杂度也更高，控制、传输都需要人为干预，而同构架构，硬件部分自己完成控制，不需要人为设计。
在CPU+GPU的异构架构里
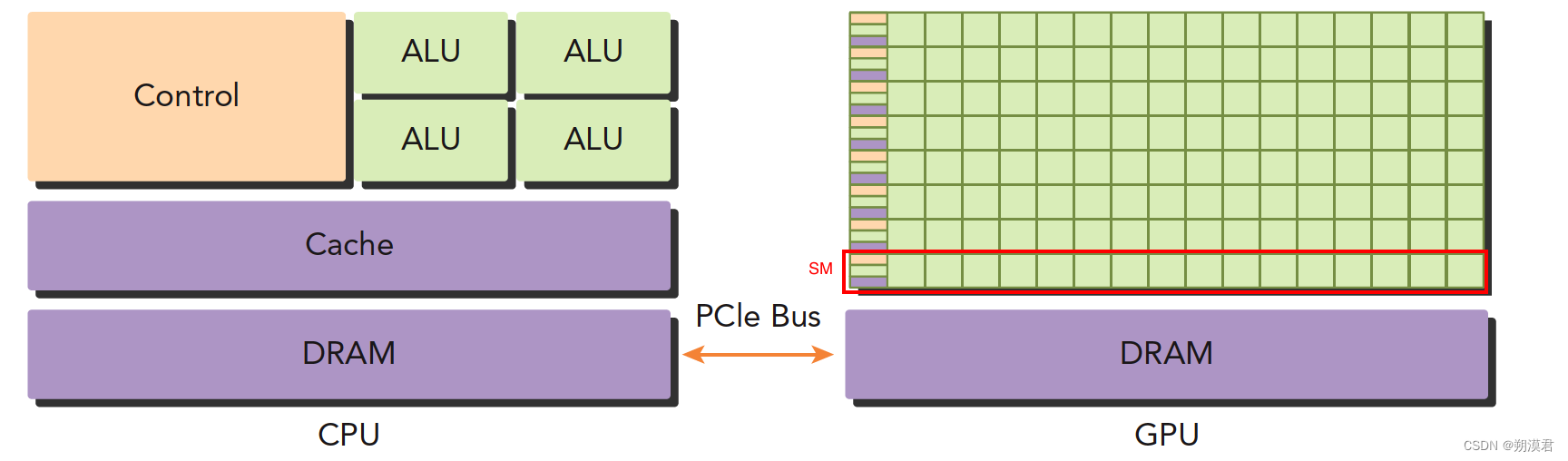
左图一个4核CPU 一般有4个ALU，DRAM是内存，CPU通过总线访问内存，Cache 高速缓冲存储器
右图 GPU 一个绿色小方块就是一个ALU，而红框标记的SM表示这一组的ALU公用一个Control单元和Cache，就相当于一个多核CPU，但ALU更多，且control变小，导致计算力提升，控制能力减弱，所以对于控制逻辑复杂的程序，一个GPU的SM是没办法和CPU比较的，但对于逻辑简单，数据量大的任务，GPU更加高效。
CPU和GPU之间通过PCle总线连接，用于传递指令和数据(这也是决定性能瓶颈的地方之一)

一个在异构平台上的运行的程序，应该将低并行复杂逻辑的部分在CPU上跑，将高并行简单逻辑的部分在GPU上跑
CPU和GPU的区别：

CPU线程是重量级实体，操作系统交替执行线程，线程上下文切换花销很大
GPU线程是轻量级的，GPU的应用一般包含成千上万的线程，多数都在排队状态，线程之间切换基本没有开销
CPU的核被设计用来尽可能减少一个或两个线程运行时间的延迟，而GPU核则是大量线程，最大幅度提高吞吐量
cuda：一种异构计算平台

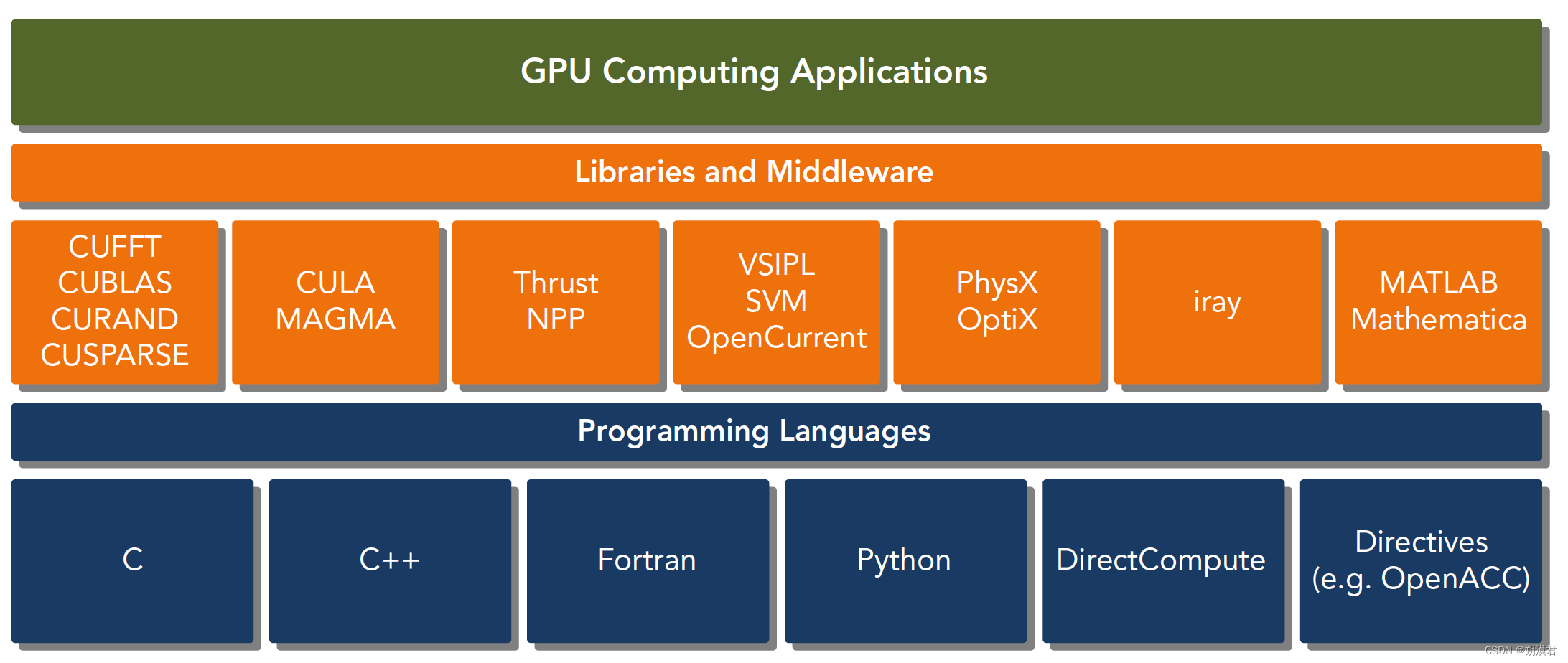
CUDA是建立在Nvidia GPU上的一整套平台，支持多种语言
CUDA的API有两种：
低级API 驱动API 使用困难
高级API 运行时API 使用简单其实现基于驱动API
两种API是互斥的，两者间的函数不能混合调用。
一个CUDA程序
分配GPU内存
拷贝内存到设备
调用CUDA内核函数来执行计算
把计算完成司机拷贝回主机端
内存销毁
其关键点在于内存和线程的管理

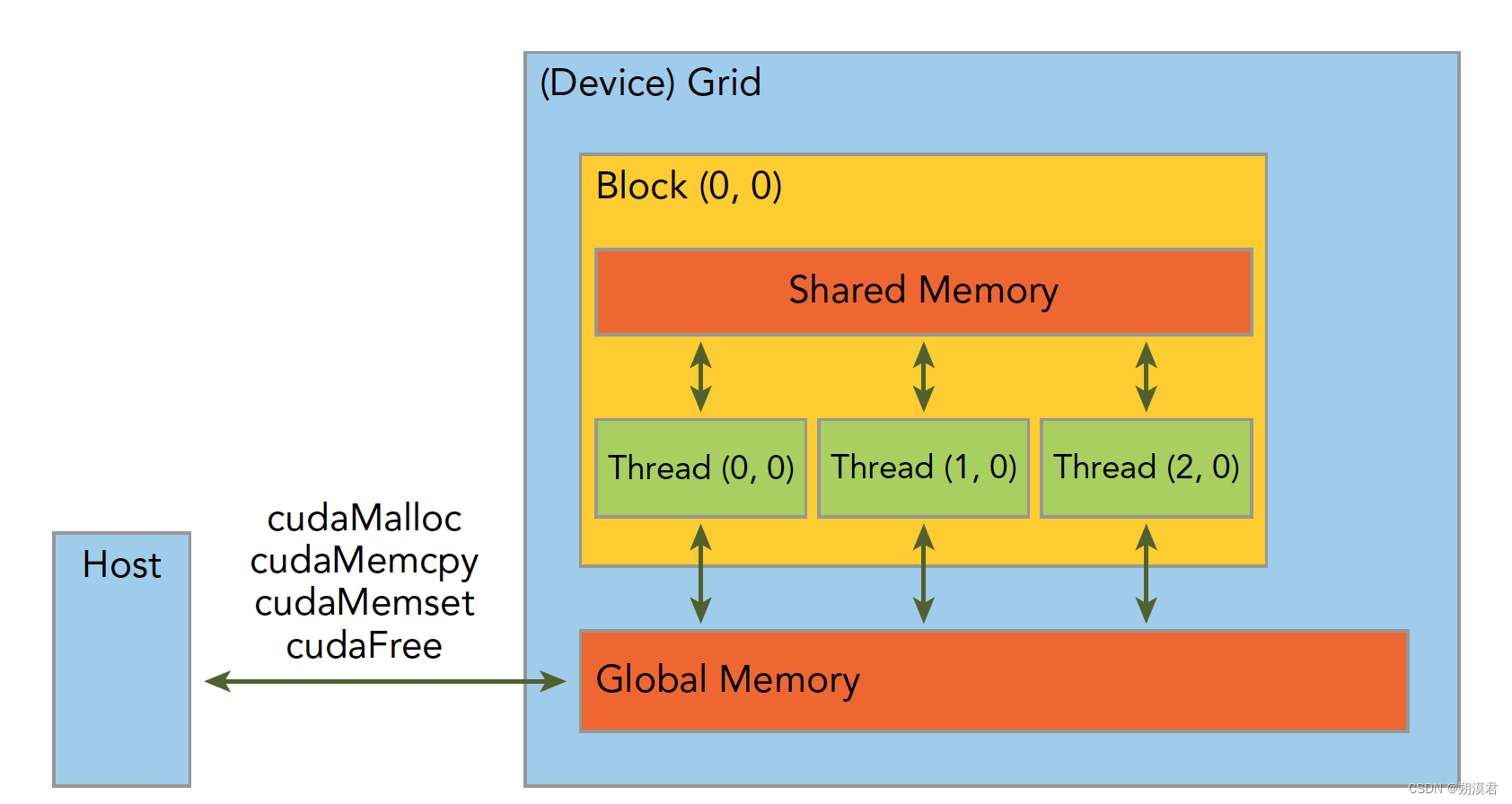
内存
分为共享内存(shared Memory)和全局内存(global Memory)
共享内存在块内，线程间共享
全局内存在grid内共享
- 线程
GPU中的线程层次结构为grid-block-thread
一个核函数只能有一个grid，一个grid可以有很多个块，每个块可以有很多线程。

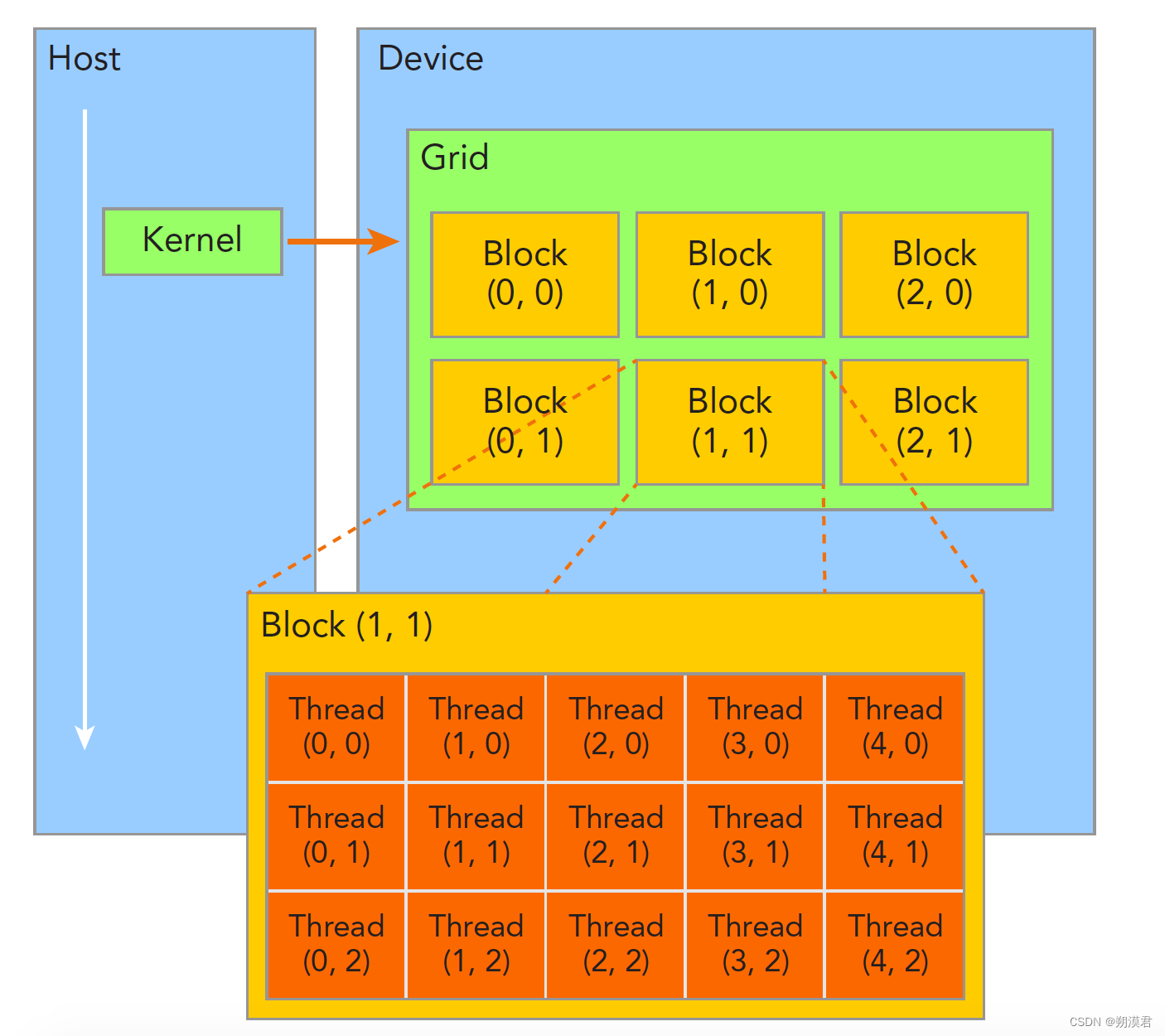
不同块内的线程间不能相互影响，它们是物理隔离的
所有CUDA核函数的启动都是异步的

如何计算线程下标
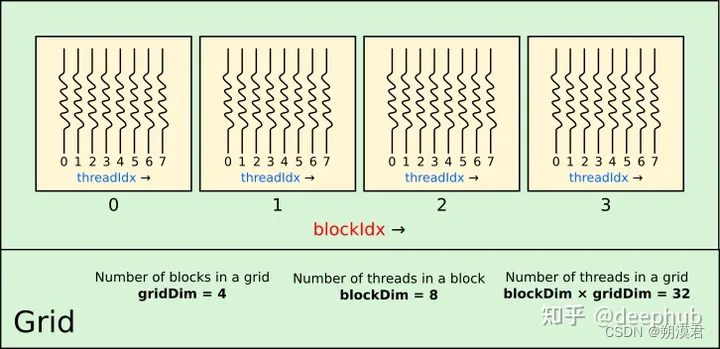
在这里插入图片描述
譬如上图一个grid中有4个block 一个block有8个thread
所以gridDim=4 blockDim=8 线程数=blockDim*gridDim=32
threadIdx.x 取值是0-7

而线程下标如何映射为数组下标呢？一个数组从主机传递到GPU的内存上，现在是并行计算，就不可能用for去逐个获取i值，就得依照以下公式来获取每一个i
i=threadIdx.x+blockDim.x*blockIdx.x
在这里插入图片描述
同时也容易注意到，我们线程是32，但如果数组小于32，比如20，就会有线程溢出的问题，这时该如何解决呢？方案就是，不要做任何事情！

#以python的numba库举例
@cuda.jit
def addArray(a,b,c):
	i = cuda.threadIdx.x+cuda.blockDim.x*cuda.blockIdx.x
	if i<a.size:#线程溢出的部分就不去管它了
		c[i] = a[i]+b[i]
N = 20
a = np.arange(N,dtype=np.float32)
b = np.arange(N,dtype=np.float32)
dev_c = cuda.device_array_like(a)
addArray[4,8](a,b,dev_c)
c = dev_c.copy_to_host()
"""
注：也可以使用i=cuda.grid(1) 1表示获取1维线程索引,2表示2维，3表示3维
"""

因为硬件的限制，GPU并不能运行任意数量的线程和块，通常每个块不能超过1024个线程，一个网格不能超过 $2^{16}-1=65535$ 个块，同时还要考虑内存量。

在numba中硬件限制可以通过cuda.get_current_device()获取
Grid-stride循环
当每个网格的块数超过硬件设置，但显存还有剩余，我们可以使用一个线程来处理数组中的多个元素，这被称为Grid-stride。
就是在核函数里加一个循环来处理多个输入元素。

@cuda.jit
def addArrayGS(a,b,c):
	i_start = cuda.grid(1)
	thread_per_grid = cuda.blockDim.x*cuda.gridDim.x
	for i in range(i_start,a.size,threads_per_grid):
	"""这样设置能够重复利用线程，但并不是一个线程内运行0-a.size-1 而是负责其中的一部分
	比如 当threads_per_grid = 46 a.size=89时
	i_start = 0  i会取值0,46 可以以完整取完0-88的索引
	"""
		c[i]=a[i]+b[i]
threads_per_block = 256
block_per_grid_gs = 32*80
addArrayGS[block_per_grid_gs,threads_per_block](dev_a,dev_b,dev_c)

cuda内核的计算时间
因为GPU和CPU是不通信的，因此在内核启动前后分别调用time.time() 只能获得内核启动需要的时间，而不是计算运行需要的时间。
所以为了获取准确的时间，就得调用cuda.synchronize()函数，这个函数将停止主机执行任何其他代码，直到GPU完成所有核函数。(注：numba是动态编译的，第一调用核函数会计时编译步骤，要获取计算的时间需要二次调用才是准确的)

from time import perf_counter_ns
# Compile and then clear GPU from tasks 
addArray[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_c) 
cuda.synchronize() 

timing = np.empty(101) 
for i in range(timing.size): 
    tic = perf_counter_ns() 
    addArray[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_c) 
    cuda.synchronize() 
    toc = perf_counter_ns() 
    timing[i] = toc - tic 
timing *= 1e-3  # convert to μs 

print(f"Elapsed time: {timing.mean():.0f} ± {timing.std():.0f} μs") 

#  Elapsed time: 201 ± 109 μs 

# Compile and then clear GPU from tasks 
addArrayGS[blocks_per_grid_gs, threads_per_block](dev_a, dev_b, dev_c) 
cuda.synchronize() 

timing_gs = np.empty(101) 
for i in range(timing_gs.size): 
    tic = perf_counter_ns() 
    addArrayGS[blocks_per_grid_gs, threads_per_block](dev_a, dev_b, dev_c) 
    cuda.synchronize() 
    toc = perf_counter_ns() 
    timing_gs[i] = toc - tic 
timing_gs *= 1e-3  # convert to μs 

print(f"Elapsed time: {timing_gs.mean():.0f} ± {timing_gs.std():.0f} μs") 

#  Elapsed time: 178 ± 141 μs

"""对于简单的内核，还可以测量算法的整个过程获得每秒浮点运算的数量。通常以GFLOP/s (giga-FLOP /s)为度量单位。加法操作只包含一个触发器:加法。因此，吞吐量由:"""

#              G * FLOP       / timing in s 
gflops    = 1e-9 * dev_a.size * 1e6 / timing.mean() 
gflops_gs = 1e-9 * dev_a.size * 1e6 / timing_gs.mean() 

print(f"GFLOP/s (algo 1): {gflops:.2f}") 
print(f"GFLOP/s (algo 2): {gflops_gs:.2f}") 

#  GFLOP/s (algo 1): 4.99 
#  GFLOP/s (algo 2): 5.63

一个二维的例子
给定一个值在0-1之间的图像I(x,y) 进行对数校正
$I_z(x,y) = \lambda log_2(1+I(x,y))$

import matplotlib.pyplot as plt 
from skimage import data 
import math 

moon = data.moon().astype(np.float32) / 255. 

fig, ax = plt.subplots() 
im = ax.imshow(moon, cmap="gist_earth") 
ax.set_xticks([]) 
ax.set_yticks([]) 
ax.set_xticklabels([]) 
ax.set_yticklabels([]) 
fig.colorbar(im) 
fig.tight_layout()


# Example 1.5: 2D kernel 
@cuda.jit 
def adjustLog(inp, gain, out): 
    ix, iy = cuda.grid(2) # The first index is the fastest dimension 
    threads_per_grid_x, threads_per_grid_y = cuda.gridsize(2) #  threads per grid dimension 
 
    n0, n1 = inp.shape # The last index is the fastest dimension 
    # Stride each dimension independently 
    for i0 in range(iy, n0, threads_per_grid_y): 
        for i1 in range(ix, n1, threads_per_grid_x): 
            out[i0, i1] = gain * math.log2(1 + inp[i0, i1]) 

#设计二维的线程结构
threads_per_block_2d = (16, 16)  #  256 threads total 
blocks_per_grid_2d = (64, 64) 

moon_gpu = cuda.to_device(moon) 
moon_corr_gpu = cuda.device_array_like(moon_gpu) 

adjustLog[blocks_per_grid_2d, threads_per_block_2d](moon_gpu, 1.0, moon_corr_gpu) 
moon_corr = moon_corr_gpu.copy_to_host() 

fig, (ax1, ax2) = plt.subplots(1, 2) 
ax1.imshow(moon, cmap="gist_earth") 
ax2.imshow(moon_corr, cmap="gist_earth") 
ax1.set(title="Original image") 
ax2.set(title="Log-corrected image") 
for ax in (ax1, ax2): 
    ax.set_xticks([]) 
    ax.set_yticks([]) 
    ax.set_xticklabels([]) 
    ax.set_yticklabels([]) 
fig.tight_layout()