1. 拉格朗日乘子法

拉格朗日乘子法（Lagrange multipliers）是一种寻找多元函数在一组约束下的极值的方法。通过引

入拉格朗日乘子，可将有d个变量与k个约束条件的最优化问题转化为具有d＋k个变量的无约束优化

问题求解。本文希望通过一个直观简单的例子尽力解释拉格朗日乘子法和KKT条件的原理。以包含

一个变量一个约束的简单优化问题为例。

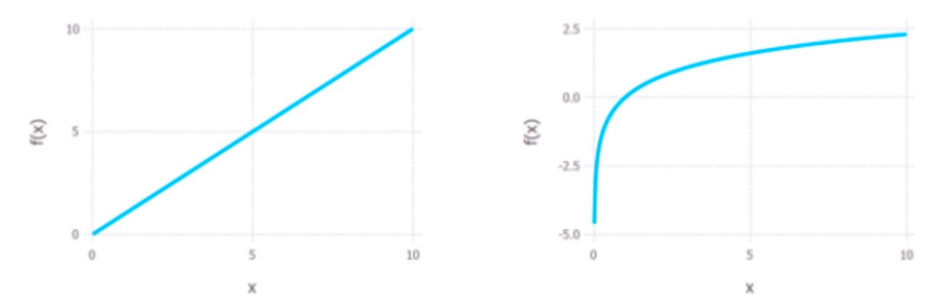
如图所示，我们的目标函数是f(x)＝x2＋4x-1，讨论两种约束条件g(x)：1）在满足x≤-1约

束条件下求目标函数的最小值；2）在满足x≥-1约束条件g(x)下求目标函数的最小值。

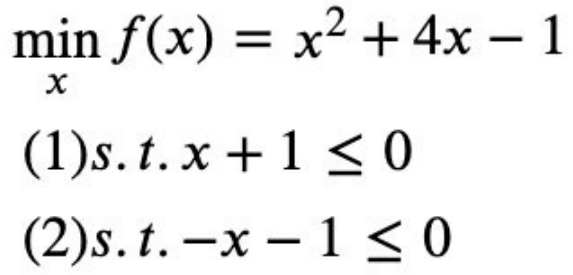
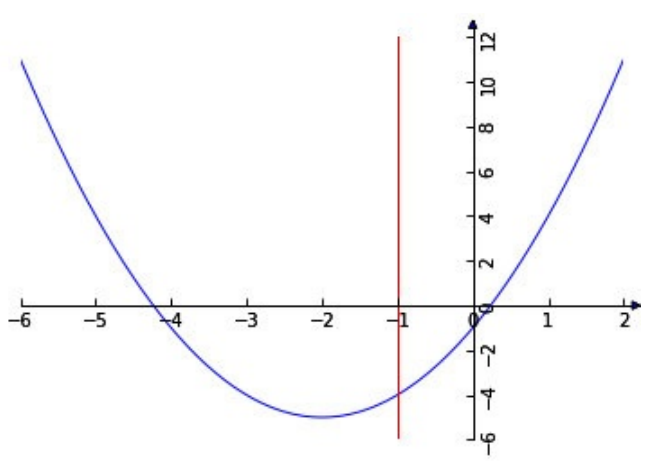
我们可以直观的从图中得到，

对于约束1）使目标值f(x)最小的最优解是x＝-2；

对于约束2）使目标值f(x)最小的最优解是x＝-1。下面我们用拉格朗日乘子来求解这个最优解。

当没有约束的时候，我们可以直接令目标函数的导数为0，求最优值。

可现在有约束，那怎么边考虑约束边求目标函数最优值呢？

最直观的办法是把约束放进目标函数里，由于本例中只有一个约束，所以引入一个朗格朗日乘子

入，构造一个新的函数，拉格朗日函数h(x)，

该拉格朗日函数h(x)最优解可能在g(x)＜0区域中，或者在边界g(x)＝0上，下面具体分析这两种情

况，当g(x)＜0时，也就是最优解在g(x)＜0区域中，对应约束1）x≤-1的情况。此时约束对求目标函

数最小值不起作用，等价于λ＝0，直接通过条件∇f(x＊)＝0，得拉格朗日函数h(x)最优解x＝-2。

当g(x)＝0时，也就是最优解在边界g(x)＝0上，对应约束1）x≥-1的情况。此时不等式约束转换为等

式约束，也就是在λ＞0、约束起作用的情况下，通过求∇f(x＊)＋λ∇g(x＊)＝0，得拉格朗日

函数h(x)最优解x＝-1。

所以整合这两种情况，必须满足λg(x)＝0。因此约束g(x)最小化f(x)的优化问题，可通过引入拉格朗

日因子转化为在如下约束下，最小化拉格朗日函数h（x），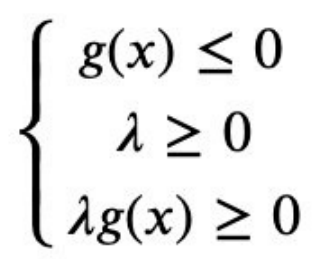

上述约束条件称为KKT条件。

该KKT条件可扩展到多个等式约束和不等式约束的优化问题。

2. Huber Loss

Huber Loss是一个用于回归问题的带参损失函数，优点是能增强平方误差损失函数（MSE，mean

square error）对离群点的鲁棒性。当预测偏差小于ō时，它采用平方误差，当预测偏差大于ō时，

采用的线性误差。相比于最小二乘的线性回归，Huber Loss降低了对离群点的惩罚程度，所以

Huber Loss是一种常用的鲁棒的回归损失函数。

Huber Loss 定义如下：

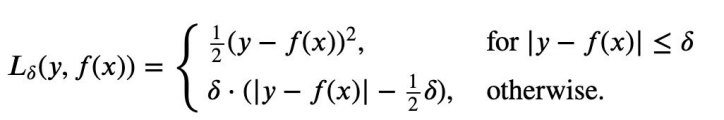
ō是Huber Loss的参数，y是真实值，f(x)是模型的预测值，

通过如上公式，我们可以发现，这个函数对于小一些的(y - f(x))误差函数是二次的，而对大的值误

差函数是线性的。Huber Loss 参数变化图：

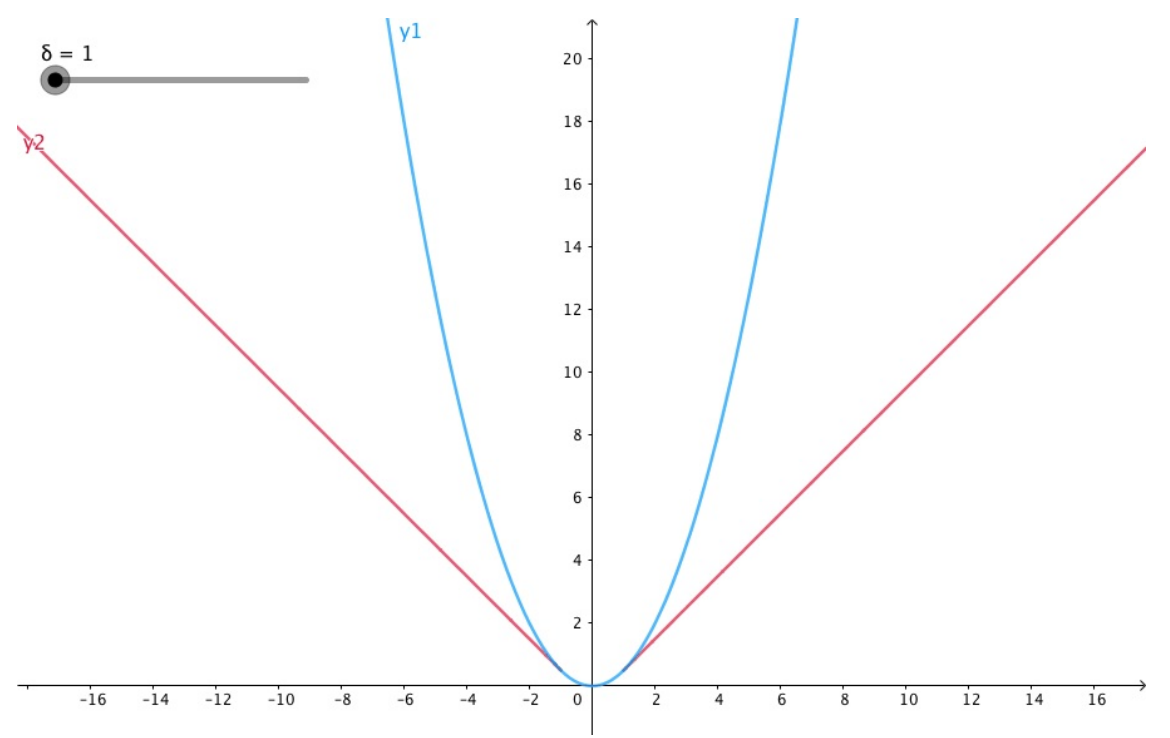
 3. 极大似然函数取对数的原因

①减少计算量

在计算一个独立同分布数据集的联合概率时，如：

其联合概率是每个数据点概率的连乘：

两边取对数则可以将连乘化为连加：

乘法变成加法，从而减少了计算量；同时，如果概率中含有指数项，如高斯分布，能把指数项也化

为求和形式，进一步减少计算量；另外，在对联合概率求导时，和的形式会比积的形式更方便。

②利于结果更好的计算

但其实可能更重要的一点是，因为概率值都在［0，1］之间，因此，概率的连乘将会变成一个很小

的值，可能会引起浮点数下溢，尤其是当数据集很大的时候，联合概率会趋向于0，非常不利于之

后的计算。

③取对数并不影响最后结果的单调性

因为相同的单调性，它确保了概率的最大对数值出现在与原始概率函数相同的点上。因此，可以用

更简单的对数似然来代替原来的似然。