一、问题描述:
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
二、解题思路:
- 整体思路就是模拟螺旋遍历矩阵的过程,依次遍历外围边界的元素,并将其按顺序存入结果列表中。这样就可以实现将二维矩阵按螺旋顺序转换为一维数组的效果。
- 解题思路:
①定义变量 l 来表示当前层,以及变量 n 和 m 分别表示矩阵的行数和列数。定义 mid = Math.min(n, m) / 2,作为遍历层数的上限。
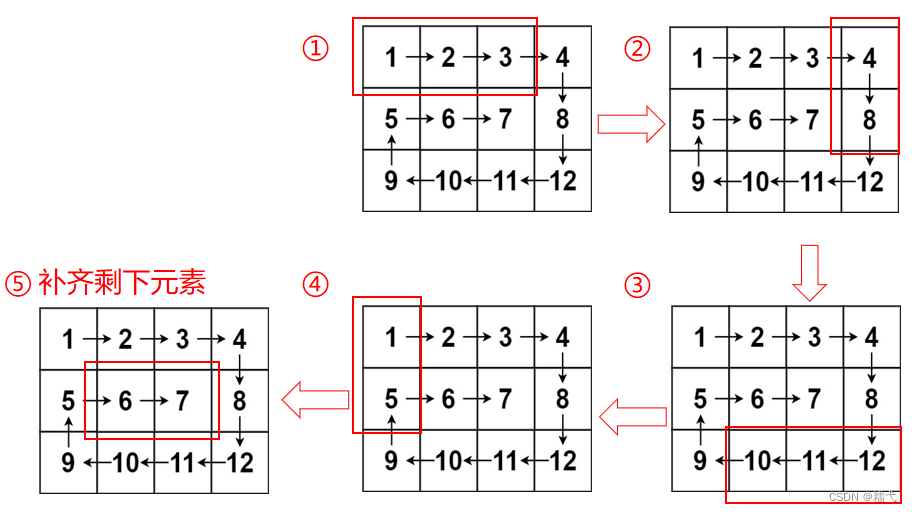
②接下来,通过一个 while 循环,不断遍历矩阵的外围边界,按照螺旋的顺序将元素加入结果列表中。具体的遍历顺序为:从左到右、从上到下、从右到左、从下到上,分别对应四个边界。
③在遍历过程中会不断更新当前层 l 的值,并且在遍历完成后,如果矩阵的行或列是奇数,还会补齐中心点周围的元素。
三、代码示例:
//时间复杂度为O(n*m)
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> res = new ArrayList<>(); // 创建一个用于存放结果的列表
int l = 0; // 定义一个变量 l 来表示当前层
int n = matrix.length; // 获取矩阵的行数
int m = matrix[0].length; // 获取矩阵的列数
int mid = Math.min(n, m) / 2; // 计算行数和列数的较小值除以2,作为遍历层数的上限
while (l < mid) { // 当 l 小于 (行数和列数中的较小值/2) 时,继续循环
for (int j = l; j < m - l - 1; j++)
res.add(matrix[l][j]); // 添加元素到结果列表,第 l 行
for (int j = l; j < n - l - 1; j++)
res.add(matrix[j][m - l - 1]); // 添加元素到结果列表,最后 m-l-1 列
for (int j = m - l - 1; j > l; j--)
res.add(matrix[n - l - 1][j]); // 添加元素到结果列表,最后 n-l-1 行
for (int j = n - l - 1; j > l; j--)
res.add(matrix[j][l]); // 添加元素到结果列表,第 l 列
l++; // 继续下一层
}
if (Math.min(n, m) % 2 != 0) { // 如果矩阵的行或列是奇数,需要补齐中心点周围的元素
if (n > m) { // 如果行数大于列数
for (int i = mid; i < mid + n - m + 1; i++)
res.add(matrix[i][mid]); // 补齐中心点上方的元素
} else { // 如果列数大于行数
for (int i = mid; i < mid + m - n + 1; i++)
res.add(matrix[mid][i]); // 补齐中心点左侧的元素
}
}
return res; // 返回结果列表
}
}
- 时间复杂度分析:按照顺时针螺旋顺序遍历二维矩阵,并将遍历结果存储在一个列表中。矩阵中的每个元素都要被访问一次。因此时间复杂度为O(n*m)。
四、补充与总结:
建议先做一下59题,该题中矩阵的行和列是相等的。
- 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
-
解题思路:
①创建一个 n x n 的二维数组来表示矩阵,初始化为全0。
②定义变量 l 作为当前层的索引,初始值为 0。
③定义变量 a 用来填充矩阵,初始值为 1。
④在每一层循环中,按照顺时针的顺序填充矩阵的元素:
(1)从左到右填充当前层的上方一行。
(2)从上到下填充当前层的右侧一列。
(3)从右到左填充当前层的下方一行。
(3)从下到上填充当前层的左侧一列。
(4)每填充一个位置,就将 a 的值加一。
⑤继续进行下一层的填充,直到遍历完所有层。 -
代码示例
class Solution {
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n]; // 创建一个 n x n 的矩阵
int l = 0; // 定义一个变量 l 来表示当前层
int a = 1; // 初始值为 1,用来填充矩阵
while (l < n / 2) { // 当 l 小于 n/2 时,继续循环
// 填充当前层的上方一行
for (int j = l; j < n - l - 1; j++)
matrix[l][j] = a++;
// 填充当前层的右侧一列
for (int j = l; j < n - l - 1; j++)
matrix[j][n - l - 1] = a++;
// 填充当前层的下方一行
for (int j = n - l - 1; j > l; j--)
matrix[n - 1 - l][j] = a++;
// 填充当前层的左侧一列
for (int j = n - l - 1; j > l; j--)
matrix[j][l] = a++;
l++; // 继续下一层
}
if (n % 2 == 1) // 如果 n 为奇数,填充中心点的元素
matrix[l][l] = a;
return matrix; // 返回填充好的矩阵
}
}