一、选择题
01.一个算法应该是( B ).
A.程序 B.问题求解步骤的描述
C.要满足五个基本特性 D.A和C
02.某算法的时间复杂度为O(n²),则表示该算法的( C )。
A,问题规模是n² (默认都是n) B.执行时间等于n² <=k*n²
C.执行时间与n²成正比 D.问题规模与n²成正比
解析:算法时间复杂度:O(F(n))意味着算法在任何情况下,规模为n时,所花费的时间<=k*F(n)
03.若某算法的空间复杂度为O(1),则表示该算法( B )。
A,不需要任何辅助空间 B.所需辅助空间大小与问题规模n无关
C.不需要任何空间 D.所需空间大小与问题规模n无关
04.下列关于时间复杂度的函数中,时间复杂度最小的是( D ).
05.以下算法的时间复杂度为( D ).
void fun(int n){ //n作为参数
int i=1;while(i<=n)
i=i*2; //核心运算}
![]()
解析:核心操作是i=i*2;判断运算次数 ,即1*2*2*2乘多少次是n (2的几次方是n)
06.有以下算法,其时间复杂度为( C ).
void fun (int n){
int i=0;
while(i*i*i<=n)
i++; //i通过++操作往后推进,是核心操作}
![]()
解析:核心运算是i++,i*i*i仅用于逻辑判断,并没有“推进i”
当i*i*i>n时,则停止增加 即i = n开三次方
07.程序段如下:
for(i=n-1;i>1;i--)
for(j=1;j<i;j++)
if(A[j]>A[j+1]) //满足条件执行if
A[j]与A[j+1]对换;
其中n为正整数,则最后一行语句的频度在最坏情况下是( D )。![]()
解析:冒泡排序的算法代码,所有相邻元素都为逆序时,最后一行的语句每次都会执行
08.下列程序段的时间复杂度为( A )。
if(n>=0){
for (int i=0;i<n;i++)
for(int j=0;j<n;j++)
printf("输入数据大于或等于零\n");
}
else{
for(int j=0;j<n;j++)
printf("输入数据小于零\n");
![]()
09.以下算法中加下画线的语句的执行次数为( A )。 m++的执行次数
int m=0,i,j;
for(i=1;i<=n;i++)
for(j=1;j<=2*i;j++)
m++;
A. n(n+1) B.n C. n+1 D. n²
10.下列函数代码的时间复杂度是( C )。
int Func(int n){
if(n==1)return 1;
elsereturn 2* Func(n/2)+n;
![]()
11.【2011统考真题】设n是描述问题规模的非负整数,下列程序段的时间复杂度是( A )
x=2; //初值
while(x<n/2) //结束条件x=2*x; //执行操作
![]()
解析:x=2*2*2*....乘多少次2达到n
12.【2012统考真题】求整数n(n≥0)的阶乘的算法如下,其时间复杂度是( B )。
int fact(int n){
if(n<=1)return 1;
return n*fact (n-1); //递归程序
![]() “
“
解析:程序就是一个递归,整个程序的基础操作只有递归处有乘法,一次递归是一次乘法运算,值为n的情况下递归嵌套n次
13.【2014统考真题】下列程序段的时间复杂度是( C )。
count=0;
for(k=1;k<=n;k*=2)for(j=1;j<=n;j++)
count++;
![]()
解析:第一层:k的取值分别是1,2,4,8...一直到n:log2n次循环
第二层:无论k的取值是多少,第二层都是自加n次
14.【2017统考真题】下列函数的时间复杂度是( B ).
int func (int n){
int i=0,sum=0;
while(sum<n)sum += ++i;
return i;
)
![]()
解析:核心操作:sum+=++i; sum的变化过程:0+1+2+3....+i ,当sum<n时跳出循环,判断i加了几次,求和公式为sum=i*(i-1)/2<n,根据数量级可以把左边看成i²,即i²<n ,所以i=n的二分之一次方
15.【2019统考真题】设n是描述问题规模的非负整数,下列程序段的时间复杂度是( B )。
x=0;
while (n>=(x+1)*(x+1))x=x+1;
![]()
解析:(x+1)²<=n ,根据同阶数量级可以看成x²<n 即x趋向于根号n
16.【2022统考真题】下列程序段的时间复杂度是( B )。
int sum=0;
for(int i=l;i<n;i*=2)
for(int j=0;j<i;j++)
sum++;
![]()
解析:求出sum++的执行次数
第一层:i=1,2,4,8...2的k次方
第二层:j<i,所以j有0~i-1个
1+2+3+....+2的k次方 = 2的k+1次方-1<2n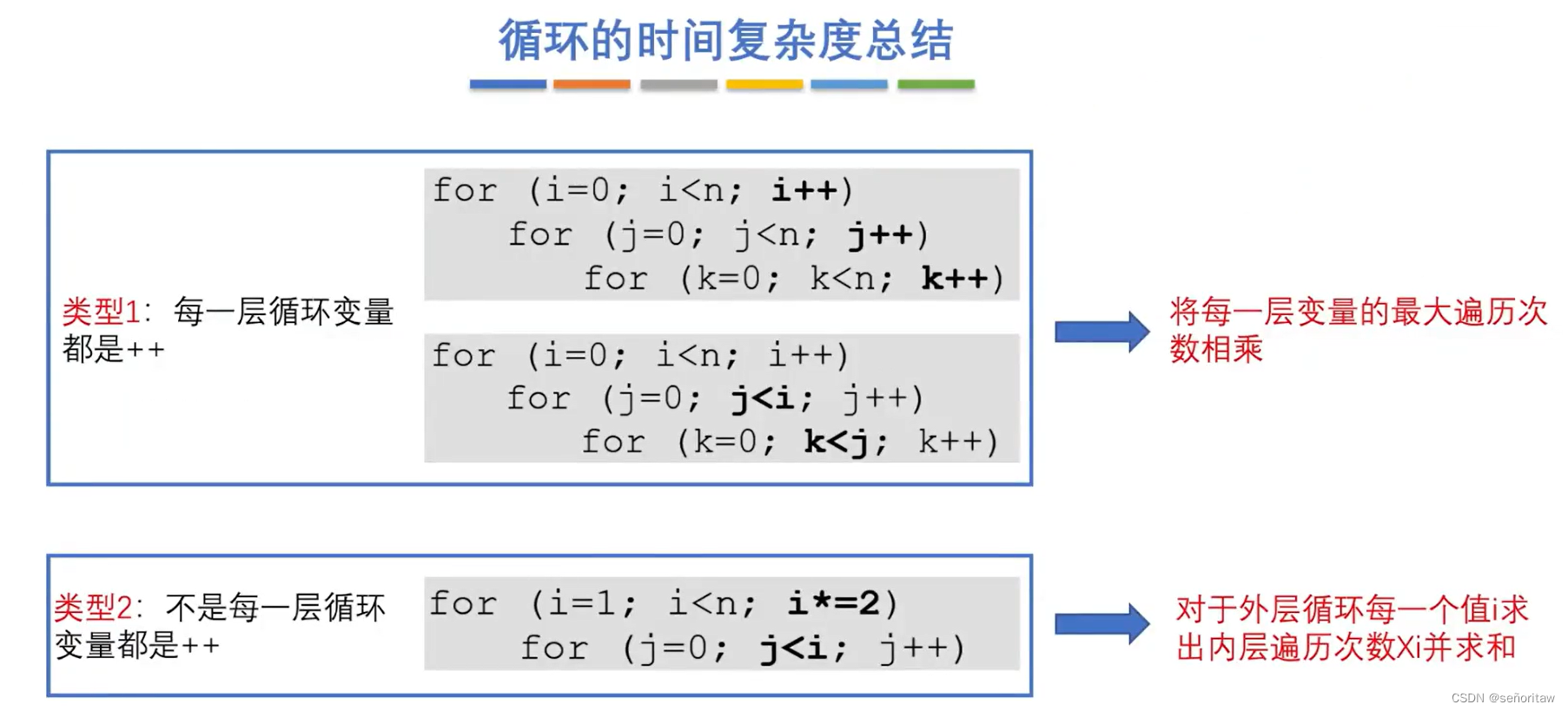
二、综合应用题
01.分析以下各程序段,求出算法的时间复杂度。
① i=1;k=0;
while(i<n-1){
k=k+10*i;i++;
② y=0;
while((y+1)*(y+1)<=n)
y=y+1;
③ for(i=0;i<n;i++)
for(j=0;j<m;j++)
a[i][j]=0;
①基本语句k=k+10*i共执行了n-2次,所以T(n)= O(n)。
②设循环体共执行t次,每循环一次,循环变量y加1,最终t=y。故t²≤n,得T(n)=O(n1/2)。
③内循环执行m次,外循环执行n次,根据乘法原理,共执行了mxn次,故T(m, n)=O(mxn)。