线弹性材料本构模型
- 对于多数材料而言,在微小变形的假设下,会满足线弹性理论,数学可以表示为:
σ i j = C i j k l ε k l = E 1 + ν ( ε i j + ν 1 − 2 ν ε k k δ i j ) \begin{align*} \sigma_{ij}&=C_{ijkl}\varepsilon_{kl}\\ &=\frac{E}{1+\nu}(\varepsilon_{ij}+\frac{\nu}{1-2\nu}\varepsilon_{kk}\delta_{ij}) \end{align*} σij=Cijklεkl=1+νE(εij+1−2ννεkkδij)
C i j k l C_{ijkl} Cijkl是材料的弹性刚度,该四阶张量共有81个分量( i 、 j 、 k 、 l i、j、k、l i、j、k、l皆为1到3的整数)
-
考虑任意一个计算域内微小元素的力平衡、力矩平衡以及在微小变形理论中应变的计算得:
σ i j = σ j i ε k l = 1 2 ( ∂ u k ∂ x l + ∂ u l ∂ x k ) ε k l = ε l k → C i j k l = C j i k l = C i j l k \begin{gather*} \sigma_{ij}=\sigma_{ji}\\ \varepsilon_{kl}=\frac{1}{2}(\frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k})\\ \varepsilon_{kl}=\varepsilon_{lk}\\ \rightarrow \quad C_{ijkl}=C_{jikl}=C_{ijlk} \end{gather*} σij=σjiεkl=21(∂xl∂uk+∂xk∂ul)εkl=εlk→Cijkl=Cjikl=Cijlk
可知刚度矩阵具有对称关系,故刚度矩阵元素中独立元素个数减少为36个。采用张量标记法Voigt标记刚度矩阵:
[ σ 1 σ 2 σ 3 σ 4 σ 5 σ 6 ] = E ( 1 + ν ) ( 1 − 2 ν ) [ 1 − ν ν ν 0 0 0 ν 1 − ν ν 0 0 0 ν ν 1 − ν 0 0 0 0 0 0 1 − 2 ν 2 0 0 0 0 0 0 1 − 2 ν 2 0 0 0 0 0 0 1 − 2 ν 2 ] [ ε 1 ε 2 ε 3 2 ε 4 2 ε 5 2 ε 6 ] \begin{bmatrix} \sigma_1\\ \sigma_2\\ \sigma_3\\ \sigma_4\\ \sigma_5\\ \sigma_6 \end{bmatrix}=\frac{E}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1-\nu & \nu & \nu & 0 & 0 & 0\\ \nu & 1-\nu & \nu & 0 & 0 & 0\\ \nu & \nu & 1-\nu & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1-2\nu}{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1-2\nu}{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1-2\nu}{2} \end{bmatrix} \begin{bmatrix} \varepsilon_1\\ \varepsilon_2\\ \varepsilon_3\\ 2\varepsilon_4\\ 2\varepsilon_5\\ 2\varepsilon_6 \end{bmatrix} σ1σ2σ3σ4σ5σ6 =(1+ν)(1−2ν)E 1−ννν000ν1−νν000νν1−ν00000021−2ν00000021−2ν00000021−2ν ε1ε2ε32ε42ε52ε6 -
为方便参数设定,采用参数替换
- 拉梅常数
λ = E ν ( 1 + ν ) ( 1 − 2 ν ) \lambda=\frac{E\nu}{(1+\nu)(1-2\nu)} λ=(1+ν)(1−2ν)Eν - 剪切模量
μ = E 2 ( 1 + ν ) \mu=\frac{E}{2(1+\nu)} μ=2(1+ν)E - 刚度矩阵
C = [ λ + 2 μ λ λ 0 0 0 λ λ + 2 μ λ 0 0 0 λ λ λ + 2 μ 0 0 0 0 0 0 μ 0 0 0 0 0 0 μ 0 0 0 0 0 0 μ ] C=\begin{bmatrix} \lambda+2\mu & \lambda & \lambda & 0 & 0 & 0\\ \lambda & \lambda+2\mu & \lambda & 0 & 0 & 0\\ \lambda & \lambda & \lambda+2\mu & 0 & 0 & 0\\ 0 & 0 & 0 & \mu & 0 & 0 \\ 0 & 0 & 0 & 0 & \mu & 0 \\ 0 & 0 & 0 & 0 & 0 & \mu \end{bmatrix} C= λ+2μλλ000λλ+2μλ000λλλ+2μ000000μ000000μ000000μ
- 拉梅常数
线弹性材料本构的umat编写
SUBROUTINE UMAT(
C **** 参数列 ***********************************************C
1 STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
2 RPL,DDSDDT,DRPLDE,DRPLDT,
3 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
4 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
5 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC
C **** 宣告参数***********************************************C
INCLUDE`ABA_PARAM.INC`
C------------------------------------------------------------C
CHARACTER*80 CMNAME
DIMENSION STRESS(NTENS),STATEV(NSTATV),
1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3)
4 JSTEP(4)
C------------------------------------------------------------C
REAL*8 E, NU, MU, LAM, MU2
INTEGER*4 I, J
C **** 材料模型主程序***********************************************C
C **** 材料使用错误,停止分析
IF (NTENS .EQ. 1) THEN
WRITE(7,*) `错误:本线弹性模型不支持一维元素`
CALL XIT
ENDIF
C **** 材料刚度系数归零
DO I = 1,NTENS
DO J = 1,NTENS
DDSDDE(I,J) = 0.D0
ENDDO
ENDDO
C **** 材料参数读取与计算
E = PROPS(1)
NU = PROPS(2)
MU = E/(2.D0+2.DO*NU)
LAM= MU*NU/(0.5D.0-NU)
C **** 剪应力和刚度矩阵
DO J = 1,NSHR
I = J+NDI
DDSDDE(I,I) = MU
STRESS(I) = STRESS(I)+ MU*DSTRAN(I)
C **** 法向应力和刚度矩阵
MU2 = 2.D0*MU
DO I = 1,NDI
DO J = 1,NDI
DDSDDE(I,J) = LAM
STRESS(I) = STRESS(I)+ LAM*DSTRAN(J)
ENDDO
DDSDDE(I,I) = LAM+ MU2
STRESS(I) = STRESS(I) + MU2*DSTRAN(I)
ENDDO
C------------------------------------------------------------C
RETURN
END SUBROUTINE UMAT
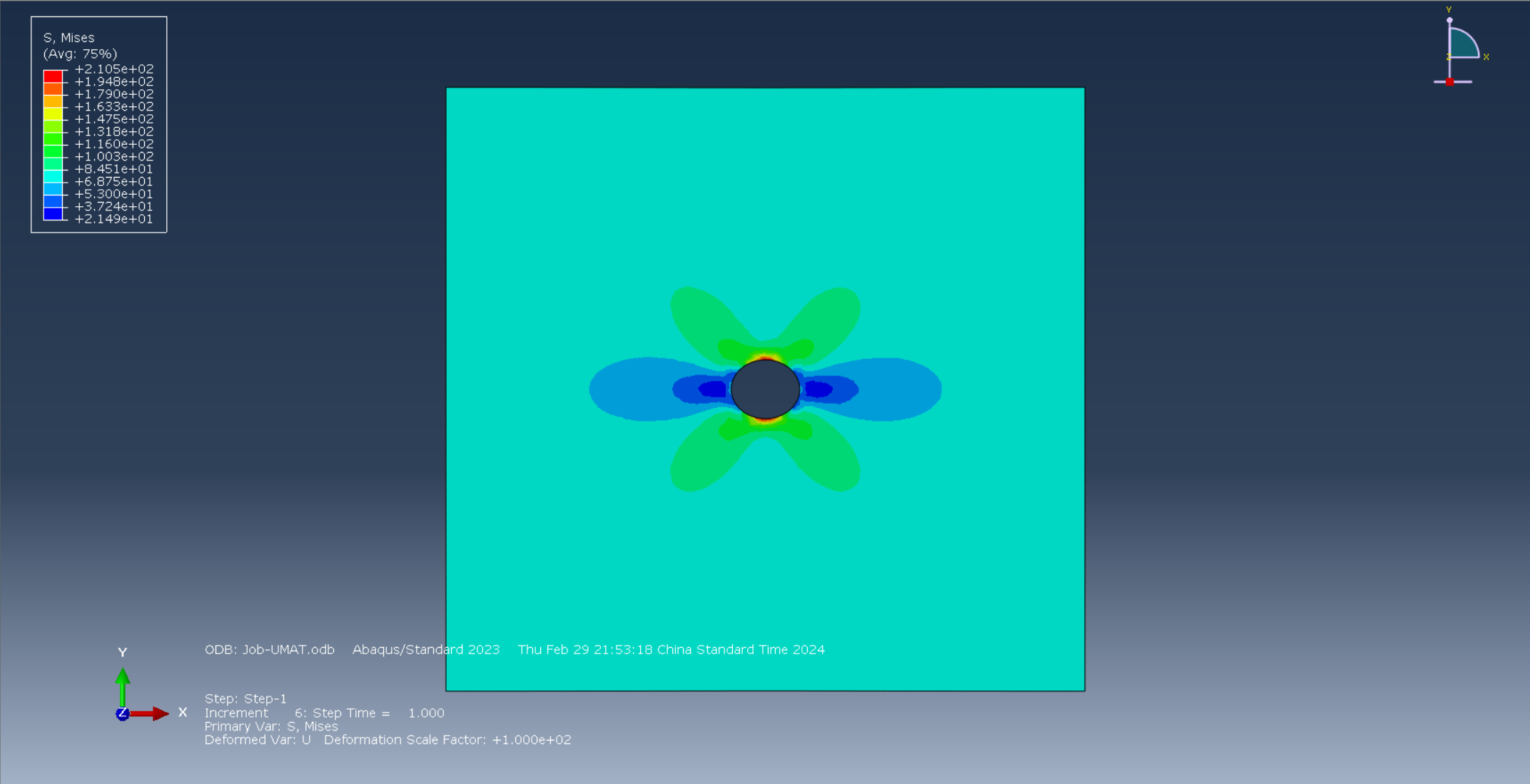
UMAT应用案例
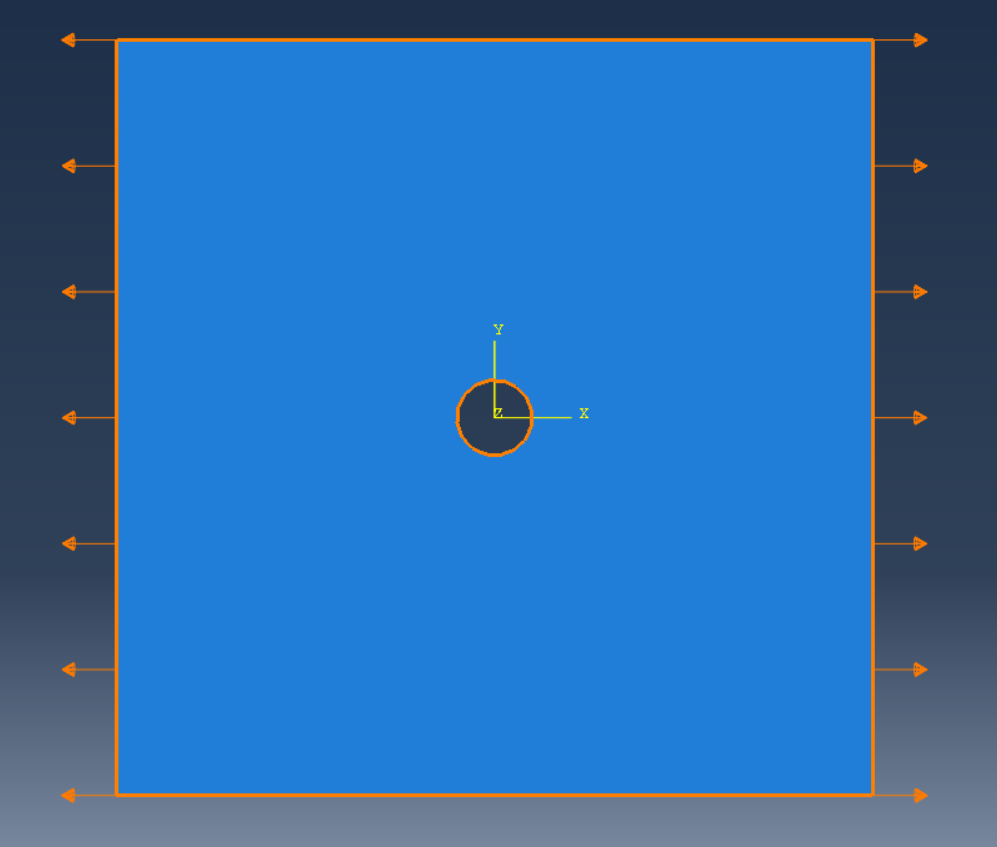
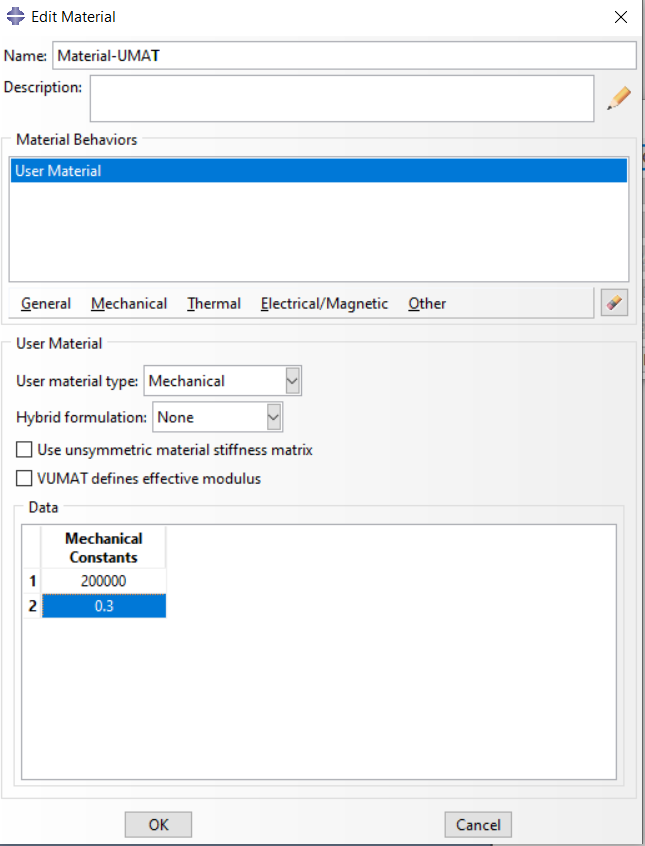
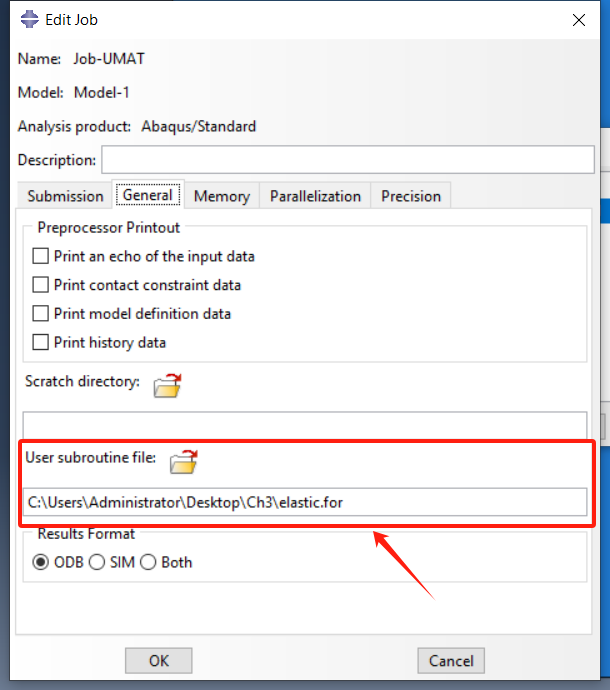
- 假设一线弹性材料厚板,大小为 500 m m × 500 m m m 500mm\times 500mmm 500mm×500mmm,在中心挖一半径为 25 m m 25mm 25mm的圆,并在板两侧施加 0.1 m m 0.1mm 0.1mm的位移,已知材料的弹性模量 E = 200 G P a E=200GPa E=200GPa,泊松比 ν = 0.3 \nu=0.3 ν=0.3。
**
ZWT——朱-王-唐本构模型:
**

如果你喜欢以上内容,或者对Abaqus学习有兴趣,欢迎收藏关注,博主将持续更新。你的关注、收藏是我持续创作的动力!