七大排序算法(一篇文章梳理)

news2024/11/18 15:37:54

一、引言

排序算法是计算机科学中不可或缺的一部分，它们在数据处理、数据库管理、搜索引擎、数据分析等多个领域都有广泛的应用。排序算法的主要任务是将一组数据元素按照某种特定的顺序（如升序或降序）进行排列。本文将对一些常见的排序算法进行详细的介绍和分析，包括冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序等。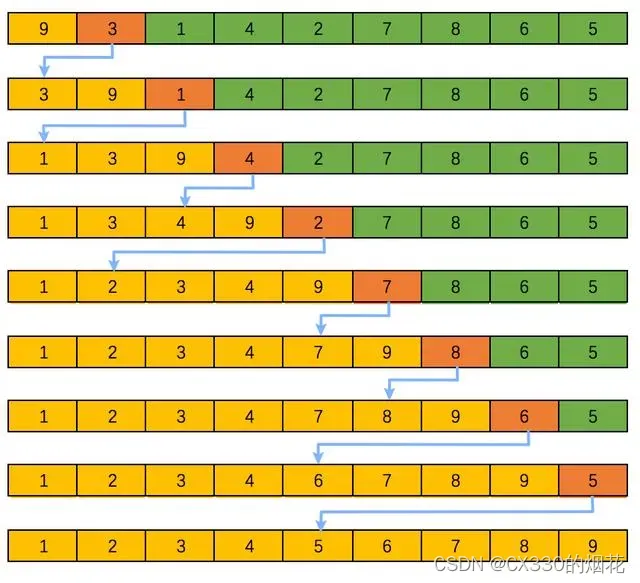

二、排序算法的分类

排序算法大致可以分为以下几类：

1 比较排序

基于比较的排序算法通过比较元素的大小来决定它们的顺序。常见的比较排序算法有冒泡排序、选择排序、插入排序、归并排序、快速排序等。

2 非比较排序

非比较排序算法不依赖于元素之间的比较，而是利用一些特定的属性或规则来排序。常见的非比较排序算法有计数排序、基数排序、桶排序等。

3 稳定排序

稳定排序算法在排序过程中，如果两个元素相等，它们在排序后的相对位置不会改变。常见的稳定排序算法有冒泡排序、插入排序、归并排序等。

4 不稳定排序

不稳定排序算法在排序过程中，如果两个元素相等，它们在排序后的相对位置可能会改变。常见的不稳定排序算法有选择排序、快速排序、堆排序等。

三、常见排序算法详解

1 冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法，它重复地遍历待排序的序列，一次比较两个相邻的元素，如果它们的顺序错误就把它们交换过来。遍历序列的工作是重复地进行直到没有再需要交换，也就是说该序列已经排序完成。

时间复杂度：O(n^2)

空间复杂度：O(1)

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

2 选择排序（Selection Sort）

选择排序是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

时间复杂度：O(n^2)

空间复杂度：O(1)

def selection_sort(arr):
    for i in range(len(arr)):
        min_index = i
        for j in range(i+1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr

3 插入排序（Insertion Sort）

插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

时间复杂度：O(n^2)（最坏情况）

空间复杂度：O(1)

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

4 希尔排序（Shell Sort）

希尔排序是插入排序的一种更高效的改进版本，也称为缩小增量排序。它通过将待排序序列划分为若干个子序列，先对子序列进行直接插入排序，然后逐步合并子序列，最后进行一次全体记录的直接插入排序。

时间复杂度：O(n^1.3)（平均情况）

空间复杂度：O(1)

def shell_sort(arr):
    size = len(arr)
    gap = size // 2
    while gap > 0:
        for i in range(gap, size):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2
    return arr

5 归并排序（Merge Sort）

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。它将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

时间复杂度：O(nlogn)

空间复杂度：O(n)

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    merged = []
    left_index = 0
    right_index = 0
    while left_index < len(left) and right_index < len(right):
        if left[left_index] < right[right_index]:
            merged.append(left[left_index])
            left_index += 1
        else:
            merged.append(right[right_index])
            right_index += 1
    merged.extend(left[left_index:])
    merged.extend(right[right_index:])
    return merged

6 快速排序（Quick Sort）

快速排序是一种高效的排序算法，采用分治策略。它选择一个元素作为基准（pivot），将序列分为两部分，一部分小于基准，一部分大于基准，然后递归地对这两部分进行排序。

时间复杂度：O(nlogn)（平均情况）

空间复杂度：O(logn)（递归调用栈）

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

7 堆排序（Heap Sort）

堆排序是一种基于堆数据结构的排序算法，它利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

时间复杂度：O(nlogn)

空间复杂度：O(1)

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[i] < arr[left]:
        largest = left

    if right < n and arr[largest] < arr[right]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # Build a maxheap
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # One by one extract elements
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

    return arr