1、45.跳跃游戏 II

🦄解题思路：

这题还是比【55.跳跃游戏】难一些的。第一个版本只是说，求跳跃的范围，覆盖到了终点即可。这题则是，能保证覆盖范围到达终点，求的是最少跳几次，跳到终点。

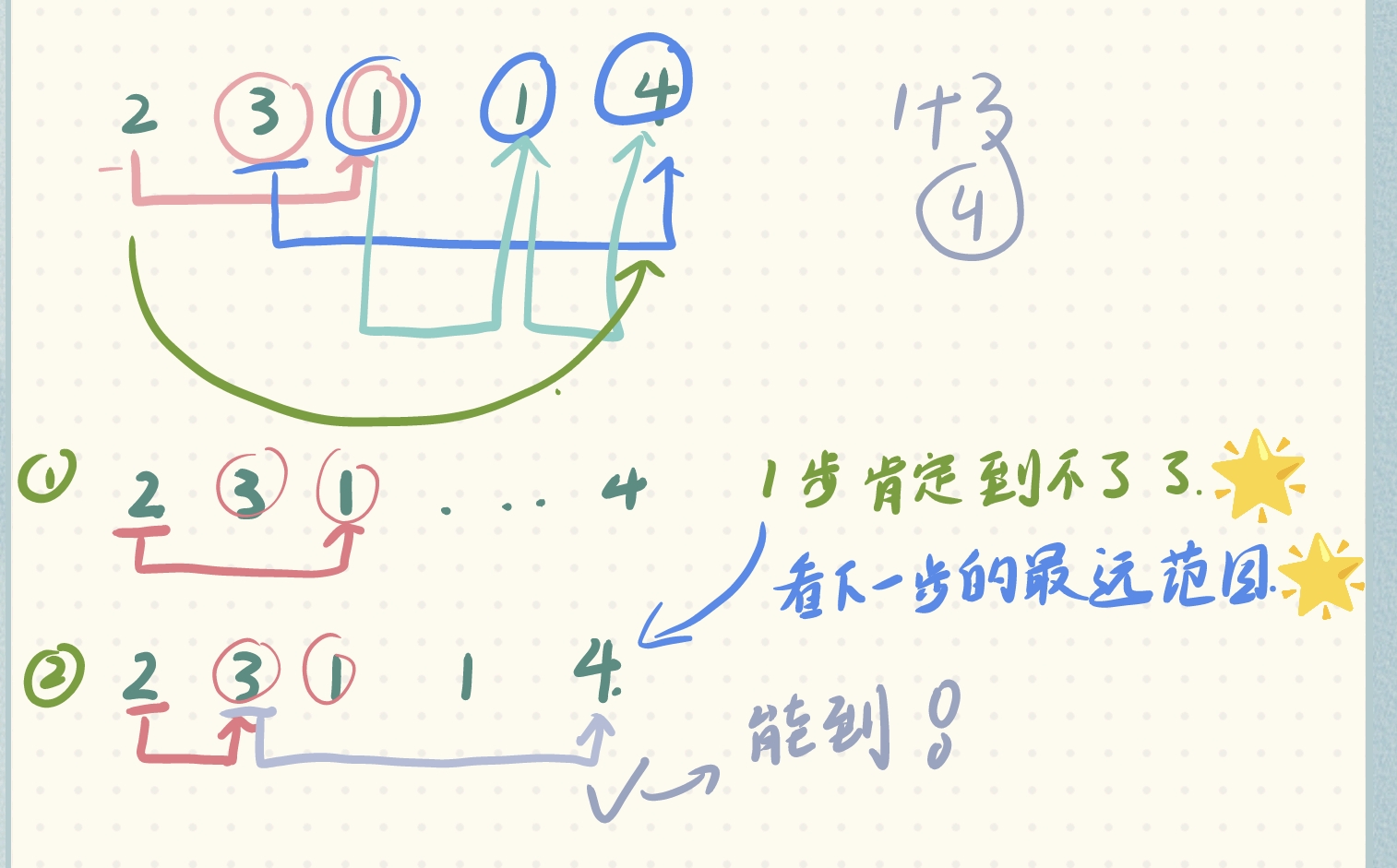
这题的话也是偏直觉，最好能一步到就好，一步到不了，两步能到吗？两步还到不了，三步呢？听起来是不是还挺简单的？但是实现起来，还是有一些需要考虑的。

❌错误代码和分析1：

class Solution {
public:
    int jump(vector<int>& nums) {
        int cover_now = 0;//当前元素所能cover的最远范围
        int cover_next_max = 0;//如果多跳一步，下一步将cover的最远范围
        int cnt = 0;//跳跃步数
        if(nums.size() == 1) return 0;
        for (int i = 0; i <= cover_next_max; i++){
            cover_now = i + nums[i];
            if(cover_now >= nums.size()-1){
                return ++cnt;
            }
            cover_next_max = max(cover_next_max, cover_now);
            ++cnt;
        }
        return cnt;
    }
};

明白了大致思路，但是实现起来还是有问题，我们再来捋一下思路。

• 首先要明白什么是now_cover：这个now指的是当前跳了cnt步，最远的覆盖范围！
• 什么是next_cover_max:在现在cnt的基础上+1，也就是多跳一步（cnt++肯定就是已经确定，跳当前cnt步，肯定到不了终点)，能到达的最远范围。
• 而我们也知道，从当前位置，可以有多种跳跃选择，都是算再跳一步，那么怎么选择，才能让跳跃这一步，能在跳到的新位置能直接跳到终点或能跳的更远；这就是我们要求的下一步的最远距离：再跳一次，可以覆盖的最远范围：next_cover_max
• 而什么时候需要跳呢，也就是说，当当前遍历位置，达到now_cover了，也就是说，跳当前的cnt步，无论如何都到达不了终点；那么这个时候cnt++说明需要多跳一步，跳的一个新位置，看看能不能从这个新位置到达终点。
  
  ✅正确代码：

class Solution {
public:
    int jump(vector<int>& nums) {
        int cover_now = 0;//当前元素所能cover的最远范围
        int cover_next_max = 0;//如果多跳一步，下一步将cover的最远范围
        int cnt = 0;//跳跃步数
        if(nums.size() == 1) return 0;
        for (int i = 0; i <= nums.size()-1; i++){
            cover_next_max = max(cover_next_max, i + nums[i]); //更新多跳一步，从新位置可以到达的最远范围
            if(cover_next_max >= nums.size()-1) return ++cnt; //若可以到达，说明的确只需要跳一步就到达终点，返回当前cnt++即可
            if(i == cover_now){ //说明跳当前cnt步，无论如何都到不了终点
                cnt ++; //必须至少多跳一步
                cover_now = cover_next_max;  //更新当前cnt所能覆盖的最远范围
            }
        }
        return cnt;
    }
};