一、一个粒子的模拟

规定一个物体在某一个时刻的速度和位置，如何解出某个时间之后它会出现在哪里
下图要求模拟一个粒子在速度场中要如何运动

速度场中，在任何一个位置，我们都有它的速度
写出来相当于是常微分方程

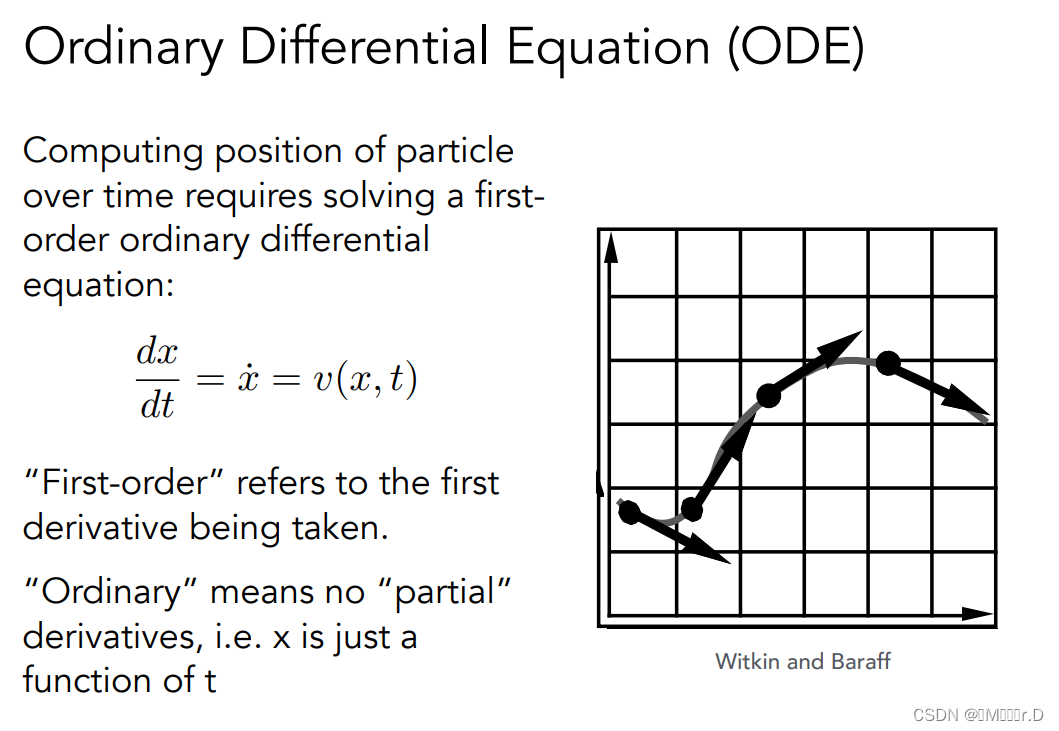
我们知道速度，想知道任何一个时刻的位置
我们会给出起始位置，以及需要的时间，我们怎么解呢？

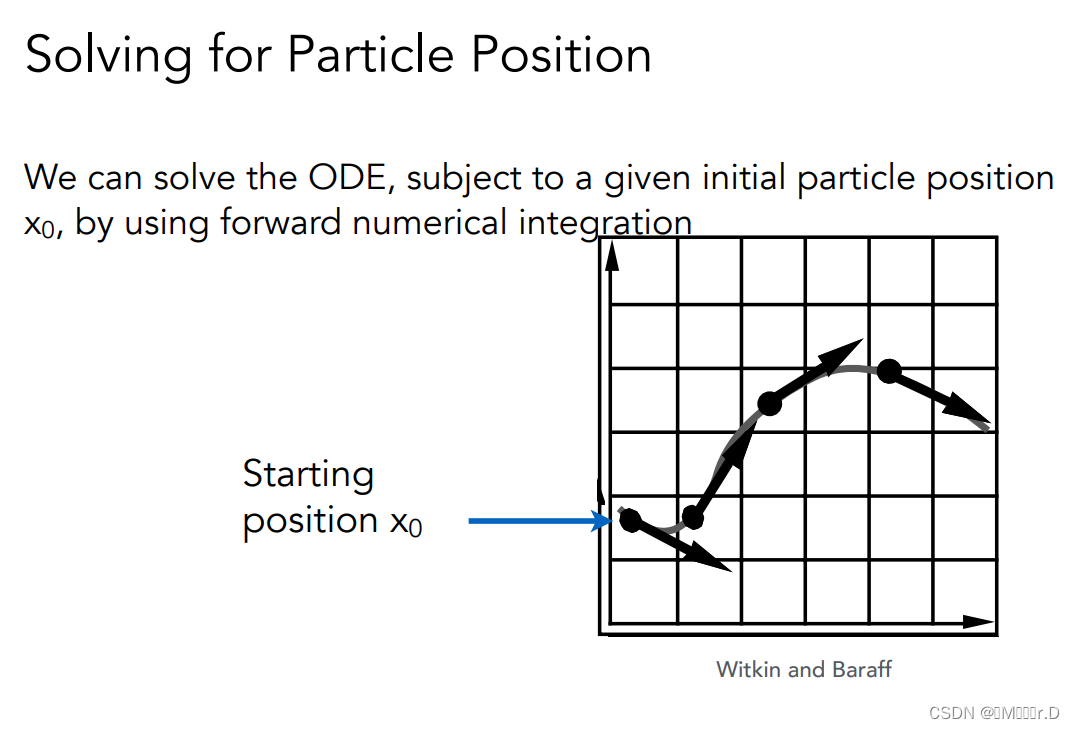
1.欧拉方法

• 欧拉方法：用上一时刻的位置、v、a 更新下一时刻

• 问题：不准，有误差

• 稳定性不行，会迅速变得不稳定，并且出现问题会被无限放大累计，也就是出现正反馈

二、解决“不稳定”

1.Midpoint Method中点法

中点法：在使用欧拉方法时，第一次使用得到中点的速度，然后取中点的速度，重新算一遍欧拉方法

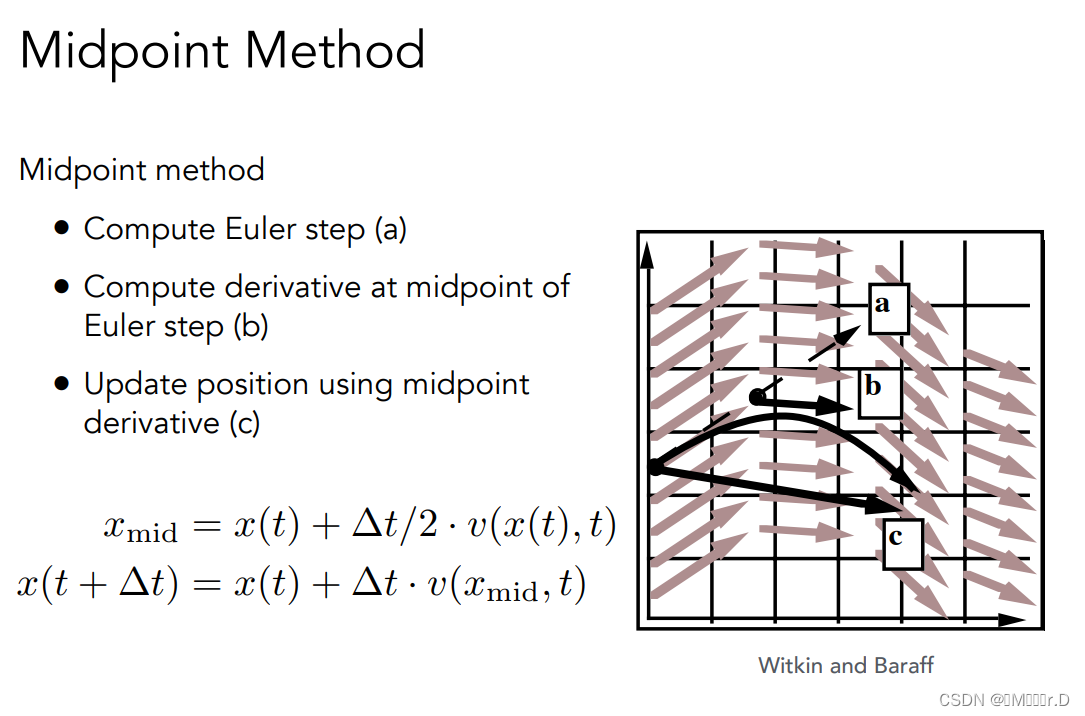
中点法其实是多了一个二次项

2.Adaptive Step Size自适应步长

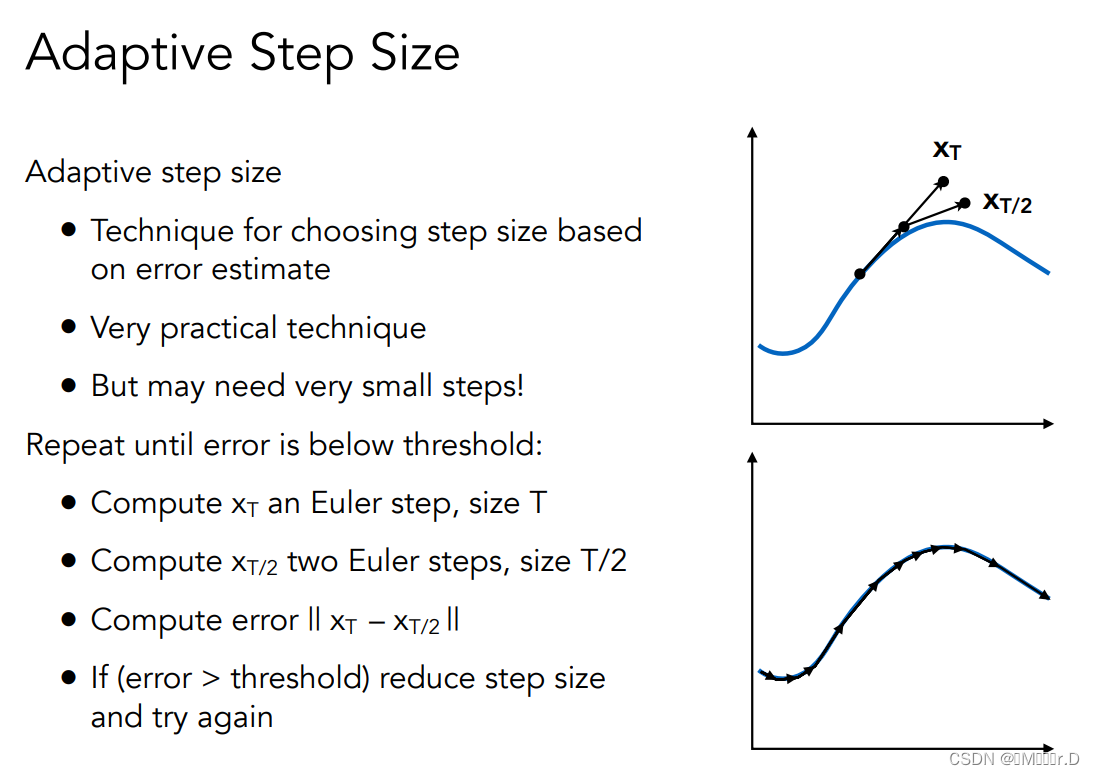
• 结合了中点思想，中点再算一次欧拉

3.Implicit Euler Method 隐式/后向欧拉方法

用下一步的速度和加速度
一开始我们还不知道这些未来的数据，我们要解出当下的数据，不太好解
我们认为这个时刻的位置，下个时刻的加速度都知道，解出下个位置的速度和加速度
用优化方法来解，慢很多，但是稳定性好

• 如何定义不稳定？

• 

• • 局部误差 →累积→ 总体误差
  • 研究他们的“阶“（和△t的关系）
  • 结论：隐式欧拉方法是一阶的（理解：如果h减小一半，误差也减小一半；h减小一半，误差减小到1/4）

• Runge-Kutta Families 龙格库塔方法（一类方法）

• • 擅长解ODE（常微分方程），特别是非线性模型

• • 其中一个用的最多的：RK4（四阶的）
    • 更详细的可以在数值分析课程中

    • 

三、Position-Based / Verlet Integration不是基于物理的方法

1.刚体模拟

2.Fluid Simulation流体模拟

• 通过代表水的体积的小球的位置来模拟水的运动

• • 认为水是不可压缩的刚体小球组成
  • 水在任何位置都不可压缩

• 

• 思路

• • 任何一个时刻小球分布的位置的密度变成和水平静时的不一样，都要修正回来（通过小球的运动）

• 更新过程？

• • gradient descent 梯度下降法（机器学习领域的词）

• 欧拉方法（支点法） VS 拉格朗日方法（网格法）

• • 欧拉方法：把空间分为不同的网格，考虑一个网格的变化；（随着时间等）
  • 拉格朗日方法：eg一群鸟→模拟一只鸟

• Material Point Method (MPM) (结合了欧拉和拉格朗日)