一、思想

归并排序的核心思想是分治法，即将大问题分解成小问题来解决，然后再将解决后的小问题的结果合并以解决原来的大问题。具体包括以下几个步骤：

1. 分解（Divide）：将原始数组不断地二分成更小的子数组，直到每个子数组只包含一个元素，即认为它们已经有序。
2. 解决（Conquer）：递归地对这些子数组应用归并排序，一旦子数组被拆分到只含有一个元素，就开始对其进行两两合并。
3. 合并（Combine）：将两个已经排序的子数组合并成一个有序的数组。这一过程通常涉及比较两个子数组的最前端元素，选择较小的一个放入新的合并后的数组，并移动指针到下一个位置，重复此过程直至所有元素被合并。

归并排序是一种稳定的排序算法，适用于大数据量时效率较高，且可以用于链表等数据结构的排序。然而，它的不足之处在于需要额外的存储空间来存放临时数组，并且对于小规模数据的排序效率不如某些简单的排序算法，如插入排序。此外，由于其递归的特性，归并排序在深度很大的情况下可能会导致调用栈溢出。

二、图解

图解

对于一个这样的数组，首先我们需要将这个数组不断的划分为两个子数组

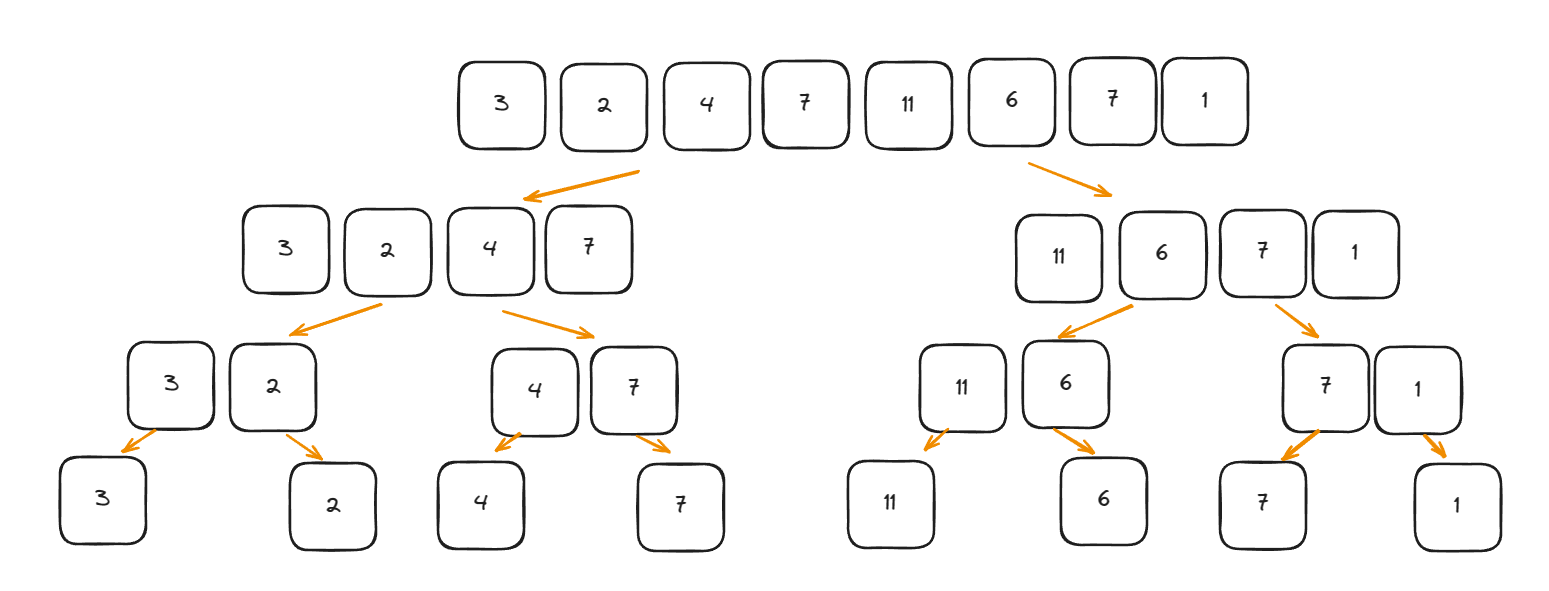
分解代码如下

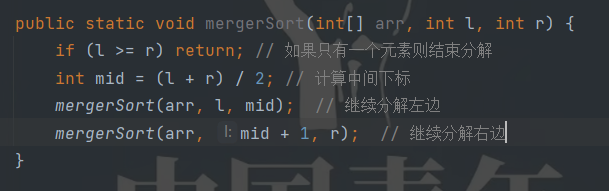
然后将这些子数组逐个排序合并

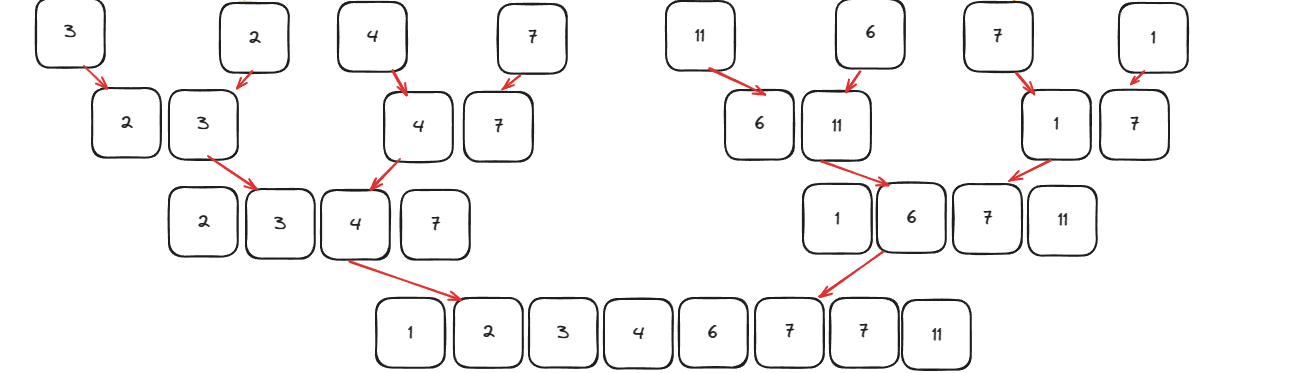
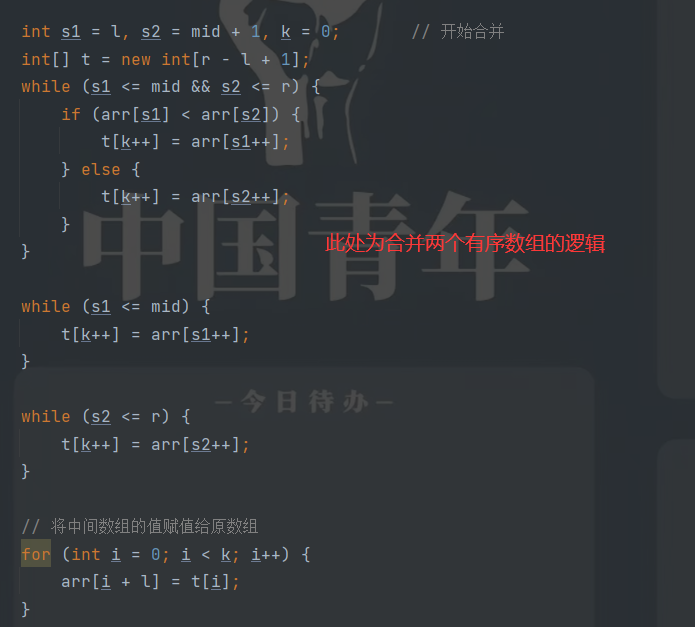
合并代码如下：

整体图示如下：

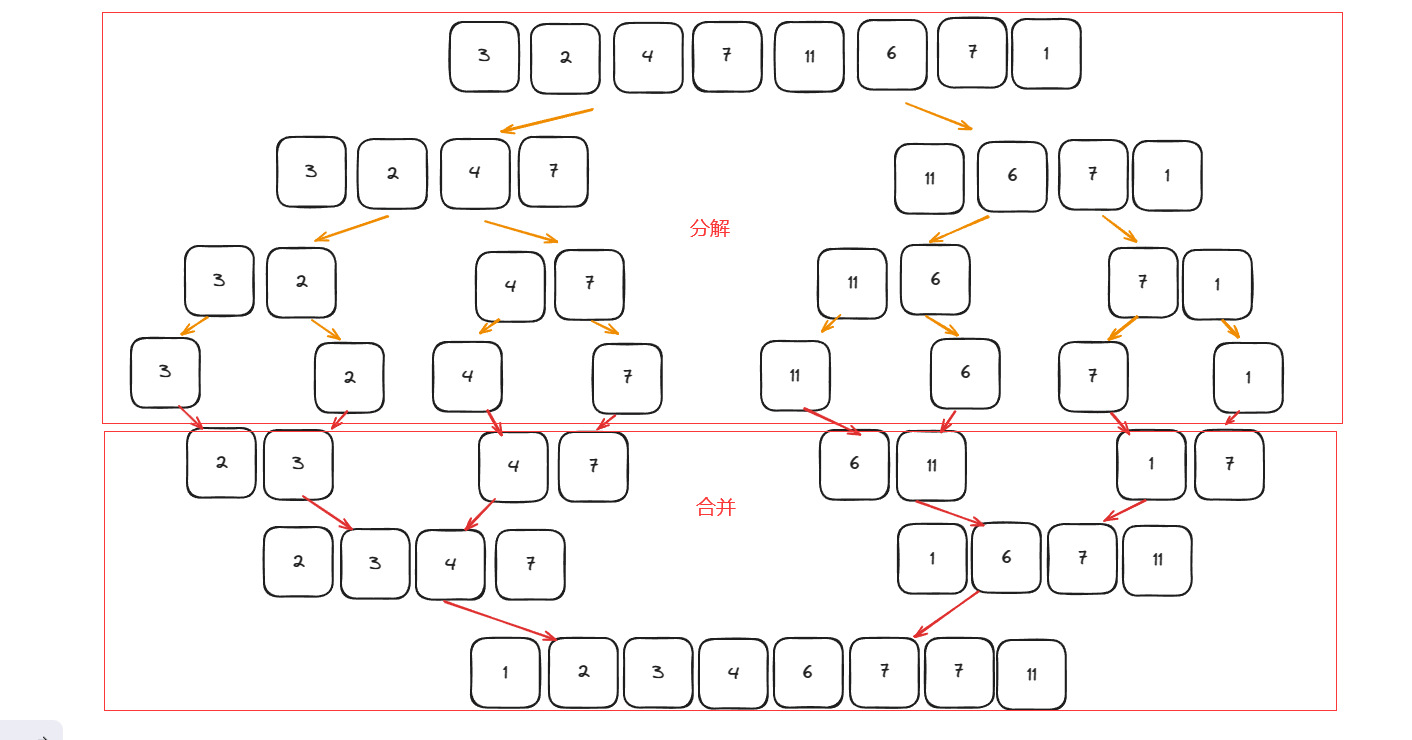
三、代码实现

void merger_sort(vector<int>& arr, int l, int r) {
    if (l >= r) return;
    int mid = (l + r) / 2;
    merger_sort(arr, l, mid);
    merger_sort(arr, mid + 1, r);

    int k = 0, s1 = l, s2 = mid + 1;
    vector<int> t(r - l + 1);
    while (s1 <= mid && s2 <= r) {
        if (arr[s1] < arr[s2]) t[k++] = arr[s1++];
        else t[k++] = arr[s2++];
    }

    while (s1 <= mid) t[k++] = arr[s1++];
    while (s2 <= r) t[k++] = arr[s2++];

    for (int i = 0; i < k; i++) arr[i + l] = t[i];
}

public static void mergerSort(int[] arr, int l, int r) {
        if (l >= r) return; // 如果只有一个元素则结束分解
        int mid = (l + r) / 2; // 计算中间下标
        mergerSort(arr, l, mid);  // 继续分解左边
        mergerSort(arr, mid + 1, r);  // 继续分解右边

        int s1 = l, s2 = mid + 1, k = 0;       // 开始合并
        int[] t = new int[r - l + 1];
        while (s1 <= mid && s2 <= r) {
            if (arr[s1] < arr[s2]) {
                t[k++] = arr[s1++];
            } else {
                t[k++] = arr[s2++];
            }
        }

        while (s1 <= mid) {
            t[k++] = arr[s1++];
        }

        while (s2 <= r) {
            t[k++] = arr[s2++];
        }

        // 将中间数组的值赋值给原数组
        for (int i = 0; i < k; i++) {
            arr[i + l] = t[i];
        }
    }