paper：https://arxiv.org/abs/2310.05055
code： https://github.com/Raman1121/FairTune

摘要和介绍

人工智能在医疗健康应用中的应用正在迅速增长。然而，人工智能模型一再被证明对不同的人口统计学亚群体表现出不必要的偏见——AI模型在由性别、种族、年龄和社会经济地位等方面处于弱势群体中提供了明显更差的表现。该论文认为深度学习模型在训练集中已经在本质上是公平的，在训练阶段不同群体是公平的（表现出相同的性能），但是因为模型在不同群体的泛化能力不同，导致在测试集和现实中存在不公平（表现出不同的性能），如下图所示。

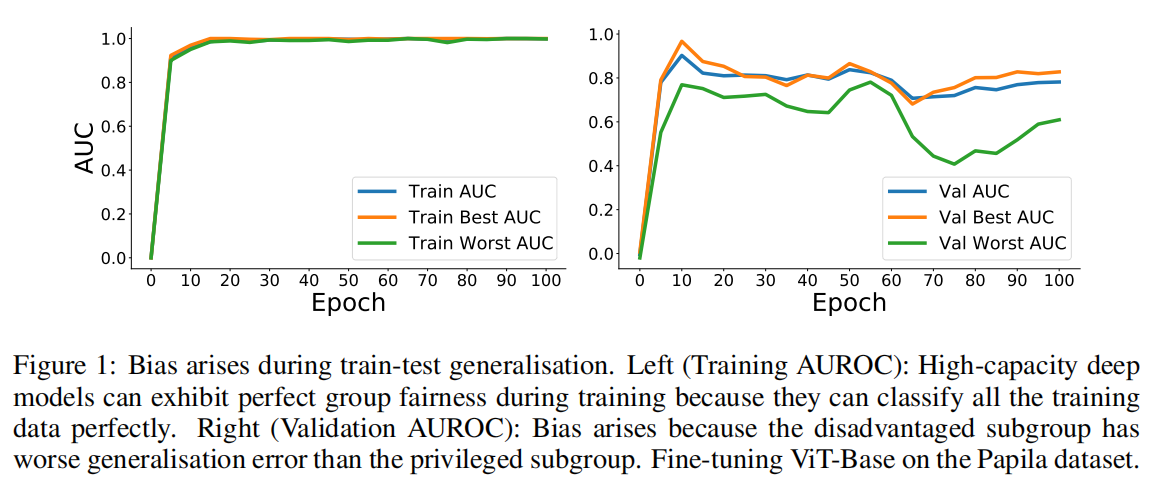
本文的方法植根于容量控制（capacity control）的概念，包括在学习过程中引入一种正则化方法，以最小化看不见的数据的偏差。为了实现这个方法，本文选择了预训练/微调框架。首先在image数据集上进行预训练，然后在小规模医疗图像数据集上微调，在微调阶段，随着更新次数的增加，就出现了上图的情况。因此，主要的挑战在于限制模型更新的程度。本文证明了使用参数高效的微调技术，其中包括对网络参数子集的选择性更新，可以导致更公平的泛化。然而，这种方法有一个关键问题：“应该更新哪些参数以实现公平最大化？”为了解决这个问题，本文引入了名为FairTune的框架，旨在搜索最优参数更新mask。本文寻找的mask是，当应用于约束微调过程时，会对验证数据产生高度的公平性。本文的实验结果表明，在各种医学图像基准中，FairTune在公平性方面优于经验风险最小化（ERM）。
本文主要贡献如下： (1)本文直接证实了Zietlow等人（2022年）的猜想，即在泛化过程中会出现偏见（如上图所示）。(2)与现有的公平干预方法相比，本文引入了一种新的公平学习方法，规范学习，以优化测试阶段的公平性（cf：现有的针对训练集公平性的方法）。(3)本文在不同的基准测试中进行的实证发现一致表明，FairTune比ERM可靠地提高了性能。

相关工作

相关工作介绍了三个部分的内容（1）医学模型的公平性是一个复杂的问题。（2）目前公平性干预的方法主要集中于训练集。（3）所有现有的PEFT方法都存在一个核心挑战，即，它们依赖于启发式方法将参数划分为冻结/更新分区。目前的方法并没有提供一个有原则的或有经验的方法来建立最优分区。这变得特别重要，因为理想的PEFT假设，即冻结/更新分区，可能依赖于数据集。例如，与较小的数据集相比，更大的数据集可以容纳更广泛的参数更新，而不会出现过拟合。

方法

公平性度量

给定一个图像x，我们以一种独立于任何敏感属性s（年龄、性别、种族等）的方式来预测其诊断标签y。这样，训练的模型是公平的，不会使任何不利的特定的人口亚组。大多数实验中，本文优化最弱势群体表现的指标。在这种情况下，给出了数据集D上的模型θ的损失函数$\mathcal{L}(\mathcal{D},\theta )$。假设它可以被数据集D的不同子组s计算为$\mathcal{L}({\mathcal{D}}_s,\theta )$。那么，公平学习的度量标准是${\mathcal{L}}^{fair}={\max }_{s\in S}\mathcal{L}({\mathcal{D}}_s,\theta )$。还是用其他指标比如公平性差距${\max }_{s\in S}\mathcal{L}({\mathcal{D}}_s,\theta )-{\min }_{s\in S}\mathcal{L}({\mathcal{D}}_s,\theta )$。

PARAMETER-EFFICIENT FINE-TUNING

PEFT中，只需要微调参数的一部分$\varphi \subset \theta$。PEFT策略可以解释为指定一个稀疏二进制掩码$\omega$，它决定应该更新$\theta$的哪些部分。给定预训练模型的参数${\theta }_0$和将应用于其值的变化${△}_{\varphi }$，微调过程可以描述为:
${△}_{\varphi }^{\ast }=\arg {\min }_{{△}_{\varphi }}{\mathcal{L}}^{base}({\mathcal{D}}^{train};{\theta }_0+\omega \odot {△}_{\varphi })$
其中${\mathcal{L}}^{base}$为损失函数。
不同的PEFT方法本质上对应于二进制掩模$\omega$的稀疏性结构上的不同结构。
然而，有两个关键的突出挑战： (1)最优的PEFT策略（二进制掩码ω）是依赖于数据集的。例如，更稀疏的掩模ω可能适合较小的目标任务，而更密集的掩模可能适合与训练前任务更不同的任务，因此需要更强的适应。(2)最优的PEFT策略可能取决于最终的泛化目标。例如，与传统的总体泛化相比，稀疏掩模ω可能更适合公平泛化。本文提出了一个解决方案，通过引入一个算法来优化掩模ω关于一个公平的泛化目标。

OPTIMISING PEFT FOR FAIRNESS

从一个预先训练的模型${\theta }_0$开始，和一个数据集$D$，它分为训练、验证和测试集$D_{train}，D_{val}，D_{test}$。每个数据集$D=（X，Y，S）$包含一组图像$X$、标签$Y$和敏感属性元数据$S$。还为PEFT掩码$\omega \in \Omega$定义了一个搜索空间。目标是在进行PEFT学习时找到能导致最佳的公平泛化能力。
**Bi-level Optimization (双层优化，BLO)：**本文将问题陈述形式化为一个由一个内环和一个外环组成的双层优化问题。在内环中，使用传统的损失函数$L^{base}$和PEFT掩模$\omega$对医疗数据集（Dtrain）上的预先训练好的模型进行微调。在外环中，搜索PEFT掩模$\omega$，它导致内环在验证集（Dval）上产生最公平的结果，由$L^{fair}$测量。可以通过以下公式进行表示：
$$\begin{gathered} {\omega }^{\ast }=\arg {\min }_{\omega }{\mathcal{L}}^{fair}(\mathcal{D};{△}_{\varphi }^{\ast }) \\ {△}_{\varphi }^{\ast }=\arg {\min }_{△\varphi }{\mathcal{L}}^{base}({\mathcal{D}}^{train};{\theta }_0+\omega \odot {△}_{\varphi }) \end{gathered}$$
过程可以用下图表示。在实验中，本文采用了一种混合方法，采用无梯度树结构的Parzen估计器（TPE）并采用连续减半（SH）策略来优化外环的${\omega }^{\ast }$，在外环使用梯度下降算法微调${△}_{\varphi }^{\ast }$。

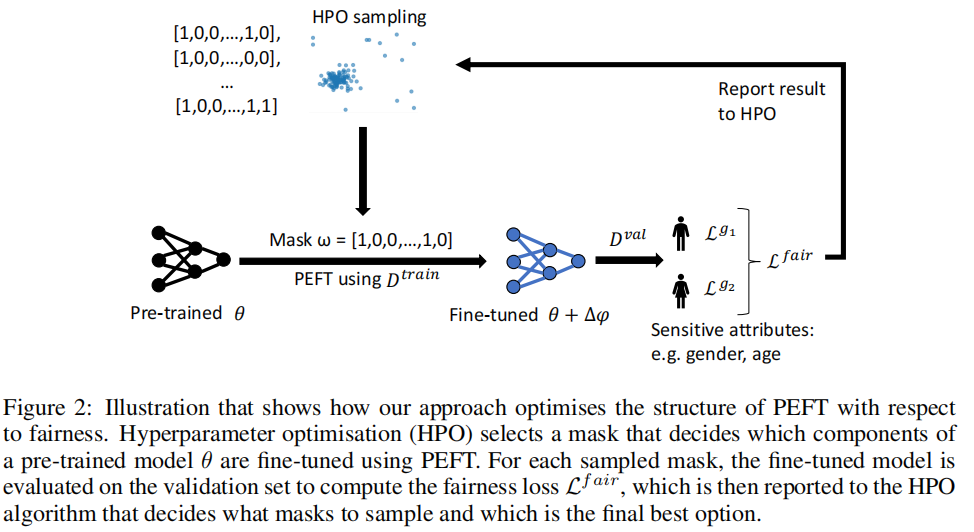
除了选择性更新掩模ω外，学习率α还提供了一个关于更新量的粗略提示。例如，适当地降低学习速率可以防止图1中所示的最异常的过拟合，算法过程如下所示。

实验结果

如下图所示

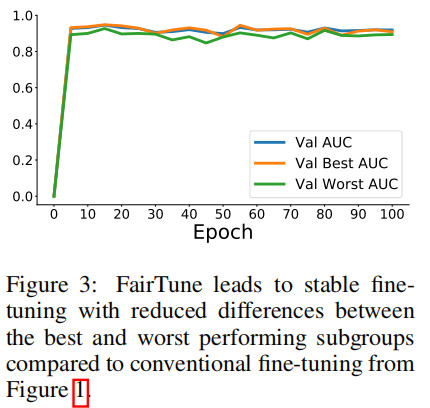
Limitations

下游公平性性能的提高是以计算为代价的，因为它需要我们尝试二进制掩码的各种配置，每个配置对应于一个模型再训练。