基于带时间窗口的电动汽车路由问题的精英对立学习的多群PSO（2022）

英文：Multi-swarm PSO based on Elite Opposite Learning on Electric Vehicle Routing Problem with Time Window

摘要：

带时间窗口的电动汽车路由问题（EVRPTW）是交通领域的一个新问题，用传统的精确求解方法很难解决。启发式算法通常用于解决EVRPTW并获得近似的最优解。我们使用混合整数线性编程对EVRPTW进行建模，同时考虑到实践中遇到的各种因素。作为一种启发式的求解算法，基于精英反向学习的多群粒子群优化算法（M-PSO-EL）对于解决EVRPTW的高维复杂问题具有更快的接收速度和可搜索性。基于EVRPTW设计电动汽车的充电策略。遗传算法（GA）、离散量子行为粒子群优化（DQPSO）和M-PSO-EL在包含不同类型客户点分布的Solomon基准上进行了测试。实验结果表明，M-PSO-EL可以有效地解决有100个客户点的EVRPTW。

引言

以碳排放为重点，通过增加车辆是电池电动汽车（BEV）的约束条件，提出了电动汽车路由问题（EVRP）[1]。与内燃机汽车相比，BEVs的噪音产生最小，由可再生能源驱动[2]。由于电池容量的限制，当BEVs完全充电时，交付里程比内燃机汽车少480-650公里[3, 4]。因此，需要考虑电动车的充电问题。考虑到客户点的有效服务时间窗口的限制，提出了一个带时间窗口的电动汽车路由问题（EVRPTW）[5]。

EVRPTW求解方法已经成为一个研究热点和未来发展趋势。许多学者已经取得了一些成就。Keskin[6]放宽了全电荷限制并允许部分电荷（EVRPTW-PR），开发了一种自适应大邻域搜索。结果表明，这种方法可以有效地找到高质量的解决方案，而且一些充电方案可以显著改善路由。Kucukolu[7]提出了一种用于EVRPTW的模拟退火算法，该算法结合了基于分支和基于边界的站点插入，将充电站插入到可行的路径中。Booth[8]提出了第一个用于建模和解决EVRPTW的约束性编程方法。不同目标的结果表明，对于所有的问题类别，单一资源转换比替代资源模型更好，对于大多数大问题和中问题类别，单一资源转换比MILP更好。

在本文中，EVRPTW被认为是混合整数线性规划（MILP）模型[9]。优化目标函数的组成考虑到了交付成本、完成时间和客户满意度。EVRPTW需要在分配过程中关注车辆的剩余功率和可用里程数[10]。我们设计了一种基于精英反向学习的多群粒子群优化算法来解决多目标EVRPTW。经典遗传算法（GA）[11-13]和离散量子行为粒子群优化（DQPSO）算法[14]在Solomon标准测试集上进行了实验比较。

2 问题公式化

EVRPTW模型是基于CVRPTW的，使用纯电动汽车作为配送车辆[15]。EVRPTW模型能够由图൐ܣǡܸൌ൏ܩ描述，其中顶点׫ܨ׫ܥൌܸܦ଴的集合包含：ܥ的ܰ௖客户，ܨ的ܰ௙充电站加上（ܰ௙ǯ）它们的克隆，以允许多次访问充电站作为基本路线，ܦ଴代表仓库集合，作为每条路线的起点和终点。此外，子集ǯܸ表示ܦ̳ሼܸ ଴ ሽ 。弧的集合A包含所有有序的顶点对，除了仓库之间的顶点，以及每个充电站的顶点。EVRPTW模型中的数学符号和描述见表1。

此外，ݔ ௜௝௞ , ݓ ௜௞ , ݈ ௜௞被用作二元决策变量。当ݔ௜௝௞ൌͳ表示车辆݇已经通过了݅和݆两点之间的路径时，当ݔ௜௝௞ൌͲ表示没有濁时，ݓ௜௞ൌͳ表示电动汽车݇已经提前到达݅点，需要等待݅点的有效服务时间开始，当ݓ௜௞ൌͲ时，电动汽车݇不需要在݅点进行等待。当݈௜௞ൌͳ时，表示电动汽车k到达݅点的时间比服务时间晚，需要惩罚，当݈௜௞ൌͲ时，车辆在服务时间内到达݅点。EVRPTW模型的优化目标函数可以表示为。

公式。(6)和公式。(7)确保每个客户由一辆车提供服务，(8)-(9)是仓库和车辆负载约束，公式。(10)是充电站的约束条件，公式。(11)是电动车在路线上时的电池消耗约束，(12)是电动车在CS的充电约束。公式。(13)-(16)是时间窗口约束，(17)-(18)是服务时间和等待时间约束，(19)是仓库的时间参数，(20)是路线消除条件。

设计一个充电判断策略，这是在电动汽车完成其客户交付点后需要的。充电判断策略可以描述为：计算电动汽车的当前位置和到达下一个客户点所需的功率，并从下一个客户点开始搜索充电站列表中最近的充电站位置。计算车辆的剩余电力是否足以满足下一个客户点的交付。如果满足将电力分配给下一个客户点所需的功率，则进行分配。如果不是，从充电站列表中选择最近的充电站并对其进行充电。

3解决方法

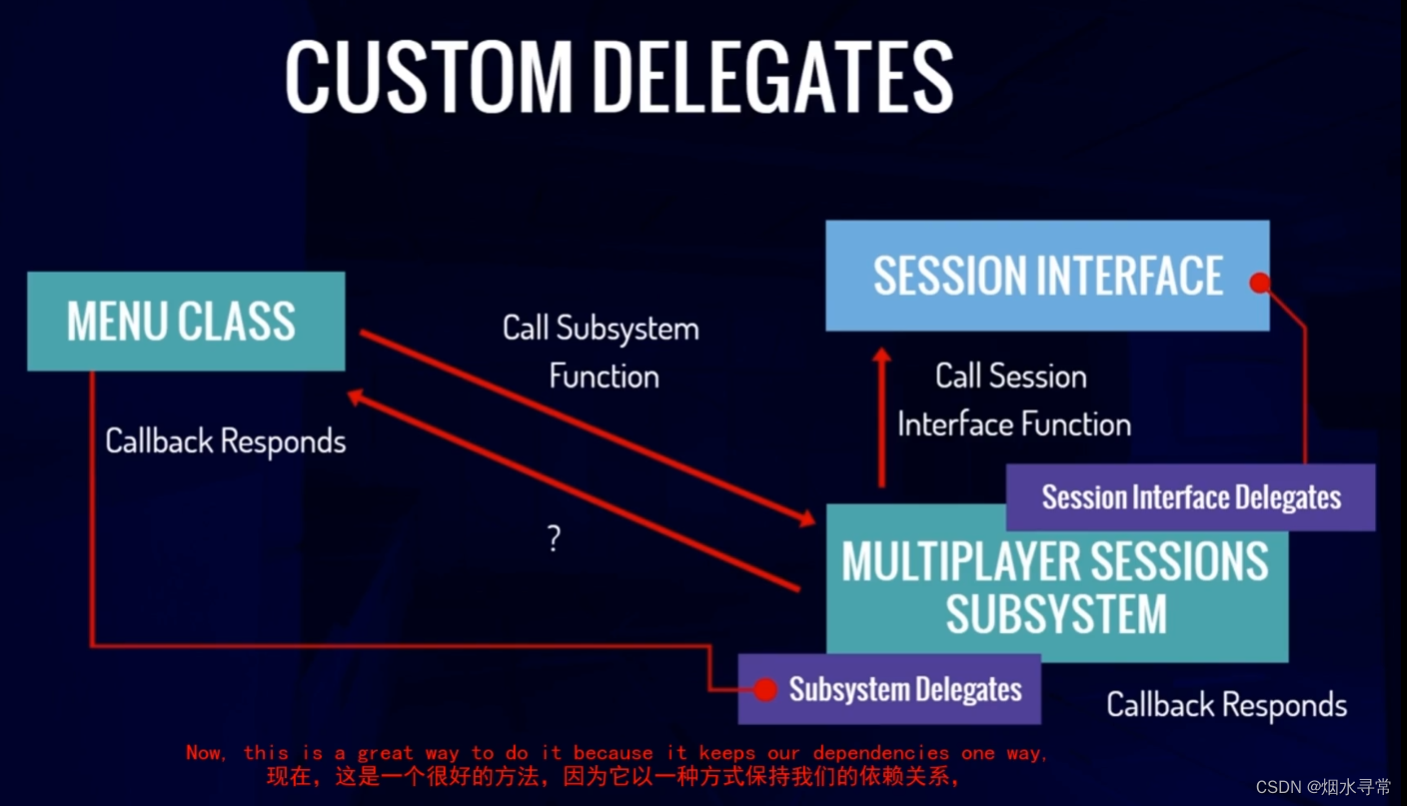
在这篇文章中，我们学习了麻雀搜索算法（SSA）[16]的思想，并设计了基于精英反向学习的蜂群优化算法（M-PSO-EL）来解决多目标EVRPTW。SSA[17]本质上是一种多群粒子群优化算法。M-PSO-EL是基于一个涵盖检测和警告机制的发现者-追随者模型。对于复杂的优化问题，当大多数粒子进入局部最优时，少量的粒子会跳出局部最小值并移动到全局最优方向。通过增加粒子类型和改进粒子迭代公式，在处理高维复杂优化问题时，它具有更快的融合速度和未知区域探索能力。

3.1 初始化策略

对于组合优化问题，种群初始化将大大影响后续的迭代过程。对于函数测试中一小部分非收问题，本文将精英反向学习应用于群体初始化。

M-PSO-EL中的种群初始化如下。随机生成一个种群，并计算种群中每个个体的适应度值。根据适合度值选择精英个体，形成精英群体濁将普通组中的个体转换为反向个体，重新计算并选择适合度值。通过多次迭代形成具有高适应度值的精英组作为初始组。

3.2 位置更新

在M-PSO-EL中，设计了三个搜索粒子，分别是环境搜索粒子、水平搜索粒子和垂直搜索粒子。

环境搜索粒子被用来评估当前搜索空间的搜索质量。环境搜索粒子需要填充整个搜索空间。在搜索其他粒子的过程中提供环境信息。经典的PSO算法与当前速度、当前个体位置和速度更新时的群体位置有关。由于车辆路由问题的高群体相关性，存在搜索范围小的问题。PSO[18]的位置速度更新公式可以表示为

在上式中，c1和ܿc2是学习因子或加速因子，r1和r2是随机数。ܺXb粒子的历史最佳位置，ܺXp是当前群体中的全局最佳位置。

水平搜索粒子侧重于扩大整个群体的搜索范围，只关注它们自己的速度和位置更新。在经典的PSO速度迭代公式中，粒子在前一时刻的位置制约着速度。为了扩大搜索范围粒子的能力，位置限制被从速度更新中移除。

在解决EVRPTW时，水平搜索粒子需要扩大搜索空间。为了解决种群集中的问题，模型的解被困在难以逃脱的局部最优值中。在i时刻݅，只考虑速度信息。水平搜索粒子的速度和位置。

在公式（22）中， $\alpha$ 是一个随机数，݉݁item是最大迭代次数。

垂直搜索粒子专注于搜索的深度并进行垂直搜索。垂直搜索粒子专注于搜索的深度并进行垂直搜索。从位置更新中删除速度。在更新过程中，个人和全局位置信息都被使用。垂直搜索粒子使用公式（23）[16]进行位置更新。

在公式（23）中，Q是一个具有正态分布的随机数，L是一个具有ܰ1*Nc维度的全1矩阵，Xp是当前种群的全局最优位置，ܺ Xworst是全局最差位置。N代表种群中按适配度排序的个体总数。A代表一个݀1*d的矩阵，其中每个元素被随机分配一个1或者-1的值.

环境搜索粒子、水平搜索粒子和垂直搜索粒子构成一个最佳搜索的群体。环境搜索粒子收集并利用个体和种群的速度和位置信息。为了扩大种群的搜索范围，水平搜索粒子不受个体和种群位置信息的限制。只考虑个体在最后时刻的速度和位置信息。垂直搜索粒子收集其他粒子和整个群体的信息，深入搜索以找到最优值。因此，M-PSO-EL可以有效地提高搜索质量。

3.3 求解过程

基于M-PSO-EL的EVRPTW模型求解过程可以表示为。

步骤1：模型参数初始化。

第二步：对实例信息进行编码并初始化群体。

第3步：计算和排序适应度值。

第四步：更新水平搜索粒子、垂直搜索粒子和环境搜索粒子的位置。

第5步：计算适应度值。

第6步：确定是否达到了最大迭代次数，如果不是，则继续执行第3-5步。

第7步：解码并输出结果。

4. 数学实验

4.1 实验设计和参数设置

我们所有的实验都是在台式电脑上进行的，处理器（Intel(R) Core(TM) i7-7700K CPU @ 4.20GHz）和RAM（16.0GB）。所有的算法和测试程序都是用Python编程实现的。实验中使用的测试数据是一个标准的功能测试集。测试实例包括一个仓库、20个充电站和100个客户。EVRPTW数据集的客户点分布根据地理位置分为三类：随机客户分布（R），聚类客户分布（C），以及混合R和C（RC）。

在实验中，EVRPTW调度方案中的固定参数是统一设置的，可以根据实际情况进行调整。相关参数的单位已被归一化，具体数值见表2。

车辆启动成本 1 单位分配成本 0.1 单位等待成本 0.2 单位延迟成本3 客户满意度 3

客户不满意 5 目标函数权重[0.5 0.3 0.2]

电动汽车的车辆参数在EVRPTW标准测试数据集中提供。电动汽车的相关参数显示在表3中。

电动汽车参数参数值

车辆油箱容量 79.69

车辆负荷容量 200.0

燃料消耗率 1.0

逆向加油率3.39

平均速度1.0

我们使用GA、DQPSO和M-PSO-EL来解决EVRPTW模型。GA、DQPSO和M-PSO-EL的算法参数见表4。算法参数由预实验决定，以确保三种算法在实验过程中达到最佳结果。

表4.算法参数算法参数参数值

GA 迭代 500 种群大小 250 交叉概率 0.5 突变概率 0.3

DQPSO 迭代 3000 种群大小 250 扩展-收缩因子 0.8

M -PSO-EL 迭代 3000 种群大小 250 水平搜索粒子比率 0.2 垂直搜索粒子比率 0.5 环境搜索粒子比率 0.3 上边界 500 下边界 0

4.2 实验结果和分析

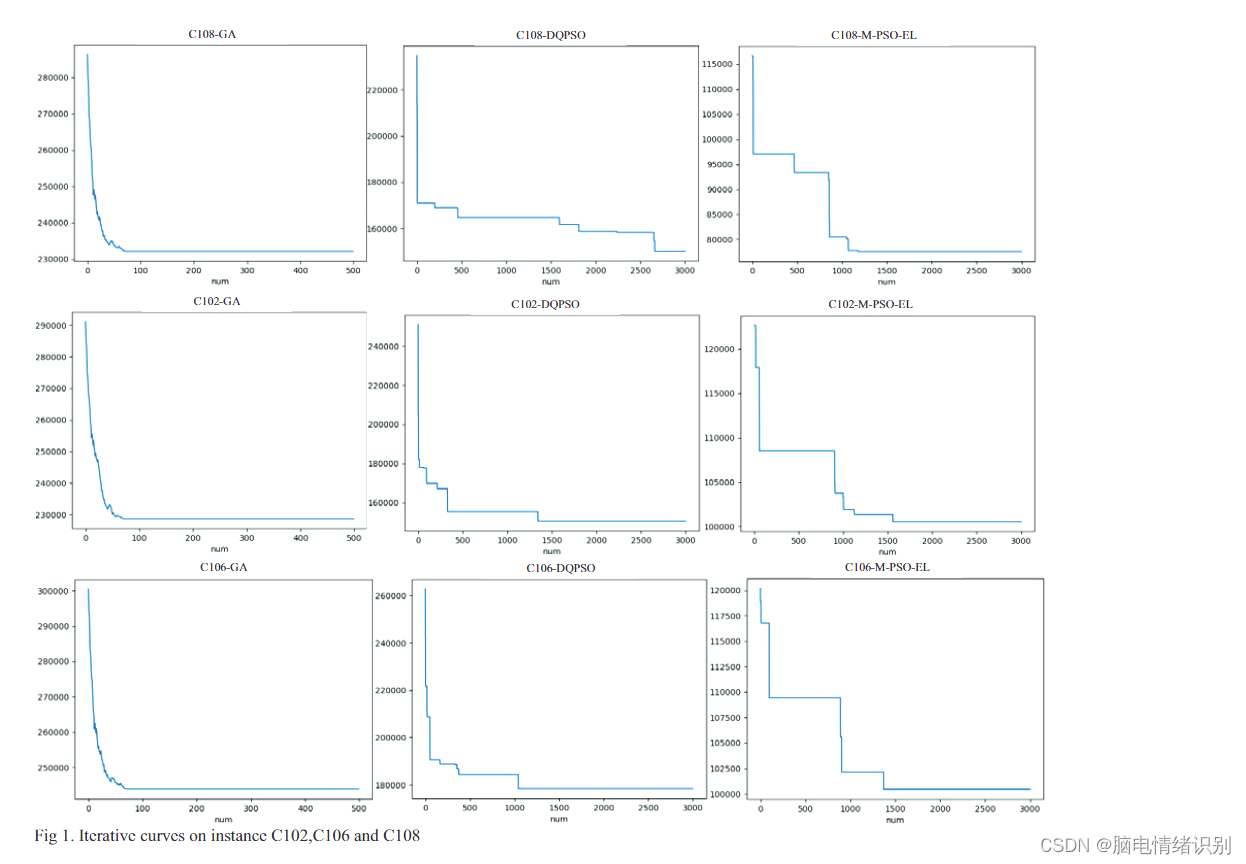
使用GA、DQPSO和M-PSO-EL方法测试了olomon-s基准。记录每个算法的输出并打印迭代曲线。在这篇文章中，在一个有客户点集群的数据集上选择了一个典型的测试案例。

对于每个测试实例，每个算法独立运行20次，设置不同的时间作为算法的终止条件，并根据客户点数量的大小记录算法的运行时间。同时，输出适应度曲线以确定算法在平滑位置的迭代次数并记录下来。在本文中，BestVal、WorstVal和AvgVal被用来表示20种独立运行算法的最佳、最差、平均和平均时间，OptVal是所有算法的最佳值。

实例C102、C106和C108都属于Solomon基准中的集群客户点，仓库和充电站位置一致。在本文中，选择Solomon基准中不同客户点分布的三个代表性实例来绘制DQPSO和M-PSO-EL的迭代曲线。集群客户点分布实例选择C102、C106和C108（图1）；随机分布客户点实例选择R101（图2）；集群和随机分布混合客户点实例选择RC103（图3）。对于图3中的集群客户点分布，三个实例之间的客户端时间窗口存在差异。C102时间窗口分布在总时间线的前面，时间窗口较窄。T C106时间窗口在整个时间线上均匀分布。C108时间窗口分布在总时间线的后面，并且时间窗口很宽。

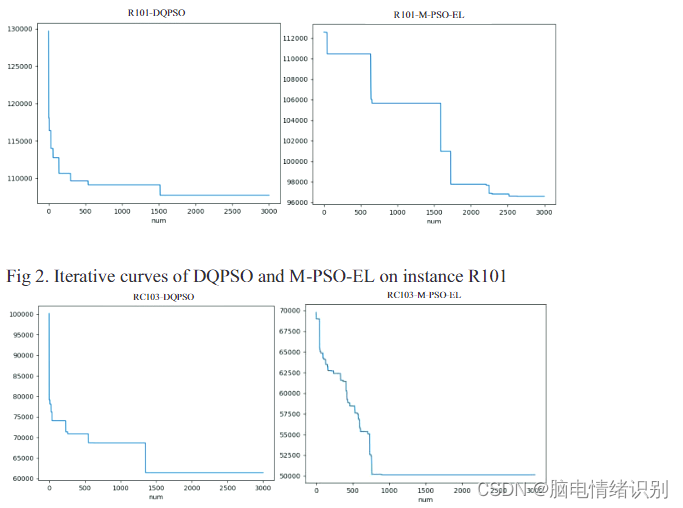
图3.DQPSO和M-PSO-EL在实例RC103上的迭代曲线

在上图中，由于M-PSO-EL增加了一个整体的初始化策略，迭代开始时的总目标函数值明显小于DQPSO。在迭代开始时，DQPSO和M-PSO-EL的目标函数值都以较快的速度下降，然后以较慢的速度下降，逐渐接近找到的近似值。与DQPSO不同，M-PSO-EL可以跳出当前的局部最优，当迭代落入局部最优时，继续根据算法中的警报机制进行搜索。在不同分布类型的客户点实例上，DQPSO在迭代过程中落入局部最优值，直到迭代次数达到设定的最大迭代次数，而且目标函数没有再次下降的趋势或可能性。

而，M-PSO-EL能够落入局部最优，特别是在C101、C106、C108和R101中，对局部最优有显著的限制。由于M-PSO-EL的侦察预警机制和内部竞争的存在，它可以在有限的迭代后跳出局部最优值，转向全局最优值。

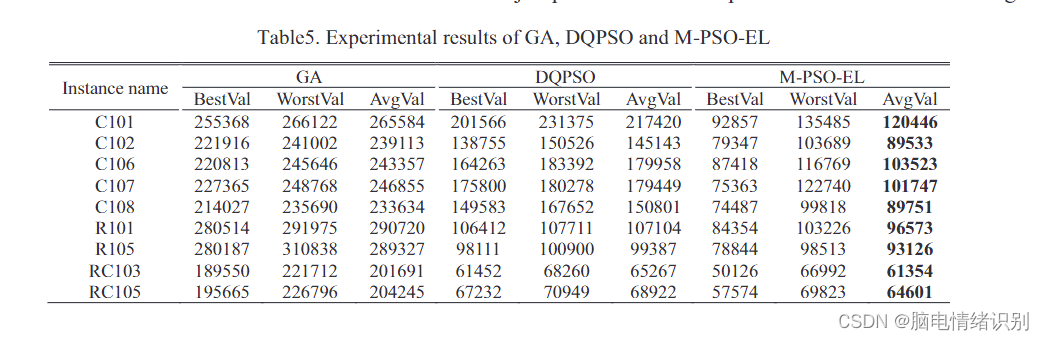
为了更直观地解决不同客户点分布的EVRPTW问题，我们使用了GA、DQPSO和M-PSO-EL三种算法。表5给出了在Solomon基准上求解三种算法的一些实例的结果。共有9个测试用例，其中5个是集群客户点分布测试用例，随机客户点分布和随机集群混合客户点分布是两个。每个实例独立运行20次后，记录݈ܸܽݐ݅ܤ和\1864quot。

基于实验结果，经典启发式算法GA在三种不同类型的客户点测试实例上难以接近全局最优值，容易陷入局部最优值。与DQPSO相比，在测试实例上，M-PSO-EL解的质量高于DQPSO。尽管在求解上花费了时间，但从迭代曲线图中也可以观察到，M-PSO-EL可以通过使用有限次数的迭代来摆脱局部最优解。DQPSO被困在局部最优解中，无法逃脱，导致解的质量低于M-PSO-EL。

5 结论

本文给出了EVRPTW的问题背景描述和线性混合整数编程模型的数学表示。总分配成本、总分配时间和客户满意度被线性加权为总目标函数。本文设计了M-PSO-EL来解决EVRPTW模型，并使用GA和DQPSO作为比较算法。在Solomon-s基准的EVRPTW数据集上的测试实例是聚类的，随机分布的，以及聚类的随机分布的客户点。结果表明，M-PSO-EL在不同类型的客户点分布中具有更好的解决方案质量。M-PSO-EL在求解过程中显示的不稳定性也是摆脱局部最优解的一种表现。