123

二分+等差数列求和+前缀和数组

题目分析

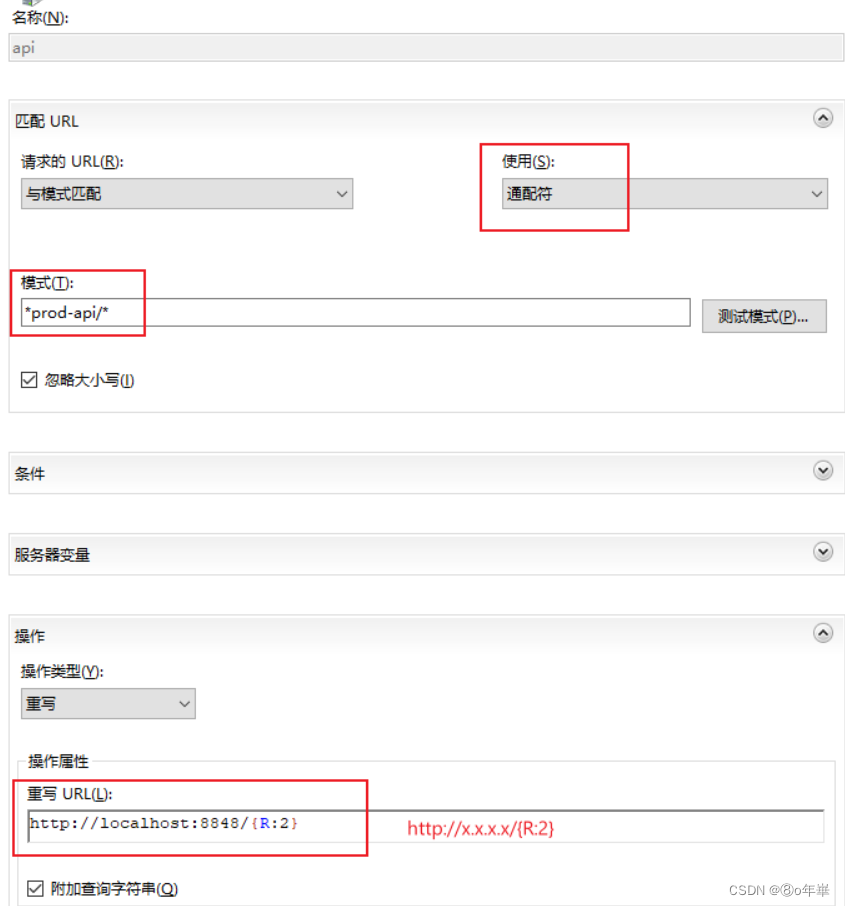
连续一段的和我们想到了前缀和，但是这里的l和r的范围为1e12，明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点，可以按照等差数列对序列进行分块。如上图，在求前10个数的和的时候，我们可以这样求1+3（1+2）+6（1+2+3）+10（1+2+3+4）=20。我们不需要遍历10次就可以求出来。求前缀和代码如下

sum = new long[1500010];
for (int i = 1; i <= 1500000; i++) {
    t += i;
    sum[i] = sum[i-1]+t;
}

这里的t最开始等于1，是第一块的数字和，然后等于3，是第二块数字的和，然后等于6是第三块数字的和，以此类推。sum[i]表示的是分块后前i块包含数字的和。

我们可以求出前n块数字的和，那么我们需要知道第l个数字是在哪一块里面，然后求第l个数字是所在块的第几个数字。因为对于最后一块来说，不是所有的数字都会被包含进来，我们要单独对最后一块求数字和。

第一阶段利用二分求第x个数所在的块

​ 图1

如图1所示，我们可以把这个序列分块，第一块有1个数，第二块有2个数，第三块有3个数，第四块有4个数，每一块拥有数的个数是一个等差数列。现在要找到序列中第x个数所在的块数，假设x=3，那么第x个数在第2块中，如果x=4，那么第x个数在第3块中。求第x个数所在的块数，就是求从左往右数，前缀和第一个大于等于x的块。

比如第2块的前缀和就是3，第三块的前缀和就是5。这个可以用二分去求。

    int l = 1;
    int r = 1500000;//最多可以分的块数
    while(l < r) {
        int mid = (l + r) / 2;
        if(sum(mid) < x) {//求mid个块中包含的数字的个数，如果小于x，就是不符合条件，我要向左找
            l = mid + 1;
        }else {//符合条件，我要看前面的块是否也是大于等于x的
            r = mid;
        }
    }

这里的sum函数的作用就是求前mid块中包含的数字的个数，因为是等差数列，所以直接用等差数列的求和公式就可以了，sum函数如下

private static long sum(long x) {    
    return (1L + x) * x / 2;
}

第二阶段求前x个数的前缀和

接下来分析二分结束之和我要怎么操作，我要求前x个数字的和。

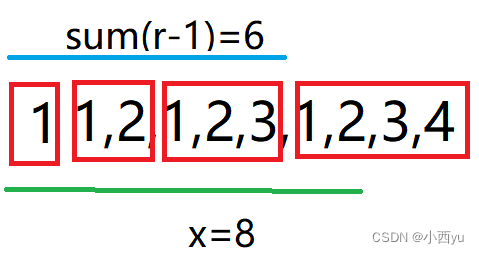
假设x=8，那么第x个数在第4块中，我还要知道，第x个数是第4块中的第几个数字。如图，第4块有4个数，第x个数第4块的第2个数上，那么第2个数是怎么来的呢？就是x-sum(r-1)=8-6=2。其实就是我二分算出来了第x个数在第r块上，那么我只需要把前r-1块包含的数的个数减去就算出来x是在第r块上的第几个数上了。结合上图更好理解。那么前x个数的和就是前r-1块包含数的和加上第r块里面前x-sum(r-1)个数的和。

某一块里面包含的数也是等差数列，求前n个数的和依然可以直接用sum(n)去求。而数组sum[r]里面记录的是前r块包含数字值的前缀和。所以二分结束后的代码是这样子的

private static long f(long x) {
    int l = 1;
    int r = 1500000;//最多可以分的块数
    while(l < r) {
        int mid = (l + r) / 2;
        if(sum(mid) < x) {//求mid个块中包含的数字的个数
            l = mid + 1;
        }else {
            r = mid;
        }
    }
    //r--是表示完整的块的个数
    r--;//就是上文里的r-1
    //x表示x处在他所在块的第几个位置，需要减去前面所有块包含的数的个数
    //本来要求x个数字，前r个块中已经包含了sum(r)个数字，第r+1个块
    x -= sum(r);//前r个块中已经包含了多少个数字
    return sum[r]+sum(x);
}

还是对于x=8的例子，二分求出来r=4，r–后，r=3，sum[3]=10。x-=sum(3)=8-6=2。sum[3]+sum(2)=10+3=13

注意这道题里对于sum函数的多次应用，但是不是每一次应用含义都是一样的。因为每一块包含的数字个数是等差数列，而每一块内每个数字形成的也是等差数列。

题目代码

import java.util.Scanner;
public class Main {
static long[] sum;
public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    long t = 0;
    //前缀和的预处理
    sum = new long[1500010];
    for (int i = 1; i <= 1500000; i++) {
        t += i;
        sum[i] = sum[i-1]+t;
    }
    int n = scanner.nextInt();
    while(n-- > 0) {
        long l = scanner.nextLong();
        long r = scanner.nextLong();
        System.out.println(f(r)-f(l-1));//f(r)求的是序列中前r个数的和
    }
}
//二分  二分求的是x在哪一块中 n*（n-1）/2>l的第一个n
private static long f(long x) {
    int l = 1;
    int r = 1500000;//最多可以分的块数
    while(l < r) {
        int mid = (l + r) / 2;
        if(sum(mid) < x) {//求mid个块中包含的数字的个数
            l = mid + 1;
        }else {
            r = mid;
        }
    }
    //r--是表示完整的块的个数
    r--;
    //x表示x处在他所在块的第几个位置，需要减去前面所有块包含的数的个数
    //本来要求x个数字，前r个块中已经包含了sum(r)个数字，第r+1个块
    x -= sum(r);//前r个块中已经包含了多少个数字
    return sum[r]+sum(x);
}
//sum函数求前x块包含的数的个数，同时也可以表示某一个块中，前x个数的总和
private static long sum(long x) {
    // TODO Auto-generated method stub    
    return (1L + x) * x / 2;
}
}