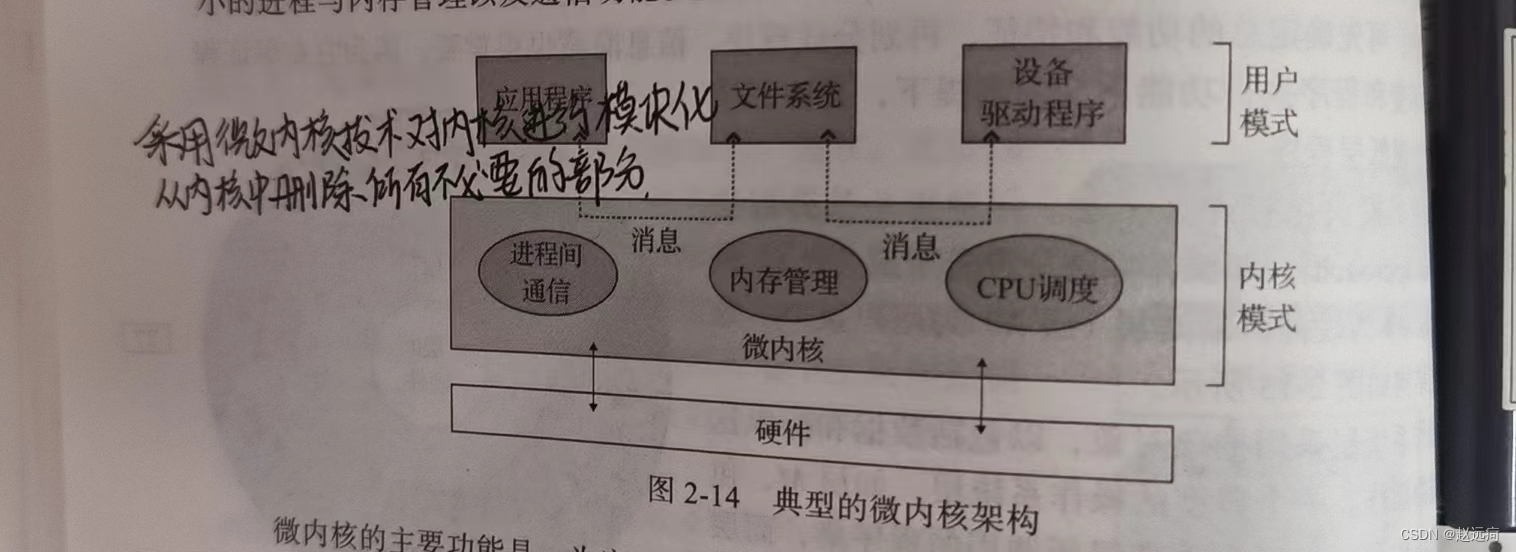
今日复习内容：做题

例题1：体育健将

问题描述：

小蓝作为班级里的体育健将，他被安排在校运会时参加n个体育项目，第i个体育项目参赛需要耗时ai分钟，赛后休息需要bi分钟（这意味着当他参加完这场比赛后需要经过bi分钟才能再次参加其他项目）。

由于小蓝实在太强了，无论 参加任何比赛他都可以拿到金牌，但他能够参加校运会的时间有限，最多只能参加k分钟，请问他最多能拿几块金牌？

输入格式：

第一行包含两个整数n和k，表示体育项目数量和小蓝的可参加校运会时间；

第二行包含n个整数a1,a2,...,an，表示每个项目需要的参赛时间；

第三行包含n个整数b1,b2,...,b3，表示每个项目后面需要的休息时间；

数据范围保证：1 <= n <= 2 * 10^5，1 <= ai,bi,k <= 10^8

输出格式：

输出一个整数，表示在k分钟内小蓝最多可以拿到几个金牌

参考答案：

from itertools import accumulate
import bisect
n,k = map(int,input().split())
li1 = list(map(int,input().split()))
li2 = list(map(int,input().split()))
li = [[li1[i] + li2[i],li1[i],li2[i]] for i in range(n)]
li.sort(key = lambda x:x[0])
pre = [li[0][0]]
for i in range(1,n):
    pre.append(pre[-1] + li[i][0])
ans = 0
for i in range(n):
    if k < li[i][1]:
        continue
    tmp = k - li[i][1]
    num = bisect.bisect_right(pre,tmp)
    if num <= i:
        ans = max(ans,num + 1)
    elif num >= n:
        ans = max(ans,n)
    else:
        ans = max(ans,bisect.bisect_right(pre,k + li[i][2]))
print(ans)

运行结果：

 

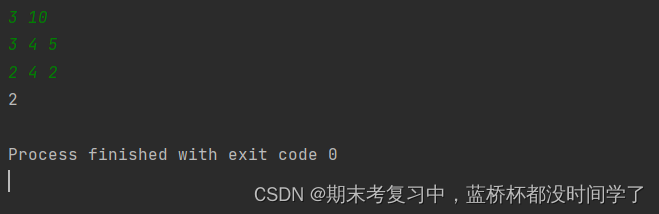
以下是我对此题的理解：

1.输入处理

首先，从输入中读取两个整数n和k，分别表示体育项目的数量和小蓝能参加的时间；

然后，读取了两行整数，分别表示每个项目的参赛时间和休息时间。

2.数据处理

接下来，将每个项目的参赛时间和休息时间相加得到总时间，并将其按照其总时间从小到大排序，同时记录下每个项目的参赛时间和休息时间。

使用accumulate函数计算出累加的总时间，这个总时间列表保存在pre中。

3.计算最多金牌数量

初始化变量ans为0，表示最多金牌数量；

然后对每个项目进行遍历，如果当前项目的参赛时间已经超过了小蓝能够参赛的总时间k，就跳过该项目；

如果参加档期那项目的时间小于等于小蓝能够参赛的时间k，计算剩余时间tmp；

使用bisect_right函数在累加的总时间列表pre中找到剩余时间tmp可以容纳的项目数量num；

如果num小于等于当前的索引i，说明剩余时间只能容纳当前项目及之前的项目，此时最多可以获得的金牌数量为num + 1；

如果num大于等于当前项目的数量n，说明剩余时间可以容纳所有项目，此时最多可以获得的金牌数量为n；

否则，剩余时间可以容纳当前项目及之后的某些项目，通过bisect_right函数找到在剩余时间内可以容纳的项目数量，并更新最多金牌数量ans。

4.输出结果

输出最多金牌数量ans

这道题是通过排序和累加来优化计算过程

然后，我稍微改了一下，也可以这样：

from itertools import accumulate
import bisect

# 读取输入，n表示体育项目数量，k表示小蓝可参加校运会时间
n, k = map(int, input().split())

# 读取每个体育项目的参赛时间和休息时间
li1 = list(map(int, input().split()))  # 参赛时间列表
li2 = list(map(int, input().split()))  # 休息时间列表

# 将每个项目的总时间（参赛时间+休息时间）、参赛时间、休息时间组成一个元组，并按总时间从小到大排序
li = [[li1[i] + li2[i], li1[i], li2[i]] for i in range(n)]
li.sort(key=lambda x: x[0])

# 计算累加的总时间列表
pre = list(accumulate([x[0] for x in li]))

# 初始化最多金牌数量为0
ans = 0

# 遍历每个项目
for i in range(n):
  # 如果参加当前项目的时间已经超过了小蓝能参加的总时间k，则跳过该项目
  if k < li[i][1]:
    continue
  
  # 计算剩余时间
  tmp = k - li[i][1]
  
  # 使用二分查找在累加的总时间列表pre中找到剩余时间tmp可以容纳的项目数量num
  num = bisect.bisect_right(pre, tmp)
  
  # 如果num小于等于当前项目的索引i，说明剩余时间只能容纳当前项目及之前的项目，此时最多可以获得的金牌数量为num + 1
  if num <= i:
    ans = max(ans, num + 1)
  # 如果num大于等于项目的数量n，说明剩余时间可以容纳所有项目，此时最多可以获得的金牌数量为n
  elif num >= n:
    ans = max(ans, n)
  # 否则，剩余时间可以容纳当前项目及之后的某些项目
  else:
    # 通过二分查找在剩余时间内可以容纳的项目数量，并更新最多金牌数量ans
    ans = max(ans, bisect.bisect_right(pre, k + li[i][2]))

# 输出最多金牌数量
print(ans)

---

例题2：小浩的ABC

问题描述：

小浩有一个整数X，他想找到一个三元组（A,B,C）满足：

1 <= A,B,C <= 10^6;      A * B + C = X

在满足条件的情况下，让（B,C,A）的字典序最小，如果不存在这样的三元组则输出-1。

输入格式：

第一行输入一个整数T,表示测试数据的组数；

接下来T行每行输入一个整数X，含义如题所示。

输出格式：

对于每组测试数据，输出A,B,C的值，如果不存在这样的三元组则输出-1，并换行。

参考答案：

def printf(x):
  if x == 1:
    print(-1)
  elif x <= 1e6 + 1:
    print(x - 1, 1, 1)
  else:
    if x % 1e6 == 0:
      print(int(1e6), int(x // 1e6), int(1))
    else:
      print(int(1e6), int(x // 1e6), int(x % 1e6))
T = int(input())
for i in range(T):
  x = int(input())
  printf(x)

运行结果：

 

以下是我对这道题的理解：

先定义一个函数，比如printf，该函数接受一个整数x作为输入；

首先检查x的取值：

如果x等于1，则输出-1，因为无法找到满足条件的三元组；

如果x <= 1e6,则输出A 取x - 1，B和C取1的三元组，因为此时(1,1,x - 1)满足条件，并且字典序最小。

如果x > 1e6 + 1，则需要进一步判断；

如果x能被1e6整除，则将A设为1e6，B设为x除以1e6的商，C为1；

否则，将A设为1e6，B设为x除以1e6的商，C设为x除以1e6的余数。

---

例题3：小新的质数序列挑战

问题描述：

小新是一个热爱数学的孩子，他特别喜欢研究质数。最近，他发现了一个有趣的问题，他想用两个整数A和B来构造两个质数序列。

让我们设P表示一个长度为N的质数序列，使得序列中所有数的和为A；

设Q表示一个长度为M的质数序列，使得序列中所有数的和为B。

设X 表示所有有效对(Pi,Qi)(满足条件1 <= i <= N,1 <= i <= M)的最大绝对差。

现在，小新的挑战就是找出所有可能的P和Q序列中，X的最小可能值。

更正式地说，对于所有可能的序列P和Q，找出max(|Pi - Qi|)的最小值，其中1 <= i <= N,1 <= i <= M。

如果无法形成一个序列，请输出-1。

注意，|X|表示数字X的绝对值。例如|-4| = 4，|7| = 7

输入格式：

首先是一个整数T，表示测试用例的数量，接下来是T个测试用例。

每个测试用例包含两个整数A和B。

数据范围保证：1 <= T <= 10^5，1 <= A,B <= 10^18。

输出格式：

对于每个测试用例，如果无法形成任何一个序列，则输出-1，否则打印max(|Pi - Qi|)的最小值。

参考答案：

import math
t = int(input())
for i in range(t):
    A,B = map(int,input().split())
    if min(A,B) == 1:
        print(-1)
    else:
        if math.gcd(A,B) > 1:
            print(0)
        else:
            print(1)

运行结果：

 

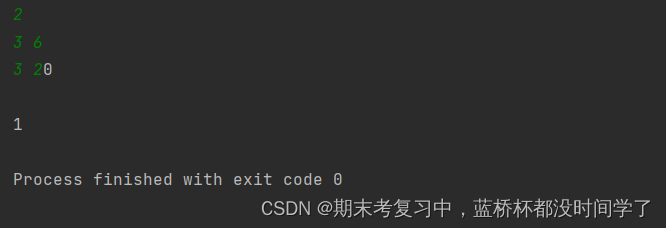
以下是我对此题的理解：

首先读取输入的测试用例数量t；

对于每个测试用例：

读取两个整数A和B，表示要构造的质数序列的和；

如果A和B中有任何一个等于1，那么无法构造出满足条件的质数序列，因为质数序列必须大于1，所以直接输出-1；否则，如果A和B的最大公约数大于1，则说明A和B有共同的质因数，此时无法构造出满足条件的质数序列，因为每个质数只能出现一次，所以最大 绝对差为0，输出0。

如果A和B的最大公约数等于1，说明A和B互质，可以构造出满足条件的质数序列。此时，任意一个质数序列的质数序列的和的最大最大绝对差为1，因为任意两个互质的正整数的差的绝对值至少为1，所以输出1。

主要是利用质数的性质以及最大公约数的概念来判断能否构造出满足条件的质数序列，以及求出最大绝对差的最小值。

---

例题4：小蓝的无限集

问题描述：

小蓝有一个无限集，该集合生成方式如下：

1.集合里面初始元素为1；

2.如果x在集合中，则x * a,x + b均在集合中。

例如a = 2,b = 3时，该集合5个最小元素如下：

1

2。因为2 = 1 * 2

4。因为4 = 1 + 3

5。因为5 = 2 + 3

7。因为7 = 5 + 2

现在有t组数据，每组数据给定你3个正整数a，b，n，由若干个空格分割，含义如题所示。

输入格式：

第一含输入一个整数t，表示测试案例组数。

接下来t行，每行输入3个正整数a，b，n，由若干个空格分开，含义如题所述。

输出格式：

对于每组数据，如果n在集合中，输出Yes，否则输出No。

参考答案：

t = int(input())
for i in range(t):
    a,b,n = map(int,input().split())
    if a == 1:
        if (n - 1) % b == 0:
            print('Yes')
        else:
            print('No')
    else:
        cnt = 1
        flag = False
        while cnt <= n:
            if (n - cnt) % b == 0:
                flag = True
                break
            cnt *= a
        if flag:
            print('Yes')
        else:
            print('No')

运行结果：

 

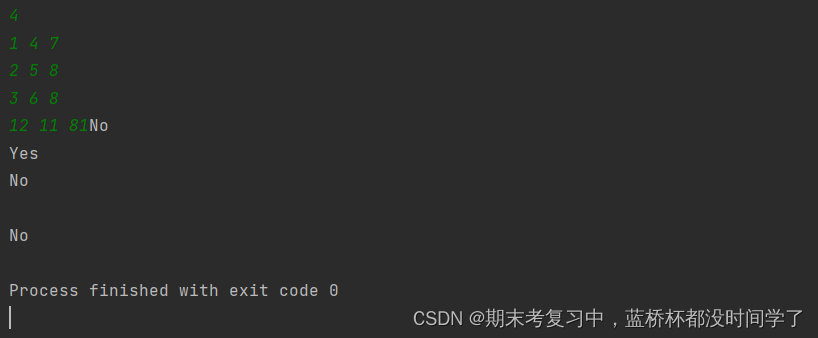
OK，这篇我只写这些题，下一篇继续！