这破题目肝了我一天半才搞明白,也正是因为这道题目,我才豁然明白了李煜所说的"剪不断,理还乱...别是一般滋味在心头"到底是什么"滋味".在完全搞明白之前,真的是放有放不下,理也理不清...

但是理解之后你会发现,嘛い---,也就那么个回事嘛O(∩_∩)O
目录
1.题目:来自力扣
2.为什么选择数组(顺序表)是实现这道题的最好的方案
3. 有如何判断环状顺序表何种情况下为空,以及何种情况下为满的问题
4.需要实现的操作
5.具体操作的代码实现
5.1创建一个顺序表
5.2判空与判满操作
5.3队尾加入新元素操作
5.4队头删除元素操作
5.5显示头操作
5.6重难点:显示尾操作
6.写这条题目时顺便把自己的思路写了一下整理成笔记,分享一下
1.题目:来自力扣

2.为什么选择数组(顺序表)是实现这道题的最好的方案
- 简单性和易实现性:循环队列的实现相对简单,主要涉及数组的索引计算和循环移位。而链表的实现需要处理节点的创建、删除和指针操作,相对复杂
- 时间复杂度:在大多数情况下,循环队列的入队、出队操作的时间复杂度为O(1),因为只需要计算索引和进行简单的赋值操作。而链表的入队、出队操作可能涉及到节点的创建、删除和指针调整,时间复杂度为O(1)或O(n)。
3. 有如何判断环状顺序表何种情况下为空,以及何种情况下为满的问题
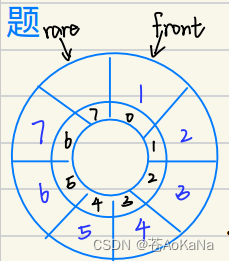
若空:则rear和front⼀定是指向同⼀位置的
若满:因为是循环顺序表(数组)那么理论上rear和front也是 .指向同⼀位置,但是这样便会与判空混淆,是⽆法操作的
这种问题我们称沩「假溢出」
所以,解决此问题的最佳方案便是⽤多额外开辟⼀个空间来解决假溢出问题
为确保队满时rear+1可以指向front,所以每次向队列中添加⼀个元素后rear 要指向当前元素的下⼀个位置,于是便有了rear+=1,然后顺理成章便有了 reart1=front来进⾏判断的代码.
如上图,如果rear到达循环队列最后⼀个位置时, rear=7,rear+1=8,但front =0,这并不符合我们的预期,故⽽我们设了⼀个值K,⽤于表示此循环队列中点共有多少个元素(这其中 包括为了解决假溢出⽽额开辟的空间)
⽤(rare+1)%(k+1)来控制rare范围
ps: k是怎么来的?先⽤malloc开辟整数倍的数组每个元素⼤⼩的空间 此时为k,再realloc对其进⾏扩展⾄(k+1),多⼀个假溢出空间。
4.需要实现的操作
bool myCircularQueueIsFull(MyCircularQueue* obj);//判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj);//判满
MyCircularQueue* myCircularQueueCreate(int k); //初始化
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value);//入队
bool myCircularQueueDeQueue(MyCircularQueue* obj);//删除
int myCircularQueueFront(MyCircularQueue* obj);//显示头
int myCircularQueueRear(MyCircularQueue* obj);//显示尾
void myCircularQueueFree(MyCircularQueue* obj);//释放
5.具体操作的代码实现
5.1创建一个顺序表
typedef struct
{
int* a;
int front;
int rear;
int k;
} MyCircularQueue;
//使用malloc函数开辟环状顺序表所需空间
//realloc开辟额外空间结局假溢出问题
MyCircularQueue* myCircularQueueCreate(int k)
{
MyCircularQueue* obj0 = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
MyCircularQueue* obj = (MyCircularQueue*)realloc(obj0->a, (k + 1) * sizeof(MyCircularQueue));
obj->front = 0;
obj->rear = 0;
obj->k = k;
return obj;
}5.2判空与判满操作
//判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj)
{
return obj->front == obj->rear;
}
//判满
bool myCircularQueueIsFull(MyCircularQueue* obj)
{
return (obj->rear + 1) % obj->k + 1 == obj->front;
}
5.3队尾加入新元素操作
//入
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{
if (myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->rear] = value;
obj->rear++;
obj->rear = (obj->rear) % obj->k + 1;
return true;
}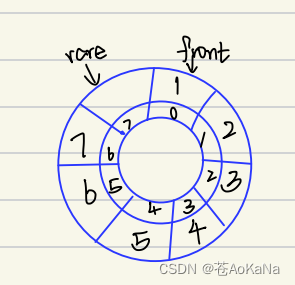
注:rear指向队尾元素的下⼀个位置
问题:循环数组最后⼀个空间是为了解决假栈溢出是不放元素的,如果数组 满了rare指向如图所示位置,再进⾏下⼀次放⼊元素的操作时它不就直接被 if(myCircularQueueIsFull(obj))驳回了 就不存在rare⽐k+1⼤的情况了 为啥 这⾥还要⽤obj->rear = (obj->rear) % obj->k + 1进⾏范围限制呢?
回答:判断队列是否满和⽤取模限定范围这两个操作是⼆选⼀,但是为了 保证代码的健壮性,所以最好两个都写
5.4队头删除元素操作
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{
if (myCircularQueueIsEmpty(obj))
{
return false;
}
free(obj->a[obj->front]);
obj->front++;
obj->front = (obj->front) % obj->k+1;//要考虑front在尾巴的情况
return true;
}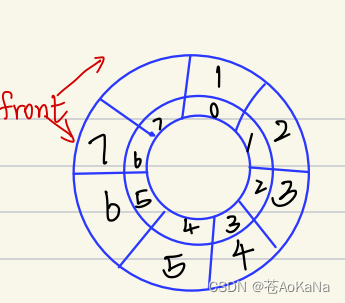
注:如图:front在尾巴时,此时front为7,进⾏⼀次删除操作后,front会变成8,但是 这个循环队列没有下标为8的元素,不在范围内,我们预期的是此时front为0,所以 ⽤取模obj->front = (obj->front) % obj->k+1进⾏范围限制操作
5.5显示头操作
//显示头
int myCircularQueueFront(MyCircularQueue* obj)
{
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->front];
}
}
5.6重难点:显示尾操作
int myCircularQueueRear(MyCircularQueue* obj)
{
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->rear - 1 + obj->k+1] % obj->k+1;
}
}
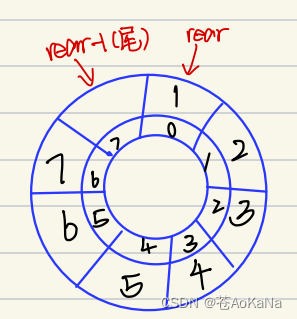
解析:
因为rear是指向队尾下⼀个位置,所以只有rear-1才是队尾 rear!=0时rear-1是没有任何问题的
但是,如果rear=0时,rear-1=-1,不在这个范围内
所以这个问题要分为rear=0和rear!=0两种情况进⾏分类讨论
1.rear!=0时
直接是(rear-1)%(k+1),当A%B是,如果a[obj->rear - 1] % obj->k+1;
2.rear=0时
按循环链表的逻辑lai讲,rear-1=7,于是乎代数上,我们⽤rear-1+k-1=7, 但是如果rear不是0,⼜会发⽣超出范围的情况,我们可以%(k+1)
如此,将两种情况归纳⼀下,就是 return obj->a[obj->rear - 1 + obj- >k+1] % obj->k+1;
当然,如果嫌这么写太别扭,两种情况也可以⽤if...else语句拆开直⽩地 分情况写
6.写这条题目时顺便把自己的思路写了一下整理成笔记,分享一下