初阶数据结构：二叉树（补充扩展）

news2024/9/23 19:25:05

目录

  • 1. 堆排序
    • 1.1补充：建堆的时间复杂度
    • 1.2 堆排序：升序与降序
  • 2. TopK问题
  • 3. 二叉树的链式结构及其遍历方式
    • 3.1 二叉树的链式结构
    • 3.2 二叉树的前序遍历
    • 2.2 二叉树的中序遍历
    • 2.3 后序遍历
    • 2.4 层序遍历
  • 4. 二叉树OJ练习
    • 4.1 单值二叉树
    • 4.2 判断两棵二叉树是否相等
    • 4.3 判断对称二叉树
    • 4.4 另一棵二叉树的子树
    • 4.5 二叉树的构建与销毁
    • 4.6 判断二叉树是否为完全二叉树
    • 4.7 补充练习
      • 4.7.1 二叉树的节点数
      • 4.7.2 二叉树的叶子节点数
      • 4.7.3 二叉树的第K层结点数
      • 4.7.4 查找二叉树中为x值的结点

1. 堆排序

1.1补充：建堆的时间复杂度

这里使用满二叉树近似计算，向下调整法建堆的时间复杂度：

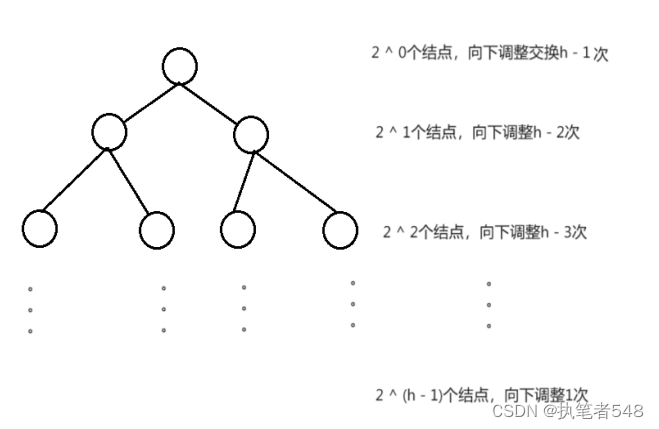
在这里插入图片描述

等比数列求和，得需调整n - log(n + 1)，时间复杂度为O(n)

1.2 堆排序：升序与降序

思路：我们先建堆，然后将堆顶（堆顶元素总是为最大或最小）的元素与尾部元素交换，size–，然后向下调整，直至堆为空。

  1. 排升序，建大堆（大堆的父亲结点都大于小堆）
  2. 排降序，建小堆

代码实现如下：

void HeapAdjustDown(int* arr, int n, int parent)
{
	//n为元素个数
	int child = parent * 2 + 1;

	while (child < n)
	{
		if (child + 1 < n && arr[child] < arr[child + 1])
		{
			child++;
		}

		if (arr[parent] < arr[child])
		{
			swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

int arr[] = { 27,15,18,28,34,65,49,25,37 };
//向下调整建堆
int n = sizeof(arr) / sizeof(arr[0]);
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
	HeapAdjustDown(arr, n, i);
}

ArrPrint(arr, n);

//交换首尾元素，size--，再向下调整
int size = n;
while (size)
{
	swap(&arr[0], &arr[size - 1]);
	size--;
	HeapAdjustDown(arr, size, 0);
}

2. TopK问题

当数据量很大时，且为乱序，数据无法一下全部加载到内存中，所以整体排序无法得出最大或最小的前K个数，那么，如何快速得出前K个最大/最小数。

思路：
先于数据首部建一个大小为K的

  1. 得出最大，建小堆
  2. 得出最小，建大堆

然后，再将剩余的N- K个数据与堆顶元素比较

  1. 当需要最大的数时，若比较元素大于堆顶元素，则交换二者再进行向下调整。
  2. 当需要最小的数时，若比较元素小于堆顶元素，则交换二者再进行向下调整。
void HeapAdjustDown2(int* arr, int n, int parent)
{
	//n为元素个数
	int child = parent * 2 + 1;

	while (child < n)
	{
		if (child + 1 < n && arr[child] > arr[child + 1])
		{
			child++;
		}

		if (arr[parent] > arr[child])
		{
			swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void TopK(int* arr, int k, int n)
{
	//筛选k个最大的数
	//在数据顶部建一个大小为k的小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		HeapAdjustDown2(arr, k, i);
	}

	//若遍历到大于堆顶的元素，交换并向下调整
	for (int j = k; j < n; j++)
	{
		if (arr[j] > arr[0])
		{
			swap(&arr[j], &arr[0]);
			HeapAdjustDown2(arr, k, 0);
		}
	}
}

3. 二叉树的链式结构及其遍历方式

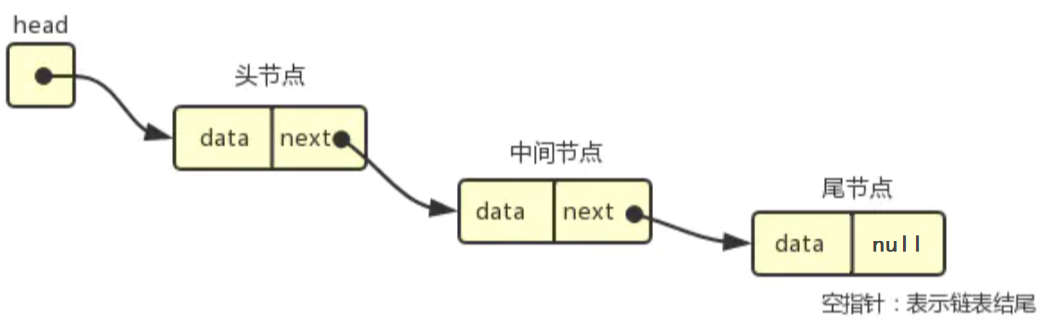
3.1 二叉树的链式结构

在前面的学习中，我们已经了解到，二叉树的结构由三部分组成根，左子树，右子树。

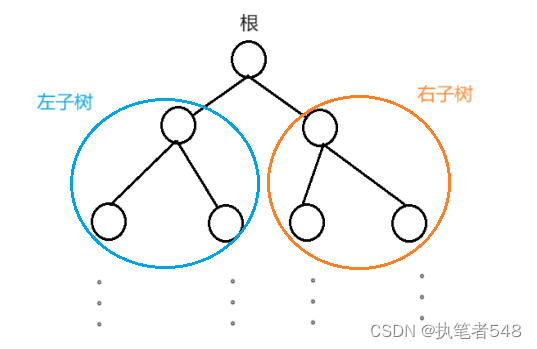
在这里插入图片描述

当我们使用链式存储的方式构建二叉树时，其结点的结构定义如下：

typedef struct TreeNode
{
	int val;
	//左子树指针
	struct TreeNode* left;
	//右子树指针
	struct TreeNode* right;
}

根据逻辑遍历的方式顺序不同，二叉树的遍历方式分为四种：前序，中序，后序，层序

3.2 二叉树的前序遍历

  1. 遍历逻辑顺序：根结点，左子树，右子树（根左右）
  2. 题目链接：
    前序遍历
void preorder_part(struct TreeNode* root, int* arr, int* size)
{
    if(root == NULL)
    {
        return;
    }

    arr[*size] = root->val;
    (*size)++;
    preorder_part(root->left, arr, size);
    preorder_part(root->right, arr, size);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    //根左右
    //为空树时，不反回空指针
    //返回数组
    
    *returnSize = 0;
    int* arr = (int*)malloc(100 * sizeof(int));
    preorder_part(root, arr, returnSize);

    return arr;
}

2.2 二叉树的中序遍历

  1. 遍历逻辑顺序：左根右
  2. 题目链接：
    中序遍历
void inorder_part(struct TreeNode* root, int* arr, int* size)
{
    if(root == NULL)
    {
        return;
    }

    inorder_part(root->left, arr, size);
    arr[*size] = root->val;
    (*size)++;
    inorder_part(root->right, arr, size);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = 0;
    int* arr = (int*)malloc(100 * sizeof(int));
    inorder_part(root, arr, returnSize);

    return arr;    
}

2.3 后序遍历

  1. 遍历逻辑顺序：左右根
  2. 题目链接：
    后序遍历
void postorder_part(struct TreeNode* root, int* arr, int* size)
{
    if(root == NULL)
    {
        return;
    }

    postorder_part(root->left, arr, size);
    postorder_part(root->right, arr, size);
    arr[*size] = root->val;
    (*size)++;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = 0;
    int* arr = (int*)malloc(100 * sizeof(int));
    postorder_part(root, arr, returnSize);

    return arr;        
}

2.4 层序遍历

遍历逻辑：依次按层进行遍历（利用队列存储子节点）

void LevelOrder(TreeNode* root)
{
	Queue q1;
	QueueInit(&q1);
	QueuePush(&q1, root);

	TreeNode* top = QueueFront(&q1);
	
	while (!QueueEmpty(&q1))
	{
		if (top)
		{
			QueuePush(&q1, top->left);
			QueuePush(&q1, top->right);
		}
		
		if (top)
		{
			printf("%c ", top->val);
		}
		else
		{
			printf("NULL ");
		}

		QueuePop(&q1);
		if (!QueueEmpty(&q1))
		{
			top = QueueFront(&q1);
		}
	}
}

4. 二叉树OJ练习

4.1 单值二叉树

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    单值二叉树
  3. 思路：任选一种遍历方式遍历整个二叉树，同时判断左右孩子结点的值等于父亲结点的值
bool isUnivalTree(struct TreeNode* root) 
{
    if(root == NULL)
    {
        return true;
    }

    if(root->left && root->val != root->left->val)
    {
        return false;
    }

    if(root->right && root->val != root->right->val)
    {
        return false;
    }
    
    return isUnivalTree(root->left) && isUnivalTree(root->right);    
}

4.2 判断两棵二叉树是否相等

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    判断两颗二叉树是否相等
    3 . 思路：按同样顺序遍历两棵树，同时判断
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    //调整逻辑顺序，不出现越界情况
    //二者都为NULL
    if(p == NULL && q == NULL)
    {
        return true;
    }

    //有一个为NULL
    if(p && q == NULL)
    {
        return false;
    }

    if(q && p == NULL)
    {
        return false;
    }

    //都不为NULL
    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

4.3 判断对称二叉树

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    对称二叉树
  3. 思路：按照对称的遍历方式，遍历判断二叉树的左右子树
bool order_part(struct TreeNode* left, struct TreeNode* right)
{
    if(left == NULL && right == NULL)
    {
        return true;
    }

    if(left && right == NULL)
    {
        return false;
    }

    if(right && left == NULL)
    {
        return false;
    }

    if(left->val != right->val)
    {
        return false;
    }

    return order_part(left->left, right->right) && order_part(left->right, right->left);
}

bool isSymmetric(struct TreeNode* root) 
{
    
    return order_part(root->left, root->right);
}

4.4 另一棵二叉树的子树

1.题目信息：
在这里插入图片描述
2. 题目链接：
另一颗树的子树
3. 思路：遇到与配对子树的根节点相同的结点即开始配对，直至遍历完整个树。
4. 注：将逻辑，语言转换（翻译）为代码

bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    //调整逻辑顺序，不出现越界情况
    //二者都为NULL
    if(p == NULL && q == NULL)
    {
        return true;
    }

    //有一个为NULL
    if(p && q == NULL)
    {
        return false;
    }

    if(q && p == NULL)
    {
        return false;
    }

    //都不为NULL
    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root == NULL)
    {
        return false;
    }

    if(root->val == subRoot->val && isSameTree(root, subRoot))
    {
        return true;
    }

    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

4.5 二叉树的构建与销毁

  1. 题目信息:
    在这里插入图片描述
  2. 题目链接：
    二叉树的构建与遍历
  3. 先创建根结点，再依次创建左子树，右子树
typedef struct TreeNode
{
    char val;
    struct TreeNode* left;
    struct TreeNode* right;
}TreeNode;

void inorder_part(struct TreeNode* root, char* arr, int* size)
{
	if (root == NULL)
	{
		return;
	}

	inorder_part(root->left, arr, size);
	arr[*size] = root->val;
	(*size)++;
	inorder_part(root->right, arr, size);
}

char* inorderTraversal(struct TreeNode* root, int* returnSize)
{
	//根左右
	//为空树时，不反回空指针
	//返回数组

	*returnSize = 0;
	char* arr = (char*)malloc(100 * sizeof(int));
	inorder_part(root, arr, returnSize);

	return arr;
}

TreeNode* BuyTreeNode(char val)
{
	TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));
	
	newnode->val = val;
	newnode->left = newnode->right = NULL;

	return newnode;
}

TreeNode* BinaryTreeCreate(char* a, int n, int* pi)
{
	TreeNode* root = NULL;

	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	if (a[*pi] != '#')
	{
		root = BuyTreeNode(a[*pi]);
	}
	(*pi)++;

	root->left = BinaryTreeCreate(a, n, pi);
	root->right = BinaryTreeCreate(a, n, pi);

	return root;
}

int main()
{
	char* a = (char*)malloc(100 * sizeof(char));
    char str;
    int count = 0;
    while(scanf("%c", &str) != EOF)
    {
        a[count++] = str;
    }

	int i = 0;
	TreeNode* root = BinaryTreeCreate(a, strlen(a), &i);
	
	int returnSize = 0;
	char* ret = inorderTraversal(root, &returnSize);

	for (int j = 0; j < returnSize; j++)
	{
		printf("%c ", ret[j]);
	}

    return 0;
}

二叉树的销毁：

void BinaryTreeDestory(TreeNode* root)
{
	//后序遍历
	if (root == NULL)
	{
		return;
	}

	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

4.6 判断二叉树是否为完全二叉树

思路：使用层序遍历，如果出现NULL后，又出现非NULL指针，那么此树就不是完全二叉树，反之，则是。

int BinaryTreeComplete(TreeNode* root)
{
	//层序遍历判断是否为完全二叉树
	Queue q1;
	QueueInit(&q1);
	QueuePush(&q1, root);

	TreeNode* top = QueueFront(&q1);
	//标志有NULL指针出现
	int count = 0;

	while (!QueueEmpty(&q1))
	{
		if (top)
		{
			QueuePush(&q1, top->left);
			QueuePush(&q1, top->right);
		}
		
		if (top == NULL)
		{
			count++;
		}

		if (count && top)
		{
			return 0;
		}

		QueuePop(&q1);
		if (!QueueEmpty(&q1))
		{
			top = QueueFront(&q1);
		}
	}

	return 1;
}

4.7 补充练习

4.7.1 二叉树的节点数

// 二叉树节点个数
int BinaryTreeSize(TreeNode* root)
{
	//根结点 + 左子树结点 + 右子树结点

	if (root == NULL)
	{
		return 0;
	}

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

4.7.2 二叉树的叶子节点数

// 二叉树叶子节点个数
int BinaryTreeLeafSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

4.7.3 二叉树的第K层结点数

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(TreeNode* root, int k)
{
	if (k == 0)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

4.7.4 查找二叉树中为x值的结点

// 二叉树查找值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, char x)
{
	//没找到
	if (root == NULL)
	{
		return NULL;
	}
	
	//找到了
	if (root->val == x)
	{
		return root;
	}
	
	//在左侧找
	TreeNode* left = BinaryTreeFind(root->left, x);
	//在右侧找
	TreeNode* right = BinaryTreeFind(root->right, x);
	
	if (left)
	{
		return left;
	}

	return right;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1490263.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

“零碳未来”：引领全球向低碳经济转型

“零碳未来”：引领全球向低碳经济转型

全球环境基金(GEF),这个由183个国家和地区组成的国际合作组织,是世界银行1990年创建的实验项目,一直致力于支持环境友好型项目,推动全球环境改善。而“零碳未来”不仅是一个由全球环境基金(GEF)创建的跨越国界的全新交易平台,更是一个致力于推动全球向低碳经济转型的零碳排放生…
阅读更多...
代码随想录day12（2）字符串：重复的子字符串（leetcode459）

代码随想录day12（2）字符串：重复的子字符串（leetcode459）

题目要求&#xff1a;给定一个非空的字符串&#xff0c;判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母&#xff0c;并且长度不超过10000。 思路&#xff1a; 一、首先对于暴力解法&#xff0c;可以枚举所有的字串进行判断。但是枚举时实际上只需…
阅读更多...
【Pytorch 第四讲】图像分类的Tricks

【Pytorch 第四讲】图像分类的Tricks

1. 标签平滑 在分类问题中&#xff0c;最后一层一般是全连接层&#xff0c;然后对应标签的one-hot编码&#xff0c;即把对应类别的值编码为1&#xff0c;其他为0。这种编码方式和通过降低交叉熵损失来调整参数的方式结合起来&#xff0c;会有一些问题。这种方式会鼓励模型对不同…
阅读更多...
【机器学习】生成对抗网络GAN

【机器学习】生成对抗网络GAN

概述 生成对抗网络&#xff08;Generative Adversarial Network&#xff0c;GAN&#xff09;是一种深度学习模型架构&#xff0c;由生成器&#xff08;Generator&#xff09;和判别器&#xff08;Discriminator&#xff09;两部分组成&#xff0c;旨在通过对抗训练的方式生成逼…
阅读更多...
在全志V853平台上成功部署深度学习步态识别算法

在全志V853平台上成功部署深度学习步态识别算法

北理工通信课题组辛喆同学在本科毕业设计《基于嵌入式系统的步态识别的研究》中&#xff0c;成功将深度步态识别算法GaitSet移植到全志V853开发板上。本研究在CASIA-B数据集上进行测试&#xff0c;正常行走状态下该系统的步态识别准确率达到了94.9%&#xff0c;背包行走和穿外套…
阅读更多...
Java I/O流

Java I/O流

一、常用文件操作 1.创建文件对象 2.获取文件相关信息 3.目录的操作和文件删除 二、IO 流原理及流的分类 1.IO流原理 2.流的分类 2.1 字节流和字符流 2.2 节点流和处理流 3.IO流体系图 三、常用的类介绍 1.FileInputStream 和 FileOutputStream&#xff08;字节流、节点流&…
阅读更多...
2核4g服务器能支持多少人访问？并发数性能测评

2核4g服务器能支持多少人访问？并发数性能测评

2核4g服务器能支持多少人访问&#xff1f;支持80人同时访问&#xff0c;阿腾云使用阿里云2核4G5M带宽服务器&#xff0c;可以支撑80个左右并发用户。阿腾云以Web网站应用为例&#xff0c;如果视频图片媒体文件存储到对象存储OSS上&#xff0c;网站接入CDN&#xff0c;还可以支持…
阅读更多...
力扣经典题目解析--反转链表

力扣经典题目解析--反转链表

原题地址: . - 力扣&#xff08;LeetCode&#xff09; 给你单链表的头节点 head &#xff0c;请你反转链表&#xff0c;并返回反转后的链表。 示例 1&#xff1a; 输入&#xff1a;head [1,2,3,4,5] 输出&#xff1a;[5,4,3,2,1] 题目解析 链表&#xff08;Linked List&…
阅读更多...
交叉编译qt5.14.2

交叉编译qt5.14.2

qt源码下载地址&#xff1a;qt-everywhere-src-5.14.2.tar.xz 1.修改qt-everywhere-src-5.14.2/qtbase/mkspecs/linux-arm-gnueabi-g/qmake.conf文件&#xff1a; # # qmake configuration for building with arm-linux-gnueabi-g #MAKEFILE_GENERATOR UNIX CONFIG …
阅读更多...
贪心算法练习题（最小化战斗力差距、谈判、纪念品分组、分糖果）

贪心算法练习题（最小化战斗力差距、谈判、纪念品分组、分糖果）

目录 一、贪心算法的介绍 二、贪心算法的实现步骤 三、最小化战斗力差距 四、谈判 五、纪念品分组 六、分糖果 一、贪心算法的介绍 贪心的基本原理:每一步都选择局部最优解&#xff0c;而尽量不考虑对后续的影响&#xff0c;最终达到全局最优解。 贪心的局限性:贪心算法…
阅读更多...
深度学习-Pytorch实现经典AlexNet网络：山高我为峰

深度学习-Pytorch实现经典AlexNet网络：山高我为峰

深度学习-Pytorch实现经典AlexNet网络之山高我为峰 深度学习中&#xff0c;经典网络引领一波又一波的技术革命&#xff0c;从LetNet到当前最火的GPT所用的Transformer&#xff0c;它们把AI技术不断推向高潮。2012年AlexNet大放异彩&#xff0c;它把深度学习技术引领第一个高峰…
阅读更多...
智慧楼宇的心脏：E6000物联网主机

智慧楼宇的心脏：E6000物联网主机

智慧楼宇是指通过全面覆盖的感知设备和互联网技术&#xff0c;为建筑提供高效、舒适、安全、环保、可持续的智能化服务。 在科技快速发展的今天&#xff0c;智慧楼宇已经不再是遥不可及的梦想。而在这个梦想成真的过程中&#xff0c;物联网主机扮演着至关重要的角色。它如同智慧…
阅读更多...
JS逆向进阶篇【去哪儿旅行登录】【下篇-逆向Bella参数JS加密逻辑Python生成】

JS逆向进阶篇【去哪儿旅行登录】【下篇-逆向Bella参数JS加密逻辑Python生成】

目录&#xff1a; 每篇前言&#xff1a;引子——本篇目的1、 代码混淆和还原&#xff08;1&#xff09;单独替换&#xff1a;&#xff08;2&#xff09;整个js文件替换&#xff1a; 2、算法入口分析3、 深入分析&#xff08;0&#xff09;整体分析&#xff1a;&#xff08;1&am…
阅读更多...
软件应用，财务收支系统试用版操作教程，佳易王记录账单的软件系统

软件应用，财务收支系统试用版操作教程，佳易王记录账单的软件系统

软件应用&#xff0c;财务收支系统试用版操作教程&#xff0c;佳易王记录账单的软件系统 一、前言 以下软件操作教程以 佳易王账单记账统计管理系统V17.0为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 如上图&#xff0c;统计报表包含 收支汇…
阅读更多...
StarRocks实战——松果出行实时数仓实践

StarRocks实战——松果出行实时数仓实践

目录 一、背景 二、松果出行实时OLAP的演进 2.1 实时数仓1.0的架构 2.2 实时数仓2.0的架构 2.3 实时数仓3.0的架构 三、StarRocks 的引入 四、StarRocks在松果出行的应用 4.1 在订单业务中的应用 4.2 在车辆方向的应用 4.3 StarRocks “极速统一” 落地 4.4 StarRoc…
阅读更多...
Day25-进程管理核心知识1

Day25-进程管理核心知识1

Day25-进程管理核心知识1 1. CentOS7 软件包安装方式1.1 什么是源码包&#xff1f;1.2 为什么要源码包安装1.3 源码包如何获取1.4 编译安装源码包软件 2. 源码编译示例 下面通过编译Nginx来深入了解下源码包编译的过程。3. Linux 系统进程介绍3.1 什么是进程?3.2 进程/守护进程…
阅读更多...
【深度学习】脑部MRI图像分割

【深度学习】脑部MRI图像分割

案例4&#xff1a;脑部MRI图像分割 相关知识点&#xff1a;语义分割、医学图像处理&#xff08;skimage, medpy&#xff09;、可视化&#xff08;matplotlib&#xff09; 1 任务目标 1.1 任务简介 本次案例将使用深度学习技术来完成脑部MRI(磁共振)图像分割任务&#xff0c…
阅读更多...
【MySQL高级篇】06-MySQL架构篇

【MySQL高级篇】06-MySQL架构篇

第01章:Linux下MySQL的安装与使用 1.1 安装前说明 1.1.1 Linux系统及工具的准备 1.1.2 查看是否安装过MySQL 1.1.3 MySQL的卸载 systemctl status mysqld.service #查看mysql服务启停状态 Windows下my.ini文件&#xff0c;在linux下对应为my.cnf 1.2 MySQL的Linux版安…
阅读更多...
Docker的安装及MySQL的部署(CentOS版)

Docker的安装及MySQL的部署(CentOS版)

目录 1 前言 2 Docker安装步骤 2.1 卸载可能存在的旧版Docker 2.2 配置Docker的yum库 2.2.1 安装yum工具 2.2.2 配置Docker的yum源 2.3 安装Docker 2.4 启动和校验 2.5 配置镜像加速(使用阿里云) 2.5.1 进入控制台 2.5.2 进入容器镜像服务 2.5.3 获取指令并粘贴到…
阅读更多...
【go从入门到精通】go环境安装和第一个经典程序

【go从入门到精通】go环境安装和第一个经典程序

go下载和环境变量配置 下载地址 Go官网下载地址&#xff1a;https://golang.org/dl/All releases - The Go Programming Languagehttps://golang.org/dl/ 然后根据自己的系统环境来选择不同的安装包下载&#xff0c;下面我分别针对不同环境进行说明&#xff08;大家可以根据自…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023