大家好,我是 方圆。二分查找本质上是一个规模退化且固定规模减小一半的分治算法,它的 思路很简单,但细节是魔鬼。通常我们会认为二分查找的应用场景是数组有序(单调),但实际上它也能在无序数组中应用,限制二分法使用的并不是数组是否有序,而是 数据是否具有两段性,只要一段满足某个性质,另一段不满足某个性质,那么就可以使用二分法。
本篇内容我想带大家更好地理解二分查找,不再根据模版生搬硬套,也不再对条件判断中的等号云里雾里。如果大家想要找刷题路线的话,可以参考 Github: LeetCode。
1. 在有序数组中应用二分查找
我们以 704. 二分查找 为例,来看看我们常用的模板之间有什么不同。
双闭区间模板,错位终止
这个模版大家应该很熟悉,使用的是双闭区间,即 [left, right]:
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + right >> 1;
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
}
我们以数组 nums = {1, 2, 4, 5} 为例,来看看指针 left 和 right 在不同情况下如何变化:
查找不存在的中间值 3:

我们可以发现最终 left 和 right 的位置是错位的,我们称它为 错位终止,而且 left 索引值(目标值应该在的索引位置)恰好 等于数组中小于被查找值的数量。
我们再来看看其他情况是不是也具备这种现象。
查找不存在的最大值 6:
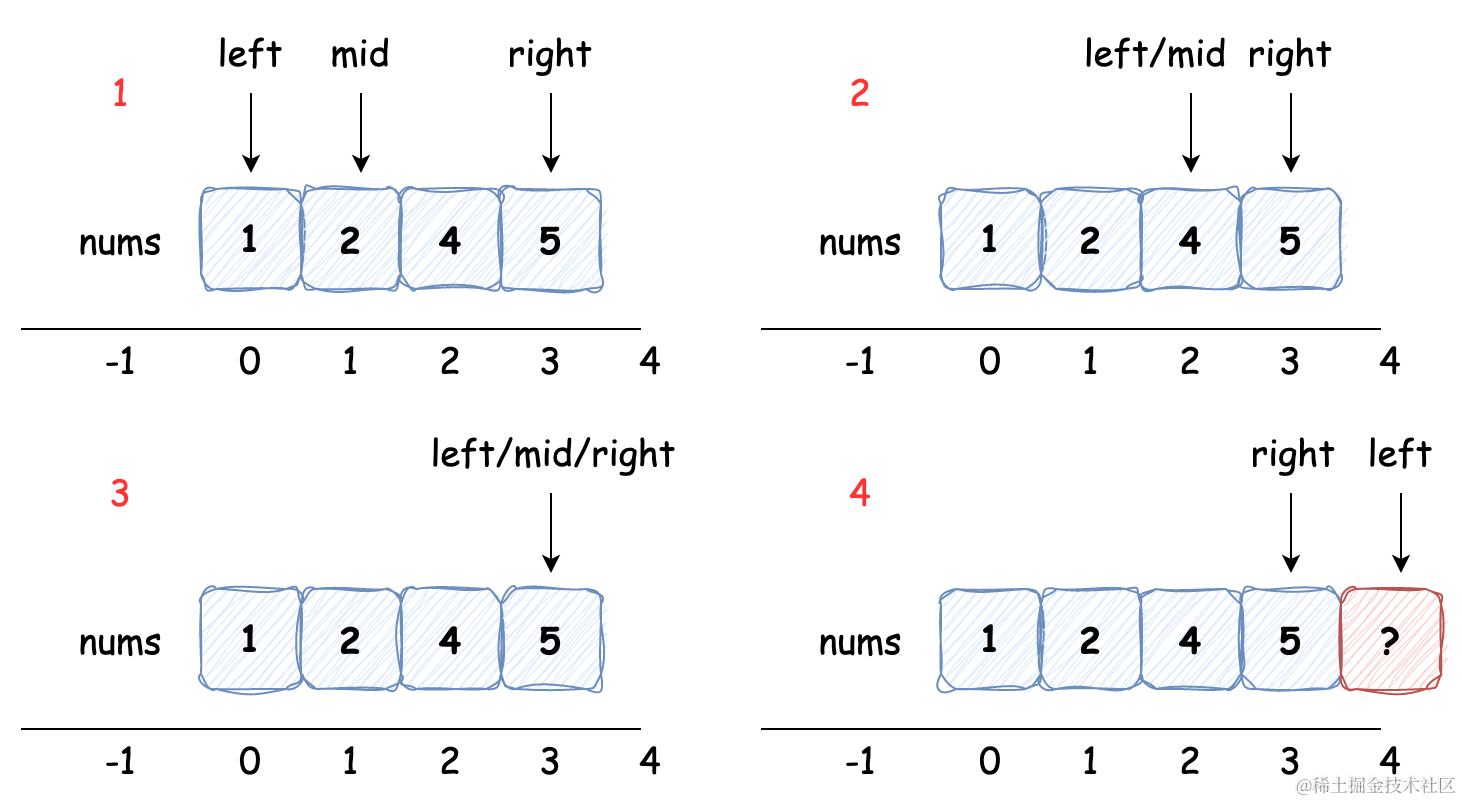
我们可以发现,如果查找的值比数组中所有的值都大的话,那么 right 指针的位置是始终不变的。我们仍能发现 left 索引值(目标值应该在的索引位置)为数组中小于被查找值的数量,终止时 left 和 right 错位。我们继续看下一种情况:
查找不存在的最小值 0:
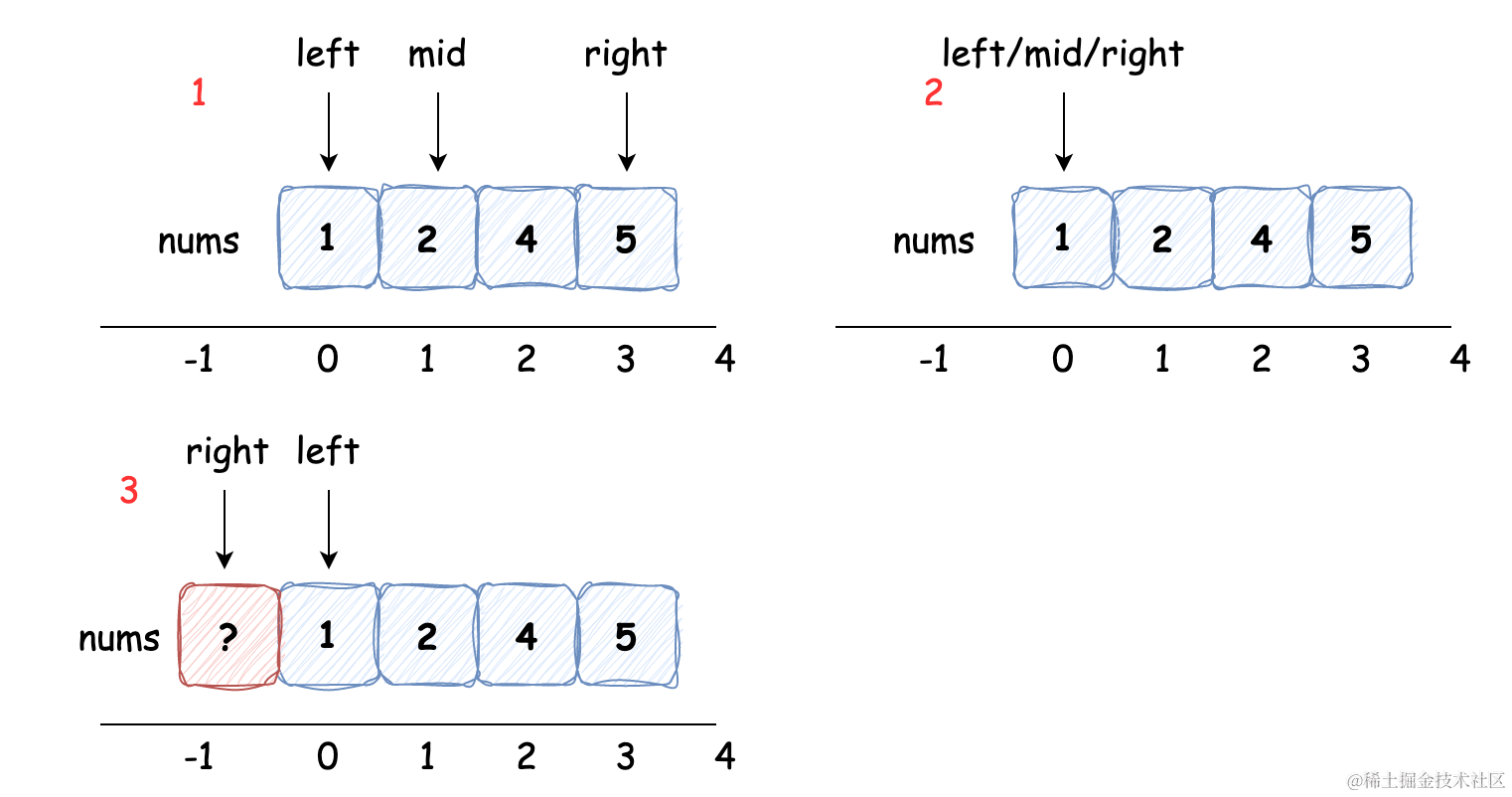
查找的值比数组中所有的值都小的话,我们发现 left 指针的位置是始终不变的,并且我们能够再次确认 left 索引值(目标值应该在的索引位置)为数组中小于被查找值的数量,终止时 left 和 right 错位。
我们根据现象考虑如下问题:
- 错位终止是不是因为 while 条件中的等号呢?如果我们把等号去掉是不是就能保证不错位终止而是等值终止呢?
显然错位终止并不取决于 while 条件中的等号,以在查找中间值 3 为例,left 和 right 没有出现等值的情况,即便我们去掉 while 条件中的等号它也会错位终止。虽然在后两种情况中有出现 left 和 right 等值的情况,但是如果我们此时选择终止循环,那么 left 的值便不能在所有情况下都具备表示数组中小于被查找值的数量的意义,所以在双闭模板中 while 条件的等号是不能随便去掉的。
左闭右开模板,等值终止
左闭右开区间模版如下,即 [left, right),注意其中 right 值在初始时为数组长度,不包含在有效索引范围内,且 while 条件中没有等号:
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + right >> 1;
if (nums[mid] > target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
}
我们仍然以数组 nums = {1, 2, 4, 5} 为例,来看看指针 left 和 right 在不同情况下如何变化:
查找不存在的中间值 3:

我们能发现结束循环时,left 和 right 是等值的,我们称这种情况为 等值终止,且 left 索引值(目标值应该在的索引位置)也正好 等于数组中小于被查找值的数量。
查找不存在的最大值 6:
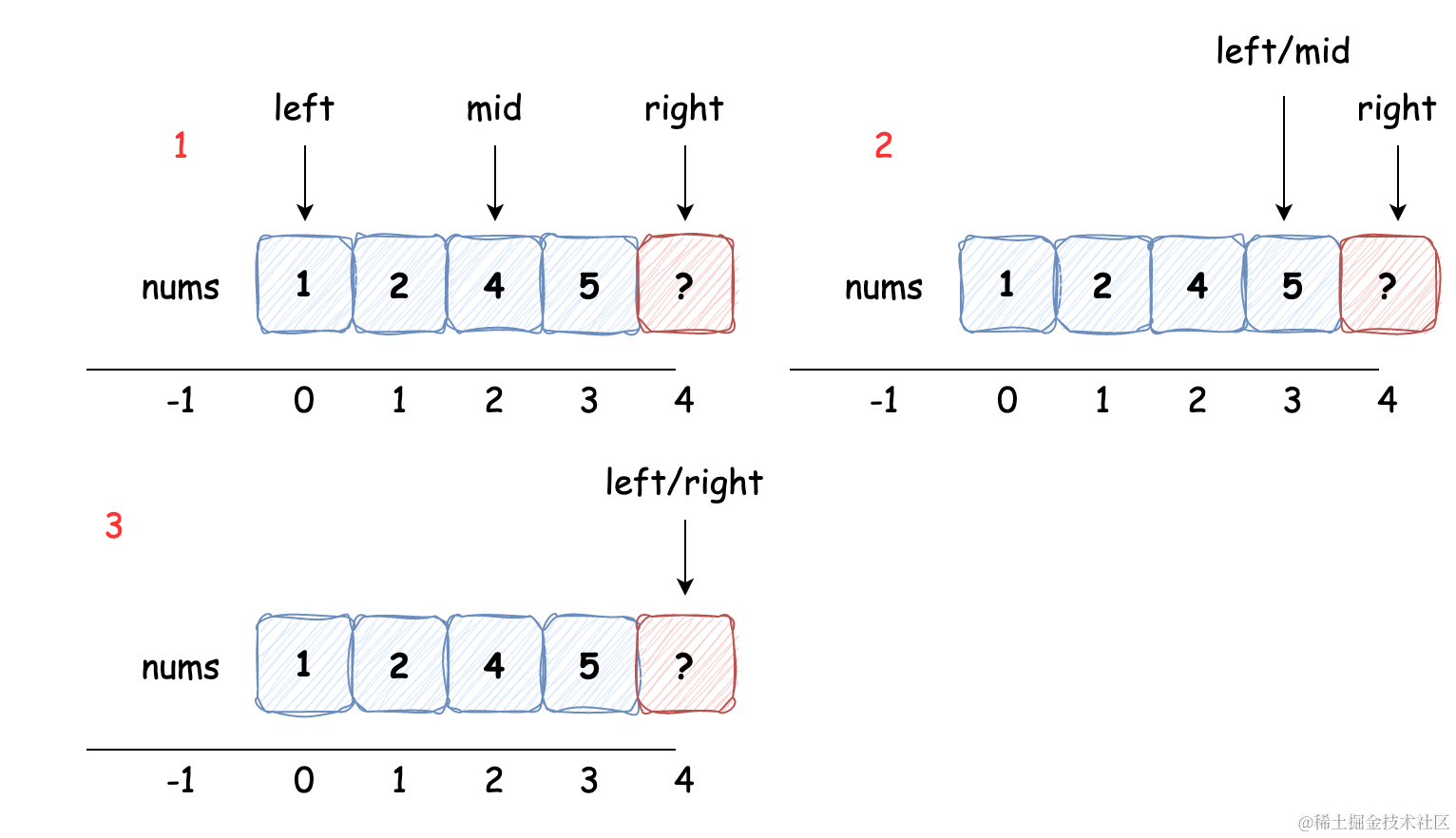
我们能够发现,如果查找的值比数组中所有的值都大的话,那么 right 指针的位置始终不变。而且我们仍能发现 left 索引值(目标值应该在的索引位置)为数组中小于被查找值的数量,终止时 left 和 right 等值。
查找不存在的最小值 0:

如果查找的值比数组中所有的值都小的话,那么 left 指针的位置始终不变,而且 left 索引值为数组中小于被查找值的数量,终止时 left 和 right 等值。
警惕在左闭右开模板的 while 条件中添加等号,因为这可能会造成死循环。以查找区间内不存在的最小值为例,它会涉及 right 指针不断变化,如果添加上等号条件,那么会一直循环在 right = mid 的逻辑里,left 和 right 一直相等导致无限循环
这两个模板对比下来,有四个方面值得我们关注:初始值、循环条件 和 指针更新语句。
mid计算方式在这两个模板中是相同的,所以我们在这里就不再延伸了,不同的是初始值、循环条件和指针更新语句。
-
双闭区间的初始值都是数组的最左端和最右端有效索引值,而左闭右开区间的 right 初始值为数组长度;
-
双闭区间的循环条件包含了等号(错位终止),而左闭右开区间的循环条件不包含等号(等值终止);
-
指针更新语句和初始值的定义以及区间有关系,在双闭区间模板中,两指针都包含在区间范围内,所以变化时会有加 1 或减 1 的操作,这样才能将不符合条件的范围排除在区间之外;而在左闭右开区间模板中,left 指针包含在区间范围内,所以变化时有加 1 操作,right 指针没有包含在区间范围内,所以它变换时更新成 mid 就代表了已经将不符合条件的范围排除在区间之外了。
这三个方面共同影响着二分查找是否正确以及是否会陷入到死循环,所以当我们确定要使用二分查找时,要先从这三个方面着手考虑。二分查找我认为本质上是 left 和 right 不断互相靠近的过程,循环条件决定循环结束时两指针的位置,mid 的计算方式和指针更新语句决定了数据规模如何变化。
相关练习
-
35. 搜索插入位置
-
367. 有效的完全平方数
这道题很有意思,根据题意,我们需要不断的枚举任何可能的值,直到找到或找不到返回结果值,二分查找很合适,如果 mid2 > num,那么证明 mid 及其右侧区间都不满足条件;如果 mid2 < num,那么证明 mid 及其左侧区间不满足条件。但是值得注意的是,由于本题我们要枚举的是数值本身,而不是索引,所以初始值 left 是从 1 开始,而不是从 0 开始。左闭右开区间模板题解如下:
public boolean isPerfectSquare(int num) {
int left = 1, right = num + 1;
while (left < right) {
int mid = left + right >> 1;
long val = (long) mid * mid;
if (val > num) {
right = mid;
} else if (val < num) {
left = mid + 1;
} else {
return true;
}
}
return false;
}
- 744. 寻找比目标字母大的最小字母
本题对二分查找的简单运用,数组有序,找到比 target 的字母,根据数据的两段性,那么必然存在一段大于 target,一段小于等于 target,需要注意不满足条件时取数组首位元素:
public char nextGreatestLetter(char[] letters, char target) {
int left = 0, right = letters.length;
while (left < right) {
int mid = left + right >> 1;
if (letters[mid] > target) {
right = mid;
} else {
left = mid + 1;
}
}
return left == letters.length ? letters[0] : letters[left];
}
-
34. 在排序数组中查找元素的第一个和最后一个位置
-
240. 搜索二维矩阵 II
-
911. 在线选举
-
1608. 特殊数组的特征值
-
剑指 Offer 53 - II. 0~n-1中缺失的数字
-
1818. 绝对差值和
-
33. 搜索旋转排序数组
-
153. 寻找旋转排序数组中的最小值
-
81. 搜索旋转排序数组 II
-
154. 寻找旋转排序数组中的最小值 II
33、153、81 和 154 题目类似,我们就拿最难的 154 题来做题解吧。以数组 [4, 5, 6, 7, 0, 1, 4] 为例,我们定义数组中 [4, 5, 6, 7] 为大区间,[0, 1, 4] 为小区间,如果我们想在其中找到最小值的话,那么我们就一定要去到小区间中才行,在这里理解起来肯定是没问题的,那么我们使用二分查找法该怎么判断当前区间是小区间还是大区间呢?
其实很简单:
-
如果
nums[mid] > nums[right]那么证明 mid 索引一定在大区间中,想回到小区间,则 left = mid + 1; -
如果
nums[mid] < nums[right]那么证明 mid 索引一定在小区间中,我们想在小区间中找最小值,则 right = mid,缩小范围即可,因为我们不确定 mid - 1 是否在小区间中,所以只能 right = mid;
不过这道题可不是难在这里,它难在了数组中存在 重复元素值,如果 nums[mid] == nums[right] ,那你说它是在大区间还是在小区间呢?这个时候我们就分不清了,所以在这里就不能再依靠二分查找法来缩小区间范围了,但是有一点是能确定的,我们想要找的值一定在区间 [left, right] 内,所以我们此时执行线性遍历即可,最后,题解如下,因为我们要使用 nums[right] 值,所以 right 初始值不能为 nums.length,防止越界,便使用了双闭区间模板:
public int findMin(int[] nums) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + right >> 1;
// 一定落在了大区间
if (nums[mid] > nums[right]) {
left = mid + 1;
continue;
}
// 一定落在了小区间
if (nums[mid] < nums[right]) {
right = mid;
continue;
}
// 相等的情况可能在大区间也可能在小区间,不过现在的答案一定在 [left, right] 区间内,所以遍历找一下即可
int min = nums[left];
for (int i = left + 1; i <= right; i++) {
min = Math.min(min, nums[i]);
}
return min;
}
return nums[left];
}
2. 无序数组中应用二分查找
查找峰值是二分查找在无序数组中的典型应用,我们以下面两题为例:
- 162. 寻找峰值
我觉得这道题第一次做还是比较难的,建议先看看【宫水三叶の相信科学系列】关于能够「二分」的两点证明题解,她讲的已经很清晰了。在这里附上我的答案:
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + right >> 1;
if (mid == nums.length - 1 || nums[mid] > nums[mid + 1]) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
与三叶的题解不同的是我没有定义初始值 right = nums.length - 1 ,而是考虑了如果数组最后一个元素是峰值的情况,添加了 mid == nums.length - 1 的条件判断(因为我实在写不出来 right = nums.length - 1 的初始值),因为题目中有 nums[n] 为负无穷,所以如果当 left 指针到达 nums.length - 1 的位置时,说明该位置必然为峰值。
- 852. 山脉数组的峰顶索引
3. 贪心算法结合二分查找的应用
像含有 最大值最小和最小值最大 和 求第 K 小 这些关键词的题目一般需要贪心算法结合二分查找来解题,它们相对来说比较困难。
我在刷了一些列题目之后,发现了能通过如下两点来求解:
-
要查找的对象就是 题目要求的结果值,那么我们需要将 left 和 right 的范围定义在结果值可能的区间范围内,即 left 表示可能的最小值,right 表示可能的最大值
-
二分查找的目的是为了加快枚举可能的结果值,在枚举每个结果值时要和题目要求的条件进行比较,确定满足条件和不满足条件时 left 和 right 指针如何变化
我们以如下题目为例来解释这两个特点:
- 1760. 袋子里最少数目的球
题目要求的结果值为袋子里球的数目,袋子里能装的球数最小为 1,最大值为当前袋子中球数的最大值,则:int left = 1, right = Arrays.stream(nums).max().getAsInt();
接下来再根据我们枚举到的某个球数,计算它需要的操作次数,当满足条件时,尝试缩小袋子内的球数;当不满足条件时,尝试扩大袋子内的球数。循环结束时即为满足条件的球数。
public int minimumSize(int[] nums, int maxOperations) {
int left = 1, right = Arrays.stream(nums).max().getAsInt();
while (left < right) {
int mid = left + right >> 1;
int op = 0;
for (int num : nums) {
op += (num - 1) / mid;
}
if (op > maxOperations) {
left = mid + 1;
} else {
right = mid;
}
}
return right;
}
- 875. 爱吃香蕉的珂珂
题目要求的是吃香蕉的速度,它的最小速度为 1,最大速度为香蕉堆内的最大值,则:int left = 1, right = Arrays.stream(piles).max().getAsInt() + 1;
接下来通过二分查找枚举速度并计算吃香蕉的时间,当不满足条件时,尝试扩大吃香蕉的速度;当满足条件时,尝试缩小吃香蕉的速度。在循环结束时,即为满足条件的结果值。
public int minEatingSpeed(int[] piles, int h) {
int left = 1, right = Arrays.stream(piles).max().getAsInt() + 1;
while (left < right) {
int mid = left + right >> 1;
int curHour = 0;
for (int pile : piles) {
curHour += pile / mid;
if (pile % mid > 0) {
curHour++;
}
}
if (curHour > h) {
left = mid + 1;
} else {
right = mid;
}
}
return right;
}
- 2226. 每个小孩最多能分到多少糖果
这道题我觉得很有意思,题目要求的是糖果数目,我们从示例中能发现糖果数目最小能取到 0,所以最初我在定义 left 和 right 的区间范围时,如下 int left = 0, right = Arrays.stream(candies).max().getAsInt() + 1;
如果这样取值,并采用左闭右开区间的二分查找,那么在计算若干糖果数目最多能分给多少个孩子的时候,会发生除以 0 的情况:
long children = 0;
for (int candy : candies) {
children += candy / mid;
}
为了避免这种情况,最小值要从 1 开始,即 int left = 1, right = Arrays.stream(candies).max().getAsInt() + 1;
接下来通过二分查找不断地枚举可能的糖果数目,当不满足条件时,尝试缩小糖果数目;当满足条件时,尝试扩大糖果数目。循环结束时,结果值为“刚好不满足条件的糖果数”,将结果值 left - 1 即为所求,而且这也覆盖到了糖果数为 0 的情况。
从这里我们也可以反推出 left 的最小取值,因为结束条件为刚好不满足条件的糖果数,它始终为比答案大 1,而我们要获取的结果值最小值为 0,刚好能够在 left 取 1 时覆盖到
public int maximumCandies(int[] candies, long k) {
int left = 1, right = Arrays.stream(candies).max().getAsInt() + 1;
while (left < right) {
int mid = left + right >> 1;
long children = 0;
for (int candy : candies) {
children += candy / mid;
}
if (children < k) {
right = mid;
} else {
left = mid + 1;
}
}
return left - 1;
}
- 1011. 在 D 天内送达包裹的能力
本题要求的是船最低运载能力,因为我们需要保证船能一天拉走最重的货物,所以 left 的取值为 weights 中最大值,而 right 的取值为所有 weights 元素的和,即能一天拉走所有货物的运载能力:
int left = 0, right = 1;
for (int weight : weights) {
left = Math.max(weight, left);
right += weight;
}
之后我们不断地枚举可能的运载能力,当满足条件时尝试缩小运载能;当不满足条件时尝试扩大运载能力。循环结束时结果值为刚好满足条件的运载能力。
public int shipWithinDays(int[] weights, int days) {
int left = 0, right = 1;
for (int weight : weights) {
left = Math.max(left, weight);
right += weight;
}
while (left < right) {
int mid = left + right >> 1;
int already = 0;
int day = 1;
for (int weight : weights) {
if (already + weight <= mid) {
already += weight;
} else {
day++;
already = weight;
}
}
if (day > days) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
- 410. 分割数组的最大值
本题和上题基本一致,不再多做解释:
public int splitArray(int[] nums, int m) {
int left = 0, right = 0;
for (int num : nums) {
left = Math.max(left, num);
right += num;
}
while (left < right) {
int mid = left + right >> 1;
int sum = 0;
int tempM = 0;
for (int num : nums) {
if (sum + num <= mid) {
sum += num;
} else {
tempM++;
sum = num;
}
}
if (sum > 0) {
tempM++;
}
if (tempM <= m) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
- 1552. 两球之间的磁力
题目要求的是磁力,最小磁力为 1,最大磁力为最大的位置减去最小的位置,即将 position 排序后最后一个元素减去第一个元素,所以 left 和 right 为:int left = 1, right = position[position.length - 1] - position[0] + 1;
之后我们需要将磁力和球数关联:最小磁力越大,能放置的球数越少,根据该条件我们可以控制二分查找的范围变化:当球数放不够的时候,将磁力缩小,即 right = mid ;当球数够的时候,我们需要将最小磁力变大以尝试更大的结果值,最终循环结束时,为“刚好”不够 m 个球的时候,将磁力缩小 1 便能满足条件了:
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
int left = 1, right = position[position.length - 1] - position[0] + 1;
while (left < right) {
int mid = left + right >> 1;
int pre = position[0];
int count = 1;
for (int i = 1; i < position.length; i++) {
if (position[i] - pre >= mid) {
pre = position[i];
count++;
}
}
if (count >= m) {
left = mid + 1;
} else {
right = mid;
}
}
return left - 1;
}
- 475. 供暖器
本题要求的是最小加热半径,因为当只需要只给某位置的房屋加热并且加热器与该房屋位置相同时是不需要加热半径的,所以最小半径为 0,根据题意最大半径为 1e9 - 1,则:int left = 0, right = (int) 1e9;
下面我们要枚举半径来判断其是否能覆盖所有的房屋:能覆盖的情况下,尝试缩小半径;不能覆盖的情况下,尝试放大半径。循环结束时,为刚好能够覆盖所有房屋的最小半径值。
public int findRadius(int[] houses, int[] heaters) {
Arrays.sort(houses);
Arrays.sort(heaters);
int left = 0, right = (int) 1e9;
while (left < right) {
int mid = left + right >> 1;
boolean cover = true;
int heaterIndex = 0;
for (int house : houses) {
while (heaterIndex < heaters.length && (heaters[heaterIndex] - mid > house || heaters[heaterIndex] + mid < house)) {
heaterIndex++;
}
if (heaterIndex == heaters.length) {
cover = false;
break;
}
}
if (cover) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
- 1802. 有界数组中指定下标处的最大值
解决这道题的前提是需要知道等差数列的求和公式为:(首项 + 尾项)* 项数 / 2,根据题意,我们需要求 index 处的最大值,可知其最小值为 1,最大值为 maxSum,则:int left = 1, right = maxSum + 1;
之后我们便需要不断地枚举值来判定它是否满足不超过 maxSum 的条件:当条件满足时尝试扩大最大值;当条件不满足时尝试缩小最大值。循环结束时为刚好不满足条件的最大值,将其减 1 即为所求。
public int maxValue(int n, int index, int maxSum) {
int left = 1, right = maxSum + 1;
while (left < right) {
int mid = left + right >> 1;
long sum = 0L;
sum += sum(mid, index + 1);
sum += sum(mid - 1, n - index - 1);
if (sum <= maxSum) {
left = mid + 1;
} else {
right = mid;
}
}
return left - 1;
}
/**
* 求和
*
* @param last 最后一项的值
* @param m 总的长度
*/
private long sum(int last, int m) {
long sum = 0L;
if (m < last) {
sum += (long) (last + last - m + 1) * m / 2;
} else {
sum += (long) (1 + last) * last / 2;
sum += (m - last);
}
return sum;
}
- 668. 乘法表中第k小的数
这道题是典型的第 K 小问题,我们从题意中可知,结果值的取值范围为 1 ~ m * n,则 int left = 1, right = m * n;
不过,我们该如何计算每个数值是第几小呢,先看看下图:

可知第 i 行的数都是 i 的倍数,那么我们用 5 除以当前行数便可以获取到它在该行小于等于它的数的数量,因为每行的数量被列数限制,所以我们要取列数和计算值中的小值。这样,我们就能够计算出 5 是第 6 小的数字了,之后与题目要求的 K 值做比较,如果比 6 比 K 大的话,我们需要移动 right 指针,否则移动 left 指针,题解如下:
public int findKthNumber(int m, int n, int k) {
int left = 1, right = m * n;
while (left <= right) {
int mid = left + right >> 1;
int count = 0;
for (int i = 1; i <= m; i++) {
count += Math.min(n, mid / i);
}
if (count >= k) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return left;
}
- 719. 找出第 K 小的数对距离
再来一道第 K 小问题吧,由题意可知,要求的是数对距离,根据题目中数组元素的取值条件可以得出数对的取值范围为 0 ~ 1e6,则 int left = 0, right = (int) 1e6 + 1;
计算某个值是数组范围内第几小的距离比较简单,采用双指针的方法计算每个值能到达的最右端的区间范围即可计算出当前数对距离是第几小,之后再根据与 K 值的比较来变换指针,题解如下:
public int smallestDistancePair(int[] nums, int k) {
Arrays.sort(nums);
int left = 0, right = (int) 1e6 + 1;
while (left < right) {
int mid = left + right >> 1;
int count = 0;
for (int i = 0, j = 1; i < nums.length; i++) {
while (j < nums.length && nums[j] - nums[i] <= mid) {
j++;
}
count += j - i - 1;
}
if (count >= k) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
巨人的肩膀
-
《算法 第四版》 第 3.1 章
-
二分查找从入门到入睡
-
不需要想那么复杂,几句话就给你说明白
-
「二分法+贪心思想」的应用