数据结构从入门到精通——链表

news2024/11/17 7:50:02

链表

  • 前言
  • 一、链表
    • 1.1 链表的概念及结构
    • 1.2 链表的分类
    • 1.3 链表的实现
    • 1.4 链表面试题
    • 1.5 双向链表的实现
  • 二、顺序表和链表的区别
  • 三、单项链表实现具体代码
    • text.h
    • text.c
    • main.c
    • 单链表的打印
    • 空间的开辟
    • 链表的头插、尾插
    • 链表的头删、尾删
    • 链表中元素的查找
    • 链表在指定位置之前、之后插入数据
    • 删除链表中的结点
    • 销毁链表
  • 四、双向循环链表代码的具体实现
    • text.h
    • text.c
    • main.c
    • 双向循环链表的创建
    • 双向循环链表的初始化
    • 双向循环链表的销毁
    • 双向循环链表的打印
    • 双向循环链表的头插和尾插
    • 双向循环链表的头删和尾删
    • 双向循环链表的元素查找
    • 双向循环链表的插入和删除

前言

链表是一种常见的数据结构，由一系列节点组成，每个节点包含数据和指向下一个节点的指针。链表的一个显著特点是，它不需要在内存中连续存储，因此可以高效地插入和删除节点。这种灵活性使得链表在许多应用中成为理想的选择，尤其是在需要动态调整数据结构大小的场景中。

在链表的实现中，通常会有头节点和尾节点之分。头节点是链表的第一个节点，而尾节点是链表的最后一个节点。通过遍历链表，我们可以访问链表中存储的所有数据。链表还支持在链表头部或尾部快速添加新节点，这些操作的时间复杂度通常为O(1)。

然而，链表也有一些缺点。比如，访问链表中的某个特定节点需要从头节点开始遍历，这导致访问链表中间节点的平均时间复杂度为O(n)。此外，链表需要额外的空间来存储指针，这增加了内存的使用。

链表有多种类型，如单向链表、双向链表和循环链表等。单向链表是最简单的链表类型，每个节点只有一个指向下一个节点的指针。双向链表则允许节点同时指向前一个和下一个节点，这使得双向链表在某些操作上比单向链表更高效。循环链表则是将尾节点的指针指向头节点，形成一个闭环。

在实际应用中，链表常用于实现栈、队列和哈希表等数据结构。例如，链表可以作为栈的底层数据结构，实现元素的先进后出。此外，链表还可以用于实现动态数组，支持元素的动态插入和删除。

总之，链表作为一种重要的数据结构，在编程和数据处理中发挥着重要作用。尽管链表在某些方面存在不足，但其灵活性和高效性使得它在许多场景中仍然是理想的选择。通过深入了解链表的特性和应用，我们可以更好地利用这种数据结构来解决实际问题。

一、链表

1.1 链表的概念及结构

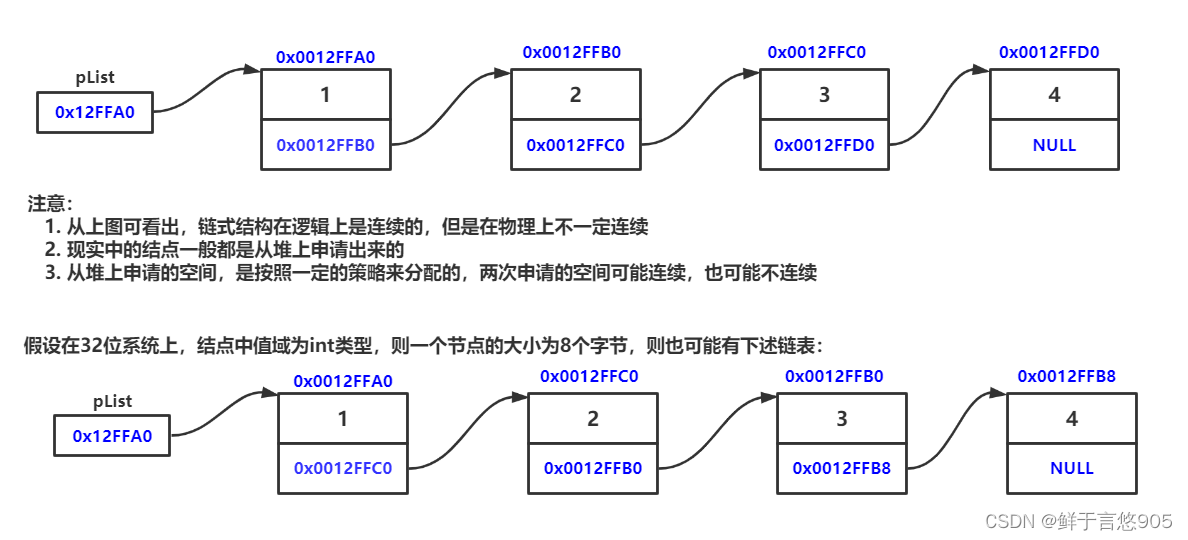
概念：链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表
中的指针链接次序实现的 。
在这里插入图片描述
在这里插入图片描述
现实中 数据结构中
在这里插入图片描述

1.2 链表的分类

实际中链表的结构非常多样，以下情况组合起来就有8种链表结构：

  1. 单向或者双向
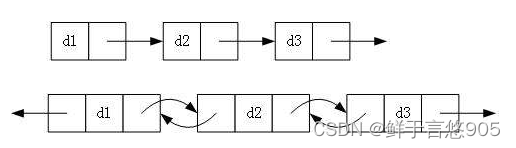
    在这里插入图片描述
  2. 带头或者不带头
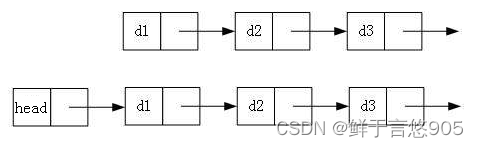
    在这里插入图片描述
  3. 循环或者非循环
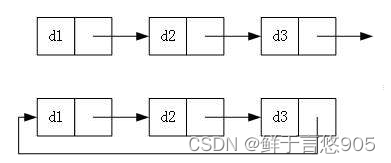
    在这里插入图片描述

虽然有这么多的链表的结构，但是我们实际中最常用还是两种结构：
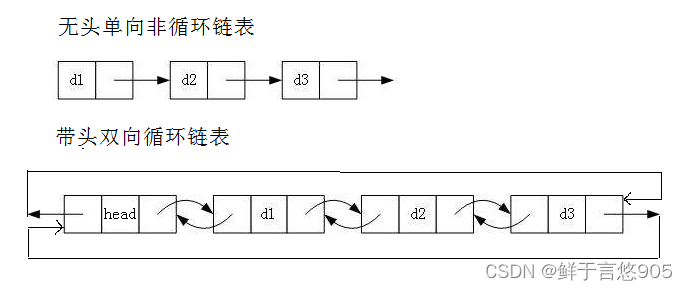
在这里插入图片描述

  1. 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结
    构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
  2. 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都
    是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带
    来很多优势，实现反而简单了，后面我们代码实现了就知道了。

1.3 链表的实现

// 1、无头+单向+非循环链表增删查改实现
typedef int SLTDateType;
typedef struct SListNode
{
 SLTDateType data;
 struct SListNode* next;
}SListNode;
// 动态申请一个结点
SListNode* BuySListNode(SLTDateType x);
// 单链表打印
void SListPrint(SListNode* plist);
// 单链表尾插
void SListPushBack(SListNode** pplist, SLTDateType x);
// 单链表的头插
void SListPushFront(SListNode** pplist, SLTDateType x);
// 单链表的尾删
void SListPopBack(SListNode** pplist);
// 单链表头删
void SListPopFront(SListNode** pplist);
// 单链表查找
SListNode* SListFind(SListNode* plist, SLTDateType x);
// 单链表在pos位置之后插入x
// 分析思考为什么不在pos位置之前插入？
void SListInsertAfter(SListNode* pos, SLTDateType x);
// 单链表删除pos位置之后的值
// 分析思考为什么不删除pos位置？
void SListEraseAfter(SListNode* pos);

1.4 链表面试题

  1. 删除链表中等于给定值 val 的所有结点
  2. 反转一个单链表
  3. 给定一个带有头结点 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则
    返回第二个中间结点
  4. 输入一个链表，输出该链表中倒数第k个结点
  5. 将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有
    结点组成的
  6. 编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结
    点之前
  7. 链表的回文结构
  8. 输入两个链表，找出它们的第一个公共结点
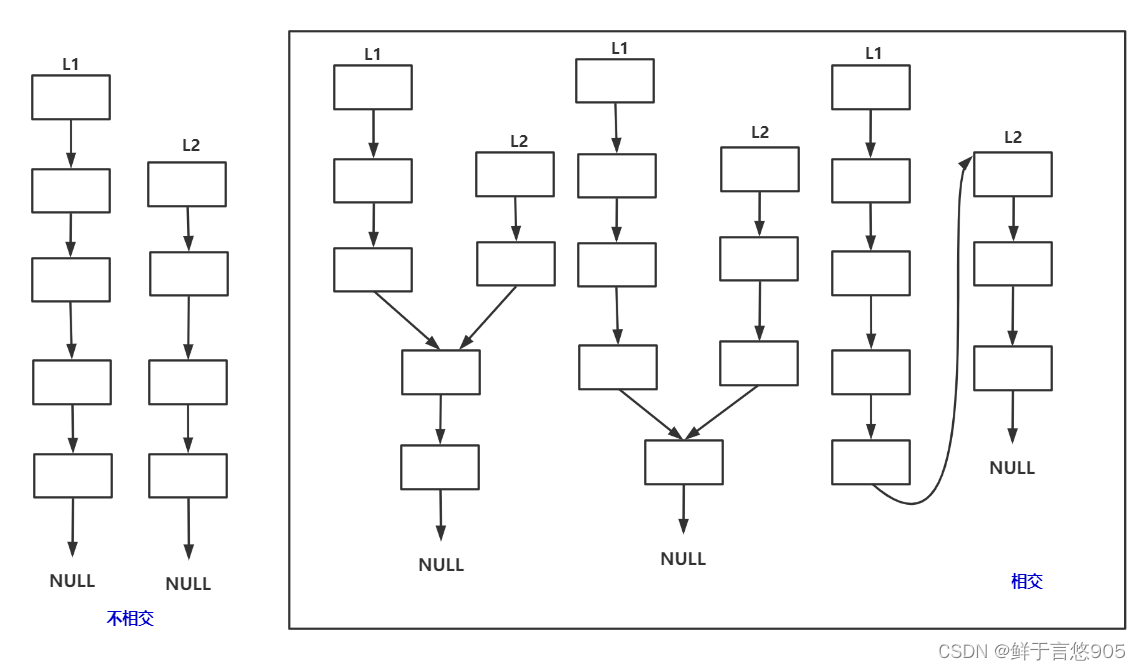
    在这里插入图片描述
  9. 给定一个链表，判断链表中是否有环
    【思路】
    快慢指针，即慢指针一次走一步，快指针一次走两步，两个指针从链表其实位置开始运行，如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。比如：陪女朋友到操作跑步减肥。

【扩展问题】

  • 为什么快指针每次走两步，慢指针走一步可以？
    假设链表带环，两个指针最后都会进入环，快指针先进环，慢指针后进环。当慢指针刚进环时，可能就和快指针相遇了，最差情况下两个指针之间的距离刚好就是环的长度。
    此时，两个指针每移动一次，之间的距离就缩小一步，不会出现每次刚好是套圈的情况，因此：在满指针走到一圈之前，快指针肯定是可以追上慢指针的，即相遇。

  • 快指针一次走3步，走4步，…n步行吗？
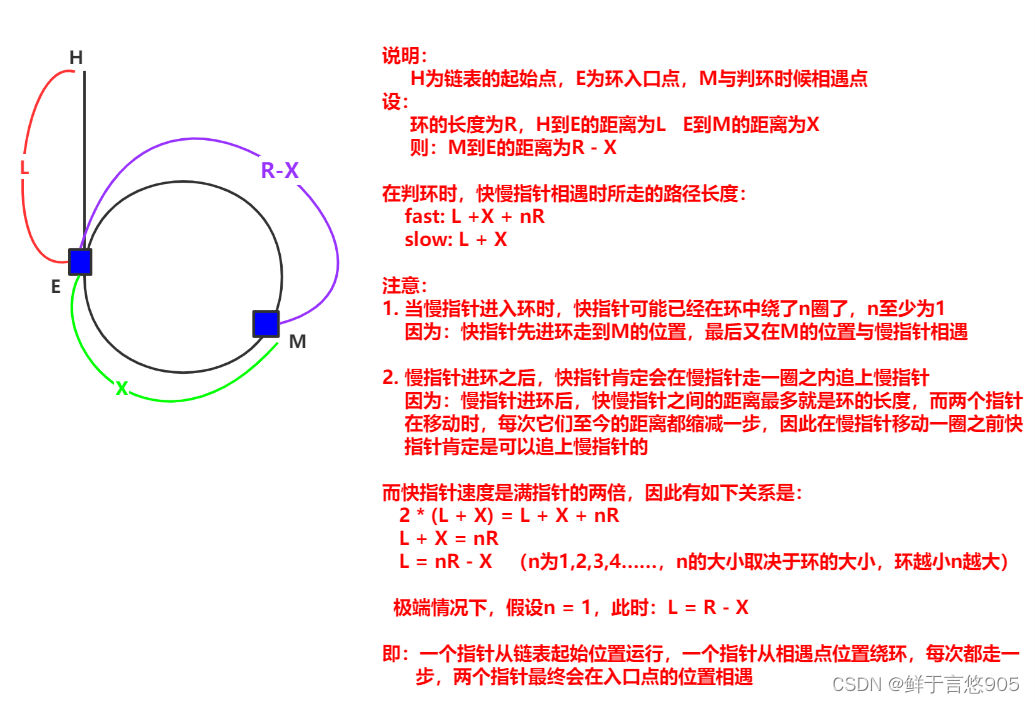
    在这里插入图片描述

  1. 给定一个链表，返回链表开始入环的第一个结点。 如果链表无环，则返回 NULL
  • 结论
    让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环
    运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。
  • 证明
    在这里插入图片描述
  1. 给定一个链表，每个结点包含一个额外增加的随机指针，该指针可以指向链表中的任何结点
    或空结点。
    要求返回这个链表的深度拷贝
  2. 其他 。ps：链表的题当前因为难度及知识面等等原因还不适合我们当前学习，大家可以先把c++学一下，在逐步开始刷题 Leetcode + 牛客

1.5 双向链表的实现

// 2、带头+双向+循环链表增删查改实现
typedef int LTDataType;
typedef struct ListNode
{
 LTDataType _data;
 struct ListNode* next;
 struct ListNode* prev;
}ListNode;
// 创建返回链表的头结点.
ListNode* ListCreate();
// 双向链表销毁
void ListDestory(ListNode* plist);
// 双向链表打印
void ListPrint(ListNode* plist);
// 双向链表尾插
void ListPushBack(ListNode* plist, LTDataType x);
// 双向链表尾删
void ListPopBack(ListNode* plist);
// 双向链表头插
void ListPushFront(ListNode* plist, LTDataType x);
// 双向链表头删
void ListPopFront(ListNode* plist);
// 双向链表查找
ListNode* ListFind(ListNode* plist, LTDataType x);
// 双向链表在pos的前面进行插入
void ListInsert(ListNode* pos, LTDataType x);
// 双向链表删除pos位置的结点
void ListErase(ListNode* pos);

二、顺序表和链表的区别

不同点顺序表链表
存储空间上物理上一定连续逻辑上连续，但物理上不一定连续
随机访问支持O(1)不支持：O(N)
任意位置插入或者删除元素可能需要搬移元素，效率低O(N)只需修改指针指向
插入动态顺序表，空间不够时需要扩容没有容量的概念
应用场景元素高效存储+频繁访问任意位置插入和删除频繁
缓存利用率高低

备注：缓存利用率参考存储体系结构 以及 局部原理性。

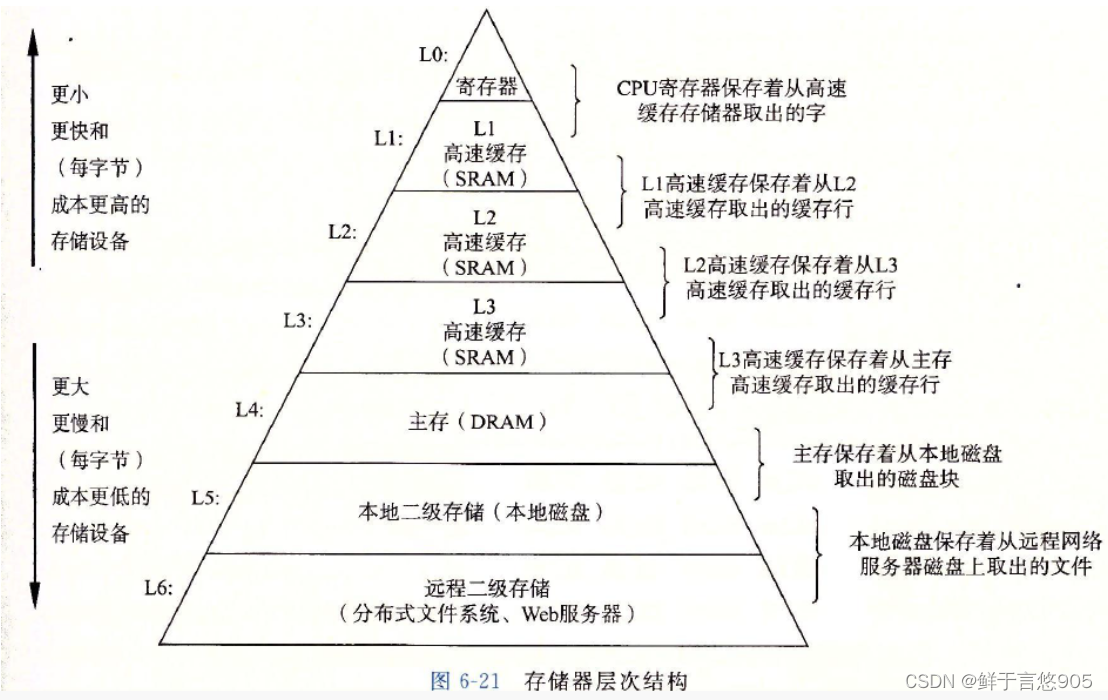
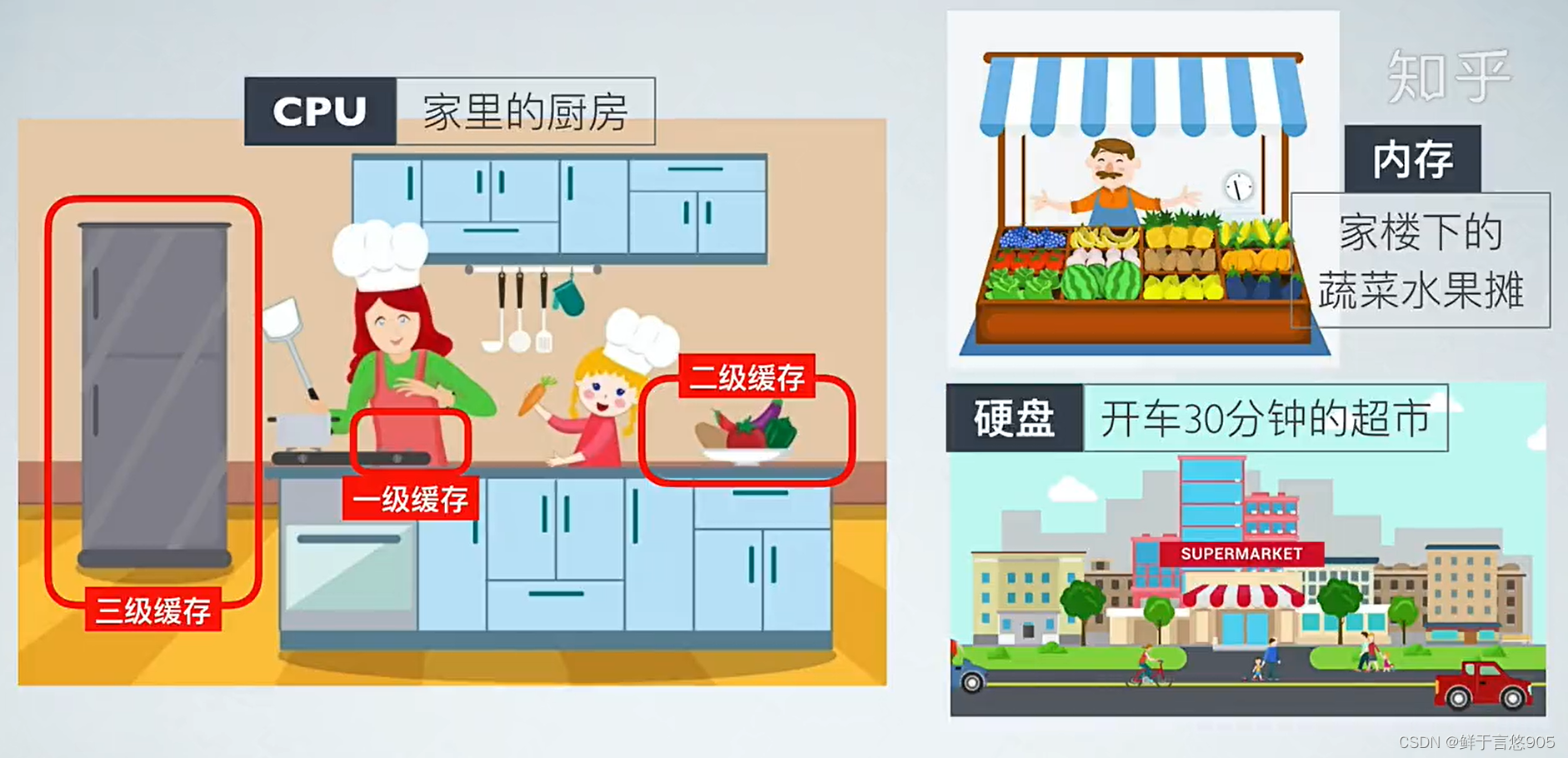
在这里插入图片描述
在这里插入图片描述

与程序员相关的CPU缓存知识

三、单项链表实现具体代码

text.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int SLTDataType;

typedef struct SListNode
{
	SLTDataType data;
	struct SListNode* next;
}SLTNode,*Node;

void SLTPrint(Node phead);
Node SLTBuyNode(SLTDataType x);//开辟空间
//链表的头插、尾插
void SLTPushBack(Node* pphead, SLTDataType x);
void SLTPushFront(Node* pphead, SLTDataType x);

//链表的头删、尾删
void SLTPopBack(Node* pphead);//尾删
void SLTPopFront(Node* pphead);//头删

//查找
Node SLTFind(Node* pphead, SLTDataType x);

//在指定位置之前插入数据
void SLTInsert(Node*  pphead, Node pos, SLTDataType x);
//在指定位置之后插入数据
void SLTInsertAfter(Node pos, SLTDataType x);

//删除pos节点
void SLTErase(Node* pphead, Node pos);
//删除pos之后的节点
void SLTEraseAfter(Node pos);

//销毁链表
void SListDesTroy(Node* pphead);

text.c

#include "text.h"
void SLTPrint(Node phead)
{
	assert(phead);
	Node purt = phead;
	while (purt)
	{
		printf("%d->", purt->data);
		purt = purt->next;
	}
	printf("NULL\n");
}
Node SLTBuyNode(SLTDataType x)
{
	Node str = (Node)malloc(sizeof(SLTNode));
	assert(str);
	str->data = x;
	str->next = NULL;
	return str;
}
void SLTPushBack(Node* pphead, SLTDataType x)
{
	assert(pphead);
	Node newnode = SLTBuyNode(x);
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	else
	{
		Node ptail = *pphead;
		while (ptail->next)
		{
			ptail = ptail->next;
		}
		ptail->next = newnode;
	}
}
void SLTPushFront(Node* pphead, SLTDataType x)
{
	assert(pphead);
	Node newnode = SLTBuyNode(x);
	newnode->next = *pphead;
	*pphead = newnode;
}
void SLTPopBack(Node* pphead)
{
	assert(pphead);
	assert(*pphead);
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	Node ptail = *pphead;
	while (ptail->next->next)
	{
		ptail = ptail->next;
	}
	free(ptail->next);
	ptail->next= NULL;
}
void SLTPopFront(Node* pphead)
{
	assert(pphead);
	assert(*pphead);
	Node next = (*pphead)->next;
	free(*pphead);
	(*pphead) = next;
}
Node SLTFind(Node* pphead, SLTDataType x)
{
	assert(pphead);
	assert(*pphead);
	Node next = *pphead;
	while (next)
	{
		if (next->data == x)
		{
			printf("找到了\n");
			return next;
		}
		next = next->next;
	}
	return NULL;
}
void SLTInsert(Node* pphead, Node pos, SLTDataType x) {
	assert(pphead);
	assert(pos);
	//要加上链表不能为空
	assert(*pphead);

	Node newnode = SLTBuyNode(x);
	//pos刚好是头结点
	if (pos == *pphead) {
		//头插
		SLTPushFront(pphead, x);
		return;
	}

	//pos不是头结点的情况
	Node prev = *pphead;
	while (prev->next != pos)
	{
		prev = prev->next;
	}
	//prev -> newnode -> pos
	prev->next = newnode;
	newnode->next = pos;
}
void SLTInsertAfter(Node pos, SLTDataType x)
{
	assert(pos);
	Node newnode = SLTBuyNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}
void SLTErase(Node* pphead, Node pos)
{
	assert(pphead);
	assert(*pphead);
	assert(pos);
	Node node = *pphead;
	if (pos == *pphead)
	{
		SLTPopFront(&pos);
	}
	while (node->next != pos)
	{
		node = node->next;
	}
	node->next = pos->next;
	free(pos);
	pos = NULL;
}
void SLTEraseAfter(Node pos)
{
	assert(pos);
	assert(pos->next);
	Node next = pos->next,pre;
	while (next)
	{
		pre = next->next;
		free(next);
		next = pre;
	}
	pos->next = NULL;
}
void SListDesTroy(Node* pphead) {
	assert(pphead);
	assert(*pphead);
	Node pcur = *pphead;
	while (pcur)
	{
		Node next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}

main.c

#include"text.h"

void SlistTest01() {
	//一般不会这样去创建链表，这里只是为了给大家展示链表的打印
	SLTNode* node1 = (SLTNode*)malloc(sizeof(SLTNode));
	node1->data = 1;
	SLTNode* node2 = (SLTNode*)malloc(sizeof(SLTNode));
	node2->data = 2;
	SLTNode* node3 = (SLTNode*)malloc(sizeof(SLTNode));
	node3->data = 3;
	SLTNode* node4 = (SLTNode*)malloc(sizeof(SLTNode));
	node4->data = 4;

	node1->next = node2;
	node2->next = node3;
	node3->next = node4;
	node4->next = NULL;

	SLTNode* plist = node1;
	SLTPrint(plist);
}
void SlistTest02() {
	Node plist = NULL;
	SLTPushBack(&plist, 1);
	SLTPushBack(&plist, 2);
	SLTPushBack(&plist, 3);
	SLTPushBack(&plist, 4);
	SLTPrint(plist); //1->2->3->4->NULL

	SLTPushFront(&plist, 5);
	SLTPrint(plist);          //5->1->2->3->4->NULL
	SLTPushFront(&plist, 6);
	SLTPrint(plist);         //6->5->1->2->3->4->NULL
	SLTPushFront(&plist, 7);
	SLTPrint(plist);         //7-6->5->1->2->3->4->NULL

	SLTPopBack(&plist);
	SLTPrint(plist);//1->2->3->NULL
	SLTPopBack(&plist);
	SLTPrint(plist);//1->2->3->NULL
	SLTPopBack(&plist);
	SLTPrint(plist);//1->2->3->NULL
	SLTPopBack(&plist);
	SLTPrint(plist);//1->2->3->NULL
	SLTPopBack(&plist);
	SLTPrint(plist);//1->2->3->NULL
}

void SlistTest03() {
	Node plist = NULL;
	SLTPushBack(&plist, 1);
	SLTPushBack(&plist, 2);
	SLTPushBack(&plist, 3);
	SLTPushBack(&plist, 4);
	SLTPrint(plist); //1->2->3->4->NULL

	/*SListDesTroy(&plist);*/
	//头删
	SLTPopFront(&plist);
	SLTPrint(plist);    //2->3->4->NULL
	SLTPopFront(&plist);
	SLTPrint(plist);    //3->4->NULL
	SLTPopFront(&plist);
	SLTPrint(plist);    //4->NULL
	//SLTPopFront(&plist);
	//SLTPrint(plist);    //NULL
	SLTPopFront(&plist);
	SLTPrint(plist);    //assert
	
	SLTNode* FindRet = SLTFind(&plist, 3);
	if (FindRet) {
		printf("找到了！\n");
	}
	else {
		printf("未找到！\n");
	}
	//SLTInsert(&plist, FindRet, 100);
	//SLTInsertAfter(FindRet, 100);
	//
	删除指定位置的节点
	//SLTErase(&plist, FindRet);
	//SLTPrint(plist); //1->2->3->NULL
}
int main() {
	//SlistTest01();
	/*SlistTest02();*/
	SlistTest03();
	return 0;
}

单链表的打印

void SLTPrint(Node phead)

void SLTPrint(Node phead)
{
	assert(phead);
	Node purt = phead;
	while (purt)
	{
		printf("%d->", purt->data);
		purt = purt->next;
	}
	printf("NULL\n");
}

单链表的打印是链表操作中的一个基础且重要的环节。链表是一种常见的数据结构，它由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针。而单链表则是链表的一种，它的特点是每个节点只包含一个指向下一个节点的指针。

在打印单链表时，我们通常需要遍历整个链表，依次访问每个节点，并输出节点的数据部分。这个过程可以通过设置一个指针，初始时指向链表的头节点，然后不断将指针移动到下一个节点，直到指针为空，即遍历完整个链表。

为了实现单链表的打印，我们可以定义一个函数，该函数接受链表的头节点作为参数。在函数内部，我们使用一个循环来遍历链表。在每次循环中，我们输出当前节点的数据部分，并将指针移动到下一个节点。当指针为空时，循环结束，打印操作完成。

空间的开辟

Node SLTBuyNode(SLTDataType x);//开辟空间

Node SLTBuyNode(SLTDataType x)
{
	Node str = (Node)malloc(sizeof(SLTNode));
	assert(str);
	str->data = x;
	str->next = NULL;
	return str;
}

链表的头插、尾插

//链表的头插、尾插
void SLTPushBack(Node* pphead, SLTDataType x);
void SLTPushFront(Node* pphead, SLTDataType x);

void SLTPushBack(Node* pphead, SLTDataType x)
{
	assert(pphead);
	Node newnode = SLTBuyNode(x);
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	else
	{
		Node ptail = *pphead;
		while (ptail->next)
		{
			ptail = ptail->next;
		}
		ptail->next = newnode;
	}
}
void SLTPushFront(Node* pphead, SLTDataType x)
{
	assert(pphead);
	Node newnode = SLTBuyNode(x);
	newnode->next = *pphead;
	*pphead = newnode;
}

链表的头插、尾插是链表操作中常见的两种插入方式，它们在处理链表数据结构时各有特点，也适用于不同的应用场景。

头插法，顾名思义，是在链表的头部插入新的节点。这种操作的时间复杂度通常为O(1)，因为无论链表长度如何，只需要修改头指针和新节点的指针即可。头插法的优点是插入速度快，但缺点是在某些情况下可能导致链表变得不均衡，特别是在大量连续的头插操作中，链表可能会退化成类似栈的结构，影响后续操作的效率。

尾插法则是在链表的尾部插入新的节点。这种操作的时间复杂度通常为O(n)，因为需要遍历链表找到尾节点。尾插法的优点是能保持链表的相对均衡，减少链表操作中的性能瓶颈。然而，它的缺点是在大量连续的尾插操作中，需要不断遍历链表，相对头插法来说效率较低。

在实际应用中，选择头插还是尾插，需要根据具体的需求和场景来决定。例如，在实现一个基于链表的栈时，头插法是一个很好的选择，因为栈的特性就是后进先出（LIFO），头插法能很好地满足这一需求。而在实现一个基于链表的队列时，尾插法则更为合适，因为队列的特性是先进先出（FIFO），尾插法能保持链表的顺序性，使得出队操作更加高效。

此外，在实际编程中，还需要注意链表操作的边界条件和特殊情况，如空链表的处理、内存分配失败的处理等。

链表的头删、尾删

//链表的头删、尾删
void SLTPopBack(Node* pphead);//尾删
void SLTPopFront(Node* pphead);//头删

void SLTPopBack(Node* pphead)
{
	assert(pphead);
	assert(*pphead);
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	Node ptail = *pphead;
	while (ptail->next->next)
	{
		ptail = ptail->next;
	}
	free(ptail->next);
	ptail->next= NULL;
}
void SLTPopFront(Node* pphead)
{
	assert(pphead);
	assert(*pphead);
	Node next = (*pphead)->next;
	free(*pphead);
	(*pphead) = next;
}

链表的头删、尾删是链表操作中的基础内容，对于理解链表结构和实现链表功能至关重要。在链表中，头删指的是删除链表中的第一个元素，而尾删则是删除链表中的最后一个元素。这个过程中，需要注意更新头节点的指针，并确保原头节点在删除后能够被正确释放，以避免内存泄漏。

相比之下，尾删操作稍微复杂一些。因为需要找到链表的最后一个节点，并将其前一个节点的指针设置为null。同样，在删除尾节点之前，也需要判断链表是否为空。如果链表只有一个节点，那么头删和尾删是等价的。如果链表有多个节点，则需要遍历链表，找到最后一个节点，并执行删除操作。

除了基本的头删和尾删操作，链表还支持在中间位置插入和删除节点。这些操作同样需要对链表结构有深入的理解，并且能够正确处理各种边界情况。在实际应用中，链表的操作通常与其他数据结构或算法相结合，以实现更复杂的功能。通过熟练掌握链表操作，可以更好地理解和应用链表这一基础数据结构。

链表中元素的查找

//查找
Node SLTFind(Node* pphead, SLTDataType x);

Node SLTFind(Node* pphead, SLTDataType x)
{
	assert(pphead);
	assert(*pphead);
	Node next = *pphead;
	while (next)
	{
		if (next->data == x)
		{
			printf("找到了\n");
			return next;
		}
		next = next->next;
	}
	return NULL;
}

链表中元素的查找是数据结构和算法中的一个基础问题。在链表中查找元素，不同于在数组中的直接索引访问，它通常需要从链表的头部或尾部开始，逐个节点地遍历，直到找到目标元素或者遍历完整个链表。这种查找方式的时间复杂度通常是O(n)，其中n是链表的长度。

链表的查找性能可以通过一些优化手段来提升。例如，如果链表是有序的，那么可以使用二分查找等更高效的算法来减少查找时间。然而，这种优化通常要求链表在插入和删除元素时保持有序状态，这会增加这些操作的复杂度。

在实现链表查找时，我们通常会使用一个循环来遍历链表。在每次迭代中，我们将当前节点的值与目标值进行比较。如果找到匹配的值，则返回当前节点的位置或引用；如果遍历完整个链表都没有找到匹配的值，则返回null或表示未找到的特殊值。

链表在指定位置之前、之后插入数据

//在指定位置之前插入数据
void SLTInsert(Node*  pphead, Node pos, SLTDataType x);
//在指定位置之后插入数据
void SLTInsertAfter(Node pos, SLTDataType x);

void SLTInsert(Node* pphead, Node pos, SLTDataType x) {
	assert(pphead);
	assert(pos);
	//要加上链表不能为空
	assert(*pphead);

	Node newnode = SLTBuyNode(x);
	//pos刚好是头结点
	if (pos == *pphead) {
		//头插
		SLTPushFront(pphead, x);
		return;
	}

	//pos不是头结点的情况
	Node prev = *pphead;
	while (prev->next != pos)
	{
		prev = prev->next;
	}
	//prev -> newnode -> pos
	prev->next = newnode;
	newnode->next = pos;
}
void SLTInsertAfter(Node pos, SLTDataType x)
{
	assert(pos);
	Node newnode = SLTBuyNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}

链表在指定位置之前、之后插入数据是链表操作中的基本功能。链表作为一种常见的数据结构，由一系列节点组成，每个节点包含数据和指向下一个节点的指针。这种结构允许我们在不移动其他元素的情况下插入或删除元素，因此在许多场景中都非常有用。

首先，我们要明确链表的基本结构。通常，链表节点包含一个数据域和一个指针域。数据域用于存储实际的数据，而指针域则用于指向链表中的下一个节点。对于头节点，其指针域指向链表的第一个节点；对于尾节点，其指针域通常指向空（NULL），表示链表的结束。

在链表中插入数据之前，我们需要确定插入的位置。这可以通过使用索引或遍历链表直到找到适当的节点来实现。一旦找到插入位置，我们就可以创建一个新的节点，并将其插入到链表中。

要在指定位置之后插入数据，我们需要找到该位置的前一个节点。然后，我们将新节点的指针域设置为当前节点的指针域所指向的节点，同时将当前节点的指针域设置为新节点。这样，新节点就被插入到了指定位置之后。

要在指定位置之前插入数据，我们需要找到该位置的节点。然后，我们将新节点的指针域设置为当前节点，并将当前节点的前一个节点的指针域设置为新节点。这样，新节点就被插入到了指定位置之前。

需要注意的是，在插入节点时，我们必须确保正确地更新指针域，以保持链表的完整性和正确性。此外，我们还需要考虑链表的边界情况，例如在链表头部或尾部插入节点时。

在插入数据后，链表的结构可能会发生变化，因此任何依赖于链表结构的操作都可能需要重新评估或调整。此外，插入操作可能会增加链表的长度，这可能会影响链表的性能，特别是在进行搜索或遍历操作时。

总的来说，链表在指定位置之前或之后插入数据是链表操作中的基本操作之一。通过正确地实现这些操作，我们可以充分利用链表的优势，高效地管理和操作数据。

删除链表中的结点

//删除pos节点
void SLTErase(Node* pphead, Node pos);
//删除pos之后的节点
void SLTEraseAfter(Node pos);

void SLTErase(Node* pphead, Node pos)
{
	assert(pphead);
	assert(*pphead);
	assert(pos);
	Node node = *pphead;
	if (pos == *pphead)
	{
		SLTPopFront(&pos);
	}
	while (node->next != pos)
	{
		node = node->next;
	}
	node->next = pos->next;
	free(pos);
	pos = NULL;
}
void SLTEraseAfter(Node pos)
{
	assert(pos);
	assert(pos->next);
	Node next = pos->next,pre;
	while (next)
	{
		pre = next->next;
		free(next);
		next = pre;
	}
	pos->next = NULL;
}

删除链表中的结点是一项常见的编程任务，它要求我们在保持链表其他部分完整的同时，移除指定的结点。链表是一种常见的数据结构，它由一系列节点组成，每个节点都包含数据部分和指向下一个节点的指针。为了有效地删除链表中的某个节点，我们需要遵循一定的步骤，并确保不会破坏链表的完整性。

首先，我们需要确定要删除的节点。这通常是通过节点的值或者节点在链表中的位置来实现的。在知道要删除的节点之后，我们需要考虑几种不同的删除情况：

如果要删除的节点是链表的第一个节点，我们需要更新链表的头指针，使其指向第二个节点。

如果要删除的节点是链表的最后一个节点，我们需要找到倒数第二个节点，并将其指针部分设置为null，从而切断与最后一个节点的连接。

如果要删除的节点位于链表的中间，我们需要找到该节点的前一个节点，并将其指针部分更新为指向要删除节点的下一个节点，从而跳过要删除的节点。

在删除节点的过程中，我们必须确保正确地处理内存，以防止内存泄漏。这通常意味着在删除节点后，我们需要释放该节点所占用的内存。

销毁链表

//销毁链表
void SListDesTroy(Node* pphead);

void SListDesTroy(Node* pphead) {
	assert(pphead);
	assert(*pphead);
	Node pcur = *pphead;
	while (pcur)
	{
		Node next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}

链表，这种数据结构在计算机科学中占据着举足轻重的地位，其通过节点之间的链接来存储数据，每个节点都包含数据和指向下一个节点的指针。然而，当链表不再需要时，如何正确地销毁它，释放其占用的内存，就显得尤为重要。

销毁链表的过程通常包括两个主要步骤：遍历链表和释放内存。首先，我们需要从链表的头节点开始，逐个访问链表中的每个节点。在访问每个节点时，我们需要记录下一个节点的位置，以便在释放当前节点后能够继续遍历链表。同时，我们还需要注意处理链表的尾节点，确保不会出现内存泄漏。

在遍历链表的过程中，我们可以通过修改指针的指向来逐个断开节点之间的链接。具体来说，我们可以将当前节点的下一个节点的指针置为null，这样当前节点就不再指向下一个节点，从而实现了断开链接的目的。然后，我们可以释放当前节点所占用的内存，通常可以使用操作系统提供的内存释放函数来完成这一操作。

在释放内存时，我们需要格外小心。一方面，我们需要确保只释放链表节点所占用的内存，而不要误释放其他重要数据的内存。另一方面，我们还需要注意处理可能出现的异常情况，例如内存释放失败等。为了避免这些问题，我们可以使用智能指针等高级内存管理技术来辅助销毁链表。

总的来说，销毁链表是一个复杂而重要的任务。我们需要仔细遍历链表中的每个节点，逐个断开链接并释放内存，以确保链表能够被正确地销毁。同时，我们还需要注意处理可能出现的异常情况，保证程序的稳定性和可靠性。只有这样，我们才能在享受链表带来的便利的同时，避免其带来的潜在风险。

四、双向循环链表代码的具体实现

text.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include<assert.h>

//定义双向链表中节点的结构
typedef int LTDataType;
typedef struct ListNode {
	LTDataType data;
	struct ListNode* prev;
	struct ListNode* next;
}LTNode,* Node;

//注意，双向链表是带有哨兵位的，插入数据之前链表中必须要先初始化一个哨兵位
//void LTInit(Node* pphead);
Node LTInit();
Node LTBuyNode(LTDataType x);
//void LTDesTroy(Node* pphead);
void LTDesTroy(Node phead);   //推荐一级（保持接口一致性）

void LTPrint(Node phead);

//不需要改变哨兵位，则不需要传二级指针
//如果需要修改哨兵位的话，则传二级指针
void LTPushBack(Node phead, LTDataType x);
void LTPushFront(Node phead, LTDataType x);

//头删、尾删
void LTPopBack(Node phead);
void LTPopFront(Node phead);

//查找
Node LTFind(Node phead, LTDataType x);

//在pos位置之后插入数据
void LTInsert(Node pos, LTDataType x);
//删除pos位置的数据
void LTErase(Node pos);

text.c

#include "text.h"
Node LTBuyNode(LTDataType x)
{
	Node phead = (Node)malloc(sizeof(LTNode));
	assert(phead);
	phead->data = x;
	phead->prev = phead;
	phead->next = phead;
	return phead;
}
Node LTInit()
{
	Node phead = LTBuyNode(-1);
	return phead;
}
void LTDesTroy(Node phead)
{
	assert(phead);
	/*Node ret;
	while (phead->next != phead)
	{
		ret = phead->next;
		phead->next = ret->next;
		phead->next->prev = phead;
		free(ret);
	}
	free(phead);
	phead = NULL;*/
	Node pur = phead->next;
	while (pur != phead)
	{
		Node next = pur->next;
		free(pur);
		pur = next;
	}
	free(phead);
	phead = NULL;
}
void LTPrint(Node phead)
{
	assert(phead);
	Node pur = phead->next;
	while (pur!= phead)
	{
		printf("%d->", pur->data);
		pur = pur->next;
	}
	printf("NULL\n");
}
void LTPushBack(Node phead, LTDataType x)
{
	assert(phead);
	Node newnode = LTBuyNode(x);
	phead->prev->next = newnode;
	newnode->prev = phead->prev;
	newnode->next = phead;
	phead->prev = newnode;
}
void LTPushFront(Node phead, LTDataType x)
{
	assert(phead);
	Node newnode = LTBuyNode(x);
	newnode->next = phead->next;
	phead->next->prev = newnode;
	newnode->prev = phead;
	phead->next = newnode;
}
void LTPopBack(Node phead)
{
	assert(phead);
	assert(phead->next != phead);
	Node pur = phead->prev;
	pur->prev->next = phead;
	phead->prev = pur->prev;
	free(pur);
	pur = NULL;
}
void LTPopFront(Node phead)
{
	assert(phead);
	assert(phead->next != phead);
	Node pur = phead->next;
	phead->next = pur->next;
	pur->next->prev = phead;
	free(pur);
	pur = NULL;
}

Node LTFind(Node phead, LTDataType x)
{
	assert(phead);
	Node pur = phead->next;
	while (pur != phead)
	{
		if (pur->data == x)return pur;
		pur = pur->next;
	}
	return NULL;
}
void LTInsert(Node pos, LTDataType x) {
	assert(pos);
	Node newnode = LTBuyNode(x);
	//pos newnode pos->next
	newnode->next = pos->next;
	newnode->prev = pos;

	pos->next->prev = newnode;
	pos->next = newnode;
}
//删除pos位置的数据
void LTErase(Node pos) {
	assert(pos);

	//pos->prev pos  pos->next
	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;

	free(pos);
	pos = NULL;
}

main.c

#include "text.h"
void ListTest01() {
	//LTNode* plist = NULL;
	//LTInit(&plist);

	Node plist = LTInit();
	//尾插
	/*LTPushBack(plist, 1);
	LTPushBack(plist, 2);
	LTPushBack(plist, 3);
	LTPushBack(plist, 4);
	LTPrint(plist);*/
	//头插
	LTPushFront(plist, 1);
	LTPushFront(plist, 2);
	LTPushFront(plist, 3);
	LTPushFront(plist, 4);
	LTPrint(plist);       //4->3->2->1->

	//
	/*LTPopBack(plist);
	LTPrint(plist);
	LTPopBack(plist);
	LTPrint(plist);
	LTPopBack(plist);
	LTPrint(plist);
	LTPopBack(plist);
	LTPrint(plist);
	LTPopBack(plist);*/
	//LTPrint(plist);
	//
	//头删
	/*LTPopFront(plist);
	LTPrint(plist);
	LTPopFront(plist);
	LTPrint(plist);
	LTPopFront(plist);
	LTPrint(plist);
	LTPopFront(plist);
	LTPrint(plist);
	LTPopFront(plist);*/
	//LTPrint(plist);

	Node findRet = LTFind(plist, 3);
	if (findRet == NULL) {
		printf("未找到！\n");
	}
	else {
		printf("找到了！\n");
	}
	在指定位置之后插入数据
	LTInsert(findRet, 66); //4->3->2->1->66->
	LTPrint(plist);

	//删除pos位置的节点
	LTErase(findRet);
	LTPrint(plist);
	LTDesTroy(plist);
	plist = NULL;
}

int main() {
	ListTest01();
	return 0;
}

双向循环链表的创建

Node LTBuyNode(LTDataType x);

Node LTBuyNode(LTDataType x)
{
	Node phead = (Node)malloc(sizeof(LTNode));
	assert(phead);
	phead->data = x;
	phead->prev = phead;
	phead->next = phead;
	return phead;
}

双向循环链表的初始化

Node LTInit();

Node LTInit()
{
	Node phead = LTBuyNode(-1);
	return phead;
}

在开始编写双向循环链表的初始化代码之前，我们首先需要理解双向循环链表的基本结构。双向循环链表是一种线性数据结构，它包含了一个指向前一个节点的“前指针”和一个指向下一个节点的“后指针”。与传统的双向链表不同，双向循环链表的最后一个节点的后指针指向第一个节点，而第一个节点的前指针则指向最后一个节点，从而形成一个闭环。

双向循环链表的销毁

void LTDesTroy(Node phead);   //推荐一级（保持接口一致性）

void LTDesTroy(Node phead)
{
	assert(phead);
	/*Node ret;
	while (phead->next != phead)
	{
		ret = phead->next;
		phead->next = ret->next;
		phead->next->prev = phead;
		free(ret);
	}
	free(phead);
	phead = NULL;*/
	Node pur = phead->next;
	while (pur != phead)
	{
		Node next = pur->next;
		free(pur);
		pur = next;
	}
	free(phead);
	phead = NULL;
}

接口一致性
可以这样理解，就想象你现在是用户，你是想在使用这个软件的时候操作简单还是操作困难，按照正常人来说，肯定是越简单越好，这时候就需要接口一致了，我们作为这个软件的设计者，我们需要把这个软件做的越简单越好

在数据结构和算法的世界里，双向循环链表是一种独特而高效的数据结构。它允许我们在任意节点向前或向后移动，从而方便地访问链表中的任何元素。然而，就像所有资源一样，当我们不再需要双向循环链表时，必须妥善地销毁它，以防止内存泄漏和其他潜在问题。

销毁双向循环链表的过程涉及几个关键步骤。首先，我们必须遍历链表，释放每个节点所占用的内存。由于双向循环链表的特性，我们可以从任何一个节点开始遍历。为了简化操作，我们通常选择头节点作为起点。

在遍历过程中，我们需要逐个访问链表中的每个节点，并释放其内存。这通常通过调用适当的内存释放函数来完成，例如在C++中使用delete操作符，或在C语言中使用free函数。在释放节点内存之前，我们还需确保已经断开了该节点与前一个节点和后一个节点的连接，以防止出现悬挂指针。

一旦所有节点的内存都被释放，我们就需要检查链表的头指针是否已经被正确设置为null或nullptr。这是为了确保链表已经被完全销毁，并且任何尝试访问它的操作都会失败。

值得注意的是，双向循环链表的销毁过程必须小心谨慎，以确保没有遗漏任何节点。否则，未被释放的内存可能会导致内存泄漏，进而影响程序的性能和稳定性。

综上所述，双向循环链表的销毁是一个重要而必要的操作。通过正确地释放每个节点的内存，并断开它们之间的连接，我们可以确保链表被完全销毁，从而避免潜在的内存泄漏和其他问题。这种负责任的资源管理实践是编写高效、可靠的代码的重要组成部分。

双向循环链表的打印

void LTPrint(Node phead);

void LTPrint(Node phead)
{
	assert(phead);
	Node pur = phead->next;
	while (pur!= phead)
	{
		printf("%d->", pur->data);
		pur = pur->next;
	}
	printf("NULL\n");
}

双向循环链表的头插和尾插

//不需要改变哨兵位，则不需要传二级指针
//如果需要修改哨兵位的话，则传二级指针
void LTPushBack(Node phead, LTDataType x);
void LTPushFront(Node phead, LTDataType x);

void LTPushBack(Node phead, LTDataType x)
{
	assert(phead);
	Node newnode = LTBuyNode(x);
	phead->prev->next = newnode;
	newnode->prev = phead->prev;
	newnode->next = phead;
	phead->prev = newnode;
}
void LTPushFront(Node phead, LTDataType x)
{
	assert(phead);
	Node newnode = LTBuyNode(x);
	newnode->next = phead->next;
	phead->next->prev = newnode;
	newnode->prev = phead;
	phead->next = newnode;
}

双向循环链表的头删和尾删

//头删、尾删
void LTPopBack(Node phead);
void LTPopFront(Node phead);

void LTPopBack(Node phead)
{
	assert(phead);
	assert(phead->next != phead);
	Node pur = phead->prev;
	pur->prev->next = phead;
	phead->prev = pur->prev;
	free(pur);
	pur = NULL;
}
void LTPopFront(Node phead)
{
	assert(phead);
	assert(phead->next != phead);
	Node pur = phead->next;
	phead->next = pur->next;
	pur->next->prev = phead;
	free(pur);
	pur = NULL;
}

双向循环链表的元素查找

//查找
Node LTFind(Node phead, LTDataType x);

Node LTFind(Node phead, LTDataType x)
{
	assert(phead);
	Node pur = phead->next;
	while (pur != phead)
	{
		if (pur->data == x)return pur;
		pur = pur->next;
	}
	return NULL;
}

双向循环链表的插入和删除

//在pos位置之后插入数据
void LTInsert(Node pos, LTDataType x);
//删除pos位置的数据
void LTErase(Node pos);

void LTInsert(Node pos, LTDataType x) {
	assert(pos);
	Node newnode = LTBuyNode(x);
	//pos newnode pos->next
	newnode->next = pos->next;
	newnode->prev = pos;

	pos->next->prev = newnode;
	pos->next = newnode;
}
//删除pos位置的数据
void LTErase(Node pos) {
	assert(pos);

	//pos->prev pos  pos->next
	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;

	free(pos);
	pos = NULL;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1488817.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【C++基础】STL容器面试题分享||上篇

【C++基础】STL容器面试题分享||上篇

&#x1f308;欢迎来到C基础专栏 &#x1f64b;&#x1f3fe;‍♀️作者介绍&#xff1a;前PLA队员 目前是一名普通本科大三的软件工程专业学生 &#x1f30f;IP坐标&#xff1a;湖北武汉 &#x1f349; 目前技术栈&#xff1a;C/C STL 1.请说说 STL 的基本组成部分2.详细的说&…
阅读更多...
SwiftUI 在 App 中弹出全局消息横幅（下）

SwiftUI 在 App 中弹出全局消息横幅（下）

功能需求 在 SwiftUI 开发的 App 界面中，有时我们需要在全局层面向用户展示一些消息： 如上图所示：我们弹出的全局消息横幅位于所有视图之上，这意味这它不会被任何东西所遮挡；而且用户可以点击该横幅关闭它。这是怎么做到的呢？ 在本篇博文中，您将学到以下内容 功能需求…
阅读更多...
C++/WinRT教程（第三篇）API的使用

C++/WinRT教程（第三篇）API的使用

目录 前言 Windows API 在WinRT中的投影 C/WinRT的头文件&#xff08;投影标头&#xff09; 通过对象、接口或通过 ABI 访问成员 投影类型的初始化方法 不要错误地使用延迟初始化 不要错误地使用复制构造 使用 winrt::make 进行构造 标准构造方法 在WinRT组件中实现A…
阅读更多...
Linux--文件(2)-重定向和文件缓冲

Linux--文件(2)-重定向和文件缓冲

命令行中的重定向符号 介绍和使用 在Linux的命令行中&#xff0c;重定向符号用于将命令的输入或输出重定向到文件或设备。 常见的重定向符号&#xff1a; 1.“>“符号&#xff1a;将命令的标准输出重定向到指定文件中&#xff0c;并覆盖原有的内容。 2.”>>“符号&a…
阅读更多...
C/C++工程师面试题（STL篇）

C/C++工程师面试题（STL篇）

STL 中有哪些常见的容器 STL 中容器分为顺序容器、关联式容器、容器适配器三种类型&#xff0c;三种类型容器特性分别如下&#xff1a; 1. 顺序容器 容器并非排序的&#xff0c;元素的插入位置同元素的值无关&#xff0c;包含 vector、deque、list vector&#xff1a;动态数组…
阅读更多...
[Unity3d] 网络开发基础【个人复习笔记/有不足之处欢迎斧正/侵删】

[Unity3d] 网络开发基础【个人复习笔记/有不足之处欢迎斧正/侵删】

TCP/IP TCP/IP协议是一 系列规则(协议)的统称&#xff0c;他们定义了消息在网络间进行传输的规则 是供已连接互联网的设备进行通信的通信规则 OSI模型只是一个基本概念,而TCP/IP协议是基于这个概念的具体实现 TCP和UDP协议 TCP:传输控制协议&#xff0c;面向连接&#xff0c…
阅读更多...
面试经典150题——简化路径

面试经典150题——简化路径

"A goal is a dream with a deadline." - Napoleon Hill 1. 题目描述 2. 题目分析与解析 2.1 思路一 这个题目开始看起来并不太容易知道该怎么写代码&#xff0c;所以不知道什么思路那就先模拟人的行为&#xff0c;比如对于如下测试用例&#xff1a; 首先 /代表根…
阅读更多...
YOLOv8姿态估计实战：训练自己的数据集

YOLOv8姿态估计实战：训练自己的数据集

课程链接&#xff1a;https://edu.csdn.net/course/detail/39355 YOLOv8 基于先前 YOLO 版本的成功&#xff0c;引入了新功能和改进&#xff0c;进一步提升性能和灵活性。YOLOv8 同时支持目标检测和姿态估计任务。 本课程以熊猫姿态估计为例&#xff0c;将手把手地教大家使用C…
阅读更多...
使用TensorRT-LLM进行生产环境的部署指南

使用TensorRT-LLM进行生产环境的部署指南

TensorRT-LLM是一个由Nvidia设计的开源框架&#xff0c;用于在生产环境中提高大型语言模型的性能。该框架是基于 TensorRT 深度学习编译框架来构建、编译并执行计算图&#xff0c;并借鉴了许多 FastTransformer 中高效的 Kernels 实现&#xff0c;并且可以利用 NCCL 完成设备之…
阅读更多...
深入理解nginx的https alpn机制

深入理解nginx的https alpn机制

目录 1. 概述2. alpn协议的简要理解2.1 ssl的握手过程2.2 通过抓包看一下alpn的细节3. nginx源码分析3.1 给ssl上下文设置alpn回调3.2 连接初始化3.3 处理alpn协议回调3.4 握手完成，启用http协议4.4 总结阅读姊妹篇：深入理解nginx的https alpn机制 1. 概述 应用层协议协商（…
阅读更多...
大地测量学课堂笔记：1、绪论

大地测量学课堂笔记：1、绪论

慕课网址&#xff1a;https://www.icourse163.org/course/WHU-1464124180?fromsearchPage&outVendorzw_mooc_pcssjg_https://www.icourse163.org/course/WHU-1464124180?fromsearchPage&outVendorzw_mooc_pcssjg_ 1. 大地测量学的定义 大地测量学是专门研究精确测量…
阅读更多...
【数据结构】复杂度详解

【数据结构】复杂度详解

目录 &#xff08;一&#xff09;算法的复杂度 &#xff08;二&#xff09;时间复杂度 &#xff08;1&#xff09;练笔解释&#xff1a; i&#xff0c;示例1 ii&#xff0c;示例2 iii&#xff0c;二分查找 iv&#xff0c;斐波那契 &#xff08;三&#xff09;空间复杂度…
阅读更多...
java中的set

java中的set

Set Set集合概述和特点 不可以存储重复元素 没有索引,不能使用普通for循环遍历 哈希值 哈希值简介 是JDK根据对象的地址或者字符串或者数字算出来的int类型的数值 如何获取哈希值 Object类中的public int hashCode()&#xff1a;返回对象的哈希码值。 哈希值的特点 同一个…
阅读更多...
【ARM Trace32(劳特巴赫) 高级篇 21 -- SystemTrace ITM 使用介绍】

【ARM Trace32(劳特巴赫) 高级篇 21 -- SystemTrace ITM 使用介绍】

文章目录 SystemTrace ITMSystemTrace ITM 常用命令Trace Data AnalysisSystemTrace ITM CoreSight ITM (Instrumentation Trace Macrocell) provides the following information: Address, data value and instruction address for selected data cyclesInterrupt event info…
阅读更多...
C++基于多设计模式下的同步异步日志系统day5

C++基于多设计模式下的同步异步日志系统day5

C基于多设计模式下的同步&异步日志系统day5 &#x1f4df;作者主页&#xff1a;慢热的陕西人 &#x1f334;专栏链接&#xff1a;C基于多设计模式下的同步&异步日志系统 &#x1f4e3;欢迎各位大佬&#x1f44d;点赞&#x1f525;关注&#x1f693;收藏&#xff0c;&am…
阅读更多...
技术总结: PPT绘图

技术总结: PPT绘图

目录 写在前面参考文档技巧总结PPT中元素的连接立方体调整厚度调整图形中的文本3D 图片调整渐变中的颜色 写在前面 能绘制好一个好看的示意图非常重要, 在科研和工作中好的示意图能精准表达出自己的想法, 减少沟通的成本, 可视化的呈现也可以加强自身对系统的理解, 时间很久后…
阅读更多...
Unity 协程（Coroutine）到底是什么？

Unity 协程（Coroutine）到底是什么？

参考链接&#xff1a;Unity 协程(Coroutine)原理与用法详解_unity coroutine-CSDN博客 为啥在Unity中一般不考虑多线程 因为在Unity中&#xff0c;只能在主线程中获取物体的组件、方法、对象&#xff0c;如果脱离这些&#xff0c;Unity的很多功能无法实现&#xff0c;那么多线程…
阅读更多...
python lambda表达式(匿名函数)

python lambda表达式(匿名函数)

lambda 表达式 在Python中&#xff0c;匿名函数&#xff08;也称为lambda函数&#xff09;是一种简洁的方式来定义小函数&#xff0c;这些函数可以在需要的地方直接定义和使用&#xff0c;而不需要使用def关键字来定义一个具有名称的函数。 lambda 函数是一种小型、匿名的、内…
阅读更多...
vue+element ui上传图片到七牛云服务器

vue+element ui上传图片到七牛云服务器

本来打算做一个全部都是前端完成的资源上传到七牛云的demo&#xff0c;但是需要获取token&#xff0c;经历了九九八十一难&#xff0c;最终还是选择放弃&#xff0c;token从后端获取&#xff08;springboot&#xff09;。如果你们有前端直接能解决的麻烦记得私我哦&#xff01;…
阅读更多...
学习网络编程No.12【传输层协议之TCP】

学习网络编程No.12【传输层协议之TCP】

引言&#xff1a; 北京时间&#xff1a;2024/2/27/14:12&#xff0c;不知过了多久终于在今天上午更新了新的文章。促使好久没有登录CSDN的我回关了几个近期关注我的人&#xff0c;然后过了没多久有人就通过二维码加了我的微信&#xff0c;他问了我一个问题&#xff0c;如何学好…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023