Problem: 74. 搜索二维矩阵
文章目录
- 题目描述
- 思路
- 复杂度
- Code
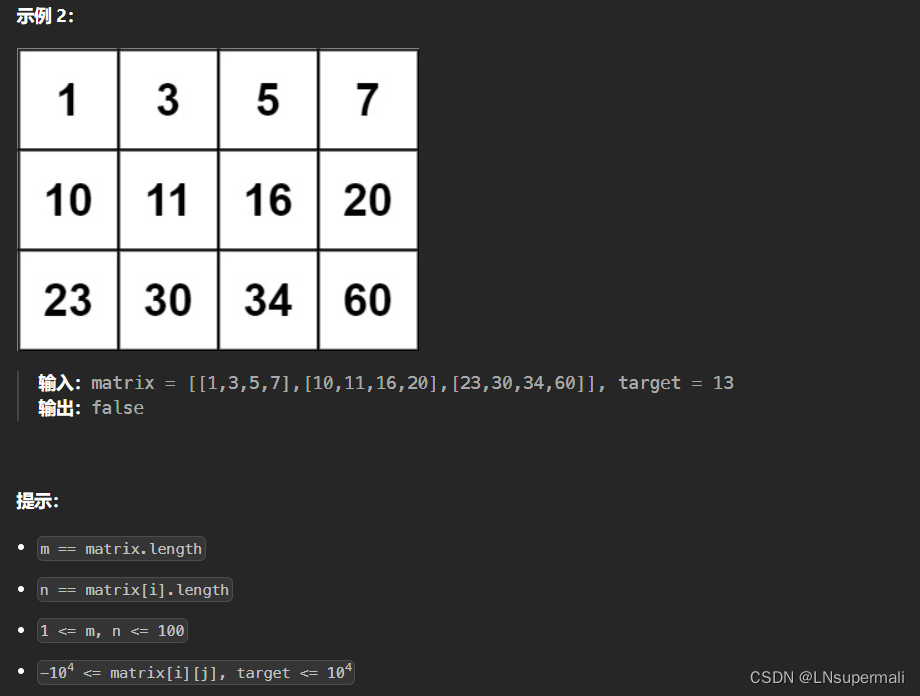
题目描述
思路
思路1:映射为一维数组二分查找
1.由于题目矩阵中的元素整体是升序的,我们可以将其放置在一个大小为 m × n m \times n m×n的一维数组array中进行二分查找
2.对应的映射关系是array[mid] == mar[mid / n][mid % n]
思路2:直接在二维矩阵上进行二分查找
1.先对二维矩阵的第一列进行二分查找,找到小于等于target的一个数,讲此行标记为rowInd
2.从rowInd开始再进行二分查找
复杂度
思路1:
时间复杂度:
O ( l o g m n ) O(logmn) O(logmn)
空间复杂度:
O ( m n ) O(mn) O(mn)
思路2:
时间复杂度:
O ( l o g m n ) O(logmn) O(logmn)
空间复杂度:
O ( 1 ) O(1) O(1)
Code
思路1:
class Solution {
public:
/**
* Binary Search
*
* @param matrix Given array
* @param target Given target number
* @return bool
*/
bool searchMatrix(vector<vector<int>> &matrix, int target) {
int row = matrix.size();
if (row == 0) {
return false;
}
int col = matrix[0].size();
int left = 0;
int right = row * col - 1;
vector<int> array(row * col);
while (left <= right) {
int mid = left + (right - left) / 2;
if (matrix[mid / col][mid % col] == target) {
return true;
} else if (matrix[mid / col][mid % col] > target) {
right = mid - 1;
} else if (matrix[mid / col][mid % col] < target) {
left = mid + 1;
}
}
return false;
}
};
思路2:
class Solution {
public:
/**
* Binary Search
*
* @param matrix Given array
* @param target Given target number
* @return bool
*/
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int row = matrix.size();
if (row == 0) {
return false;
}
int col = matrix[0].size();
int left = 0;
int right = row - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (matrix[mid][0] == target) {
return true;
} else if (matrix[mid][0] > target) {
right = mid - 1;
} else if (matrix[mid][0] < target) {
left = mid + 1;
}
}
// Check out of bounds
if (right < 0) {
return false;
}
int rowIdx = right;
left = 0;
right = col - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (matrix[rowIdx][mid] == target) {
return true;
} else if (matrix[rowIdx][mid] > target) {
right = mid - 1;
} else if (matrix[rowIdx][mid] < target) {
left = mid + 1;
}
}
return false;
}
};