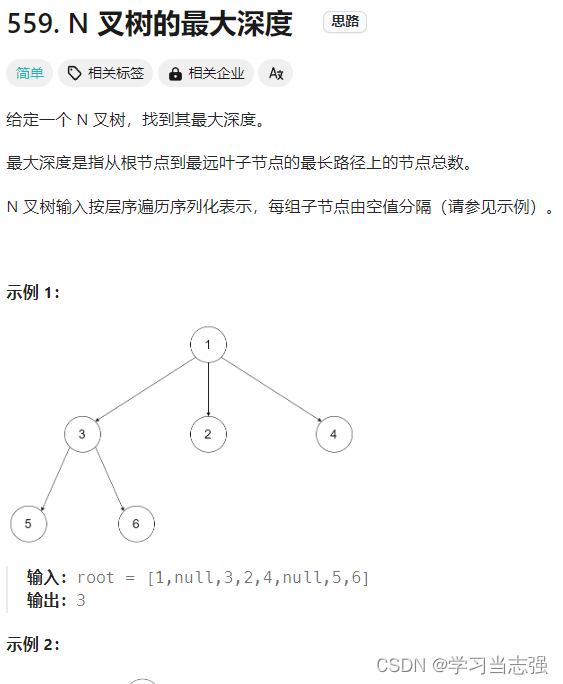
这段代码是一个Java类Solution，其中包含一个公共方法maxDepth，用于计算一个二叉树的最大深度。这里的二叉树是一个特殊的数据结构，其中每个节点Node可能有一个或多个子节点（在这里被称为children）。下面是对代码的详细注释：

// 定义一个名为Solution的类  
class Solution {  
      
    // 定义一个公共方法maxDepth，接受一个Node类型的参数root，返回int类型的结果  
    public int maxDepth(Node root) {  
        // 如果root节点为null（也就是树为空），那么树的深度为0  
        if(root==null) return 0;  
      
        // 初始化深度为0  
        int depth = 0;  
          
        // 如果root节点的子节点列表不为null  
        if(root.children != null){  
            // 遍历root节点的每一个子节点  
            for(Node children : root.children){  
                // 递归调用maxDepth方法，计算每个子节点的深度，并与当前深度比较  
                // 取两者中的最大值作为新的深度  
                depth = Math.max(depth, maxDepth(children));  
            }  
        }  
          
        // 返回当前节点的深度（即子节点的最大深度+1，1代表当前节点本身）  
        return depth + 1;  
    }  
}

这段代码的核心思想是递归。它首先检查给定的根节点是否为null，如果是，则返回深度0。然后，它遍历根节点的所有子节点，并递归地计算每个子节点的深度。最后，它返回子节点中的最大深度加1（加1是因为我们还需要考虑当前节点本身）。

注意：在这段代码中，我们假设Node类已经定义好了，并且有一个名为children的属性，它是一个Node对象的列表，表示该节点的子节点。我们还假设Node类是一个有效的二叉树节点类，其中每个节点可以有0个或多个子节点。