2023.3.3周报

摘要

一、文献阅读

1、题目

2、摘要

3、模型架构

4、文献解读

一、Introduction

二、实验

三、结论

二、PINN

一、PINN比传统数值方法有哪些优势

二、PINN方法

三、正问题与反问题

三、PINN实验

一、数学方程

二、模型搭建

总结

摘要

本周我阅读了一篇题目为Deep Residual Learning for Image Recognition的文献，文章的贡献是作者提出了残差网络的思想，且证明了更深层的残差网络具有比VGG网络更低的复杂度和更高的准确性，同时，残差网络实现了更容易的训练过程。其次，对PINN进行了继续的学习，PINN 是一种科学机器在传统数值领域的应用方法，特别是用于解决与偏微分方程相关的各种问题，包括方程求解、参数反演、模型发现、控制与优化等。

This week, I read a paper titled "Deep Residual Learning for Image Recognition." The contribution of the paper is that the author introduces the concept of residual networks and demonstrates that deeper residual networks have lower complexity and higher accuracy compared to VGG networks. Additionally, residual networks achieve a more straightforward training process. Furthermore, I gained preliminary insights into Physics-Informed Neural Networks (PINN). PINN is an application of scientific machine learning in traditional numerical domains, particularly for solving various problems related to partial differential equations. This includes equation solving, parameter inversion, model discovery, control, and optimization.

一、文献阅读

1、题目

题目：Deep Residual Learning for Image Recognition

链接：https://arxiv.org/abs/1512.03385

2、摘要

本文展示了一种残差学习框架，能够简化使那些非常深的网络的训练，该框架使得层能根据其输入来学习残差函数而非原始函数。作者提出了残差网络的思想，且证明了更深层的残差网络具有比VGG网络更低的复杂度和更高的准确性。同时，残差网络实现了更容易的训练过程。

This article presents a residual learning framework that simplifies the training of very deep networks. The framework allows layers to learn residual functions based on their inputs rather than the original functions. The author introduces the concept of residual networks and demonstrates that deeper residual networks have lower complexity and higher accuracy compared to VGG networks. Additionally, residual networks achieve a more straightforward training process.

3、模型架构

Plain Network
受VGG网络的影响，plain网络（如下图中间）的卷积层主要是3*3的滤波器，加权层的层数为34，在网络的最后是全局的平均pooling层和一个1000种类的包含softmax函数的全连接层。plain网络比VGG网络有更少的滤波器（卷积核后面的64，128，256等代表个数）和更低的计算复杂度，VGG-19模型有196亿个FLOPS，plain网络含有36亿个FLOPS。
Residual Network
在plain网络的基础上，加入shortcut连接，就变成了相应的残差网络，上图中所加实线表明可以直接使用恒等shortcuts，虚线表示维度不匹配时的情况，需要先调整维度再相加，调整维度的方法有两种：（A)仍然使用恒等映射，只是在增加的维度上使用0来填充，这种方法不会引入额外的参数；(B)使用1x1的卷积映射shortcut来调整维度保持一致。这两种方法都使用stride为2的卷积。

4、文献解读

一、Introduction

神经网络模型的深度对训练任务起着至关重要的作用，但是当模型深度太大时，会存在梯度消失/梯度爆炸的问题，尽管normalized initial-ization和intermediate normalization可以在一定程度上解决这个问题，但是准确率依然会在达到饱和后迅速退化，因此错误率甚至会更高，如下图所示，越深的网络有越高的训练错误率和测试错误率。

文章提出了深度残差学习（deep residual learning）框架来解决上图中的问题，如下图所示，通过前馈神经网络的shortcut connections来跨过一个层或者多个层，将前层的输出直接与卷积层的输出叠加，相当于做了个恒等映射。在极端情况下，如果恒等映射最优，可以将残差设置为0就简单地实现了恒等映射。简单来说，残差学习就是将一层的输入与另一层的输出结果一起作为一整个块的输出。

ResNet 之所以叫残差网络（Residual Network），是因为 ResNet 是由很多残差块（Residual Block）组成的。而残差块的使用，可以解决前面说到的退化问题。残差块如下图所示。

残差（residual）在数理统计中是指实际观察值（观测值）与估计值（拟合值）之间的差。
假设上图中的 weight layer 是 3×3 的卷积层；F(x) 表示经过两个卷积层计算后得到的结果；identity x 表示恒等映射（identity mapping），也称为shortcut connections。其实就是把 x 的值是不做任何处理直接传过去。最后计算 F(x)+x，这里的 F(x) 跟 x 是种类相同的信号，所以将其对应位置进行相加。我们让 H(x) = F(x)+x ，所以 H(x) 就是观测值，x 就是估计值。
我们如果使用plain networks（一般的卷积神经网络）那么 H(x) = F(x) ，这样某一层达到最优之后在加深就会出现退化问题。残差就体现在：F(x) = H(x)-x ，我们假设优化残差映射比优化原始的、未引用残差的映射更容易。在极端情况下，如果一个恒等映射 x 是最优的，那么将残差 F(x) 推到 0 比通过一堆非线性层来拟合一个恒等映射要容易得多。

二、实验

1、数据集

数据集：ImageNet 2012 classifi-cation dataset（1000类）
数据量：128 万张训练图像，5万张测试图像
标准：评估 top-1 和 top-5 错误率

2、参数设置

从一张图像或者它的水平翻转图像中随机采样一个224*224的crop，每个像素都减去均值。图像使用标准的颜色增强。我们在每一个卷积层之后，激活层之前均使用batch normalization（BN）。我们根据He2014spatial来初始化权值然后从零开始训练所有plain/残差网络。
我们使用的mini-batch的尺寸为256。学习率从0.1开始，每当错误率平稳时将学习率除以10，整个模型进行次迭代训练。我们将权值衰减设置为0.0001，a 动量为0.9。

3、实验结果

普通网络，结论：
（1）较深的 34 层普通网络比较浅的 18 层普通网络具有更高的验证误差。34 层普通网络在整个训练过程中具有较高的训练误差，尽管 18 层普通网络的解空间是 34 层网络的子空间。
（2）论文认为这种优化困难不是由梯度消失引起的。这些普通网络使用 BN 进行训练，确保前向传播的信号具有非零方差。我们还验证了反向传播的梯度在 BN 中表现出健康的范数。所以前向和后向信号都不会消失。事实上，34 层的普通网络仍然能够达到有竞争力的精度（表 3），这表明求解器在一定程度上起作用。我们推测深的普通网络的收敛速度可能呈指数级低，这会影响训练误差的减少。

ResNet，结论：
（1）34 层 ResNet 优于 18 层 ResNet（提高 2.8%）。更重要的是，34 层的 ResNet 表现出相当低的训练误差，并且可以推广到验证数据。这表明退化问题在此设置中得到了很好的解决，可以通过增加深度来获得准确度。
（2）相比普通网络ResNet 将 top-1 误差降低了 3.5%（表 2），这是由于成功降低了训练误差。这种比较验证了残差学习在极深系统上的有效性。
（3）我们还注意到 18 层的普通/残差网络相当准确，但 18 层的 ResNet 收敛速度更快。当网络“不太深”（此处为 18 层）时，当前的 SGD 求解器仍然能够为普通网络找到好的解决方案。在这种情况下，ResNet 通过在早期提供更快的收敛来简化优化。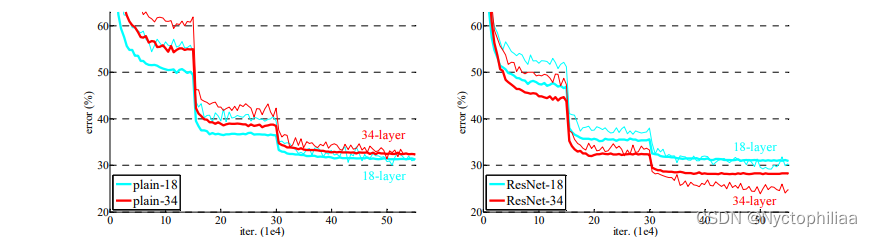

三、结论

残差结构的主要作用是传递信号，把深度学习浅层的网络信号直接传给深层的网络。深度学习中不同的层所包含的信息是不同的，一般我们认为深层的网络所包含的特征可能对最后模型的预测更有帮助，但是并不是说浅层的网络所包含的信息就没用，深层网络的特征就是从浅层网络中不断提取而得到的。现在我们给网络提供一个捷径，也就是Shortcut Connections，它可以直接将浅层信号传递给深层网络，跟深层网络的信号结合，从而帮助网络得到更好的效果。

二、PINN

一、PINN比传统数值方法有哪些优势

PINN是一种（深度）网络，在定义时空区域中给定一个输入点，在训练后在微分方程的该点中产生估计的解。结合对控制方程的嵌入得到残差，利用残差构造损失项。本质原理就是将方程（物理知识）集成到网络中，并使用来自控制方程的残差项来构造损失函数，由该项作为惩罚项来限制可行解的空间。用PINN来求解方程并不需要有标签的数据，比如先前模拟或实验的结果。PINN算法本质上是一种无网格技术，通过将直接求解控制方程的问题转换为损失函数的优化问题来找到偏微分方程解。

1、传统数值方法主要针对复杂问题的正计算，比如说已知边界条件、已知控制方程的正计算，在正计算上，深度学习的方法逊色一些，但是针对一些反问题，比如说一些测量数据和部分物理(方程中某些参数未知、边界条件未知)，深度学习方法可以形成数据和物理双驱动的模型，比传统数值方法的效率更高。

2、当面对一些数值问题时，PINN可以不需要用数值格式去推导求解，可以直接利用加物理损失的方法得到一个参考解，当问题边界需要不停地换时，或者很多资源不停的变化的情况下，如果利用大量时间去训练一个网络，在推断阶段可以实现快速预测。

二、PINN方法

先构建一个输出结果为 $eq?%5Cwidehat%7Bu%7D$ 的神经网络，将其作为PDE解的代理模型，将PDE信息作为约束，编码到神经网络损失函数中进行训练。损失函数主要包括4部分：偏微分结构损失(PDE loss)，边值条件损失(BC loss)、初值条件损失(IC loss)以及真实数据条件损失(Data loss)。

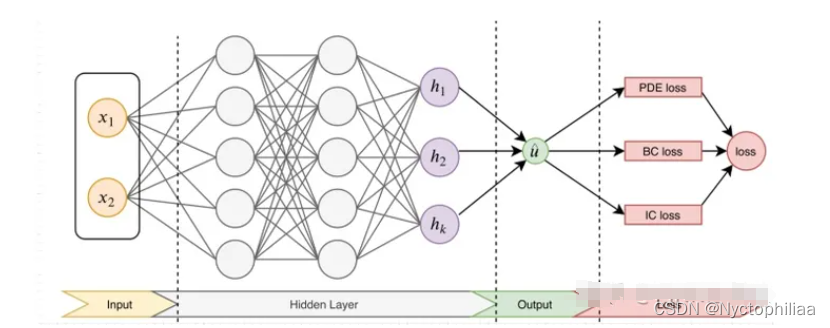
后，利用梯度优化算法最小化损失函数，直到找到满足预测精度的网络参数 $eq?%5Ctheta%20%5E%7B*%7D$ 。

对于逆问题(即方程中的某些参数未知)，若只知道PDE方程及边界条件，PDE参数未知，该问题为非定问题，所以必须要知道其他信息，如部分观测点u的值。此时，PINN做法可将方程中的参数作为未知变量，加到训练器中进行优化，损失函数包括Data loss。

三、正问题与反问题

正问题和反问题的正经定义可以解释为：正问题，已知原因，根据已有的模型和规律，得到结果状态或者观测，而反问题则是已知结果状态或者观测，来反推原因。正问题例子包括设计飞机的方案参数，然后通过模拟，可以知道飞机的性能，反问题则是根据飞机的设计需求，反推应该给什么设计方案。因此，工程界通常称正问题为模拟问题，反问题为设计问题。对于一个PDE方程，我们这样来定义正问题，已知PDE方程，求解PDE方程在场域内的解为正问题；反问题我们定义为，已知一些场域内的观测情况，来反推最优的PDE方程的系数/参数的值。

对于PDE问题而言，PINN的正问题就是根据已有的PDE来求解场域内的解。建立一个神经网络 $eq?G$ ，来学习PDE的特性。具体来说，就是建立时间坐标 $eq?t$ 和空间坐标 $eq?x$ 与解 $eq?y$ 的映射，即： $eq?G%3At%2Cx%5Crightarrow%20y$ 。

神经网络的训练需要一个目标函数，PDE方程其实就是一个损失函数，如果不满足等式关系，就会产生损失，因此，把神经网络的 $eq?t%2Cx%2C%5Cwidehat%7By%7D%3DG%28t%2Cx%29$ 放进PDE里面获取损失。

从数学角度看，和传统的机器学习相比，它最大的不同就是在要求0阶常数项与系统一致的基础上，同时要求高阶梯度项与系统一致。从泰勒展开的角度来看，它显然具有更高的精度，因为它更满足系统的高维特征。从机器学习和问题的适配角度来看，采用神经网络而不是别的机器学习方法也是非常有见地的设计，因为神经网络的可微性带来了梯度求解的可行性。求解正问题时，PINN完全不需要数据，只需要随意在空间和时间步上采样，然后让PDE方程来评估神经网络的建模是否准确；或者说真实数据是基于PDE损失函数的中间量。

PINN 解反问题的任务是需要反推出PDE中的各项的超参数。这个问题的设定意味着我们没有真实可靠的PDE方程来做评判，因此，需要实际的观测（场域的值）来提供损失函数。简而言之，我们就是在一族的PDE中挑一个最合适的来拟合实际的系统。

三、PINN实验

一、数学方程

使用一个最简单的常微分方程：

$eq?%7Bf%7D%27%28x%29%3Df%28x%29$

$eq?f%280%29%3D1$

这个微分方程其实就是：

$eq?f%28x%29%3De%5E%7Bx%7D$

二、模型搭建

核心-使用最简单的全连接层：

class Net(nn.Module):
    def __init__(self, NL, NN): # NL n个l（线性，全连接）隐藏层， NN 输入数据的维数，
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(1, NN)
        self.hidden_layer = nn.linear(NN,int(NN/2)) ## 原文这里用NN，我这里用的下采样，经过实验验证，“等采样”更优。更多情况有待我实验验证。
        self.output_layer = nn.Linear(int(NN/2), 1)

    def forward(self, x):
        out = torch.tanh(self.input_layer(x))
        out = torch.tanh(self.hidden_layer(out))
        out_final = self.output_layer(out)
        return out_final

偏微分方程定义，也就是第一个公式：

def ode_01(x,net):
    y=net(x)
    y_x = autograd.grad(y, x,grad_outputs=torch.ones_like(net(x)),create_graph=True)[0]
    return y-y_x   # y-y' = 0

源码：

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from torch import autograd

"""
用神经网络模拟微分方程,f(x)'=f(x),初始条件f(0) = 1
"""

class Net(nn.Module):
    def __init__(self, NL, NN): # NL n个l（线性，全连接）隐藏层， NN 输入数据的维数，
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(1, NN)
        self.hidden_layer = nn.Linear(NN,int(NN/2)) ## 原文这里用NN，我这里用的下采样，经过实验验证，“等采样”更优。更多情况有待我实验验证。
        self.output_layer = nn.Linear(int(NN/2), 1)

    def forward(self, x):
        out = torch.tanh(self.input_layer(x))
        out = torch.tanh(self.hidden_layer(out))
        out_final = self.output_layer(out)
        return out_final


net=Net(4,20) # 4层 20个
mse_cost_function = torch.nn.MSELoss(reduction='mean') # Mean squared error 均方误差求
optimizer = torch.optim.Adam(net.parameters(),lr=1e-4)  # 优化器

def ode_01(x,net):
    y=net(x)
    y_x = autograd.grad(y, x,grad_outputs=torch.ones_like(net(x)),create_graph=True)[0]
    return y-y_x   # y-y' = 0

# requires_grad=True).unsqueeze(-1)

plt.ion()  # 动态图
iterations=200000
for epoch in range(iterations):

    optimizer.zero_grad()  # 梯度归0

    ## 求边界条件的损失函数
    x_0 = torch.zeros(2000, 1)
    y_0 = net(x_0)
    mse_i = mse_cost_function(y_0, torch.ones(2000, 1))  # f(0) - 1 = 0

    ## 方程的损失函数
    x_in = np.random.uniform(low=0.0, high=2.0, size=(2000, 1))
    pt_x_in = autograd.Variable(torch.from_numpy(x_in).float(), requires_grad=True)  # x 随机数
    pt_y_colection=ode_01(pt_x_in,net)
    pt_all_zeros= autograd.Variable(torch.from_numpy(np.zeros((2000,1))).float(), requires_grad=False)
    mse_f=mse_cost_function(pt_y_colection, pt_all_zeros)  # y-y' = 0

    loss = mse_i + mse_f
    loss.backward()  # 反向传播
    optimizer.step()  # 优化下一步。This is equivalent to : theta_new = theta_old - alpha * derivative of J w.r.t theta

    if epoch%1000==0:
            y = torch.exp(pt_x_in)  # y 真实值
            y_train0 = net(pt_x_in) # y 预测值
            print(epoch, "Traning Loss:", loss.data)
            print(f'times {epoch}  -  loss: {loss.item()} - y_0: {y_0}')
            plt.cla()
            plt.scatter(pt_x_in.detach().numpy(), y.detach().numpy())
            plt.scatter(pt_x_in.detach().numpy(), y_train0.detach().numpy(),c='red')
            plt.pause(0.1)

结果展示：

训练0次时的结果也就是没训练，蓝色是真实值、红色是预测值：

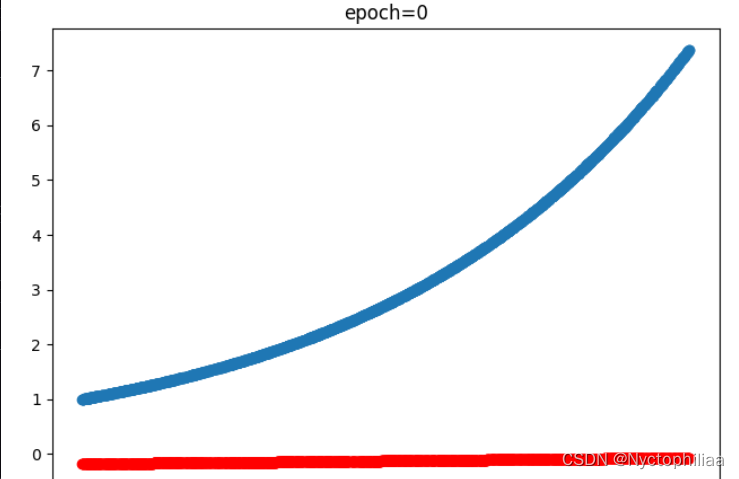
训练2000次时的结果，蓝色是真实值、红色是预测值：

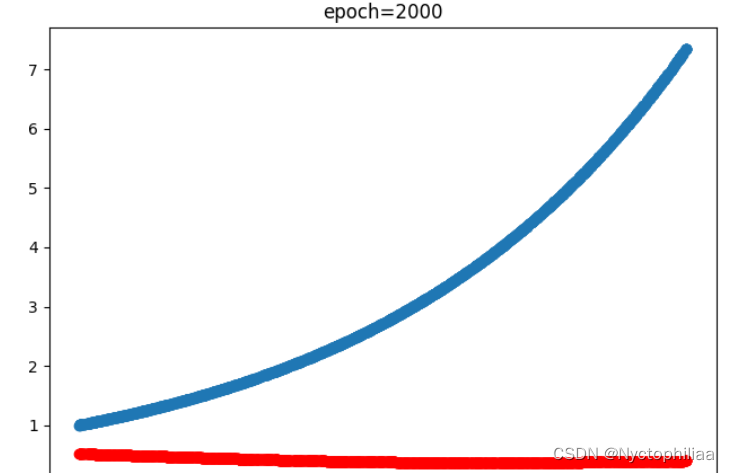
训练20000时的结果，蓝色是真实值、红色是预测值，不过红色已经完全把蓝色覆盖了，也就是完全拟合了：

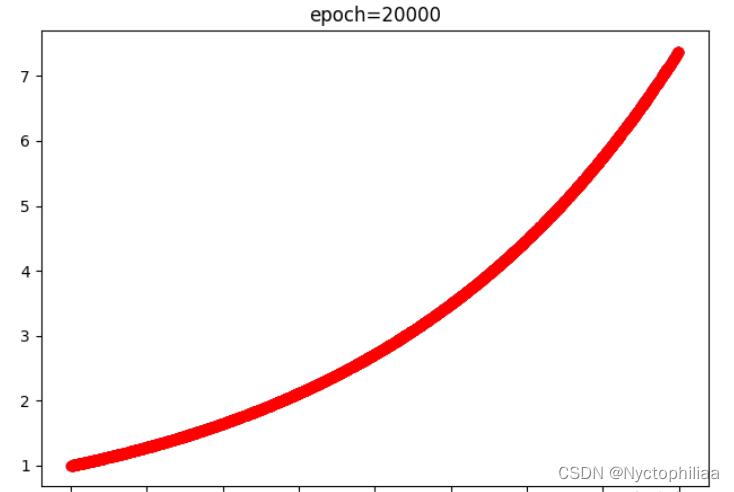
总结

ResNet网络的最初原始论文说明：一味地加深网络深度会使得网络达到了一种饱和状态（论文中强调不是过拟合现象，而是一种网络深度到一定程度之后的退化问题），而导致精度的下降。PINN的原理就是通过训练神经网络来最小化损失函数来近似PDE的求解，所谓的损失函数项包括初始和边界条件的残差项，以及区域中选定点（按传统应该称为"配点"）处的偏微分方程残差。