目录
题目:
我们直接看题解吧:
快速理解解题思路小建议:
审题目+事例+提示:
解题方法:
解题分析:
解题思路:
代码实现(DFS):
代码1:
补充说明:
代码2:
代码实现(BFS):
题目地址:
199. 二叉树的右视图 - 力扣(LeetCode)
难度:中等
今天刷二叉树的右视图,大家有兴趣可以点上面链接,看看题目要求,试着做一下。
题目:
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
我们直接看题解吧:
快速理解解题思路小建议:
可以先简单看一下解题思路,然后照着代码看思路,会更容易理解一些。
审题目+事例+提示:
根据题意可知,我们右视图看到的节点都是每一层的最右边的节点,而这个节点可能在右子树,也可能子左子树
解题方法:
方法1:深度优先(DFS)
方法2:广度优先(BFS)
解题分析:
我们利用深度优先算法递归遍历二叉树,按照【根节点->右子树->左子树】的顺序访问。
解题思路:
创建一个list集合res用于存储右视图看到的节点(即每层最右边的节点)
创建一个临时遍历depth,用于记录遍历树的深度
递归函数:
首先判断如果根节点为Null,则直接返回
接着判断depth与res.size是否相等,相等则将当前节点加入res
然后depth++,遍历右子树、左子树
代码实现(DFS):
代码1:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
//DFS深度优先算法
class Solution {
//先创建一个list集合存储数据作为返回
List<Integer> res = new ArrayList<Integer>();
public List<Integer> rightSideView(TreeNode root) {
//传入根节点root,以及0(即depth初始为0)
dfs(root,0);
return res;
}
public void dfs(TreeNode root,int depth){
//先判断,1、根节点是否为null,如果根节点为null则返回,
// 2、同时也是递归的终止条件,即访问到叶子结点的下一个的时候为null,则返回
if(root == null){
return;
}
//首先先访问当前结点,再递归地访问右子树 和 左子树
if(depth == res.size()){//判断二者是否相等,相等则将当前节点加入集合res
res.add(root.val);
}
//每递归一次就说明走到下一层,即深度+1
depth++;
//先递归右子树,再递归左子树,这样每一层都能访问到最右边的结点
dfs(root.right,depth);
dfs(root.left,depth);
}
}补充说明:
1、递归函数第一部分的判空操作的作用
a.根节点判空条件,即如果根节点为null则返回,
b.作为递归的终止条件,即访问到叶子结点的下一个的时候为null,则返回2、实际上遍历完右子树,回过头遍历左子树的时候,depth实际上是从头计算的,因为一开始遍历右子树时,每一次递归depth+1,那么最后回溯时depth相当于depth+1直到根节点
2、为什么depth==res.size时,就将当前节点添加到集合res(还是无法理解可以看看下面代码2)
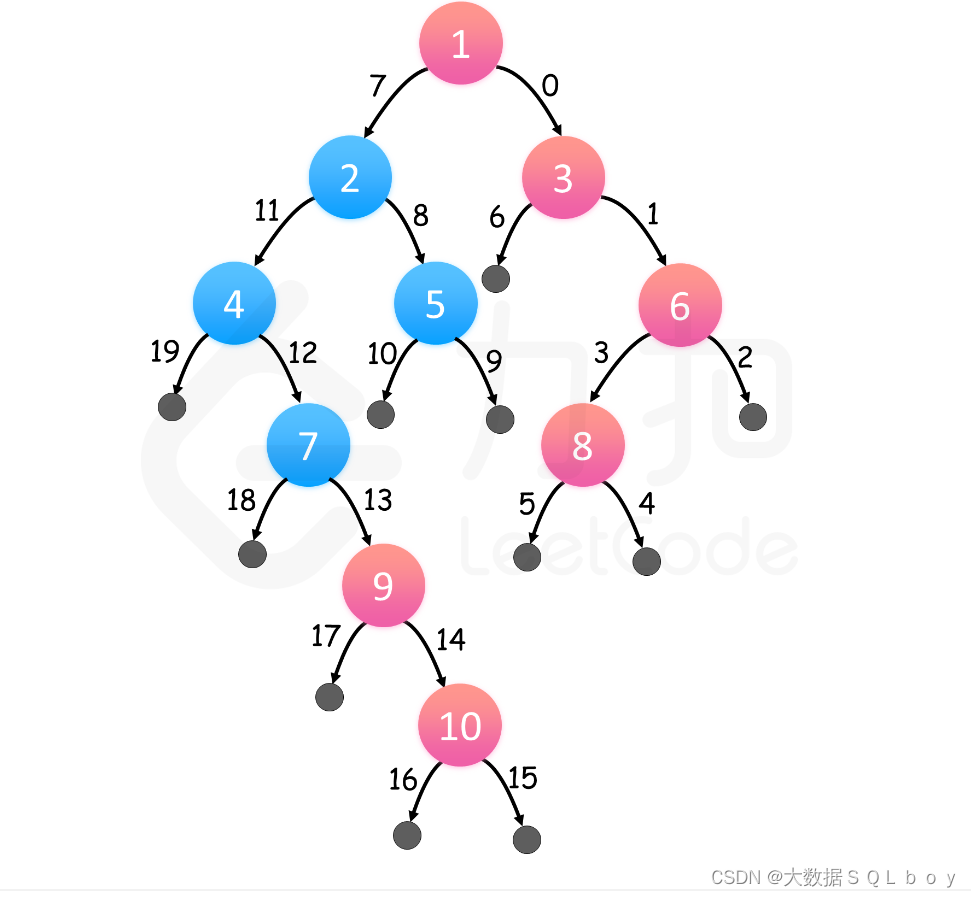
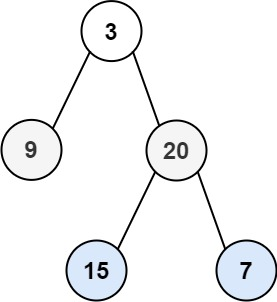
以此图为例
首先遍历右子树,depth和res.size初始值均为0,根据代码自上而下的执行顺序,res.size首先+1即添加根节点,接着时depth+1,进入下一层,此时res.size==depth==1,因此添加当前节点,接着depth+1...
遍历完右子树后,遍历左子树,由于depth从0开始,在同一层时,depth与res.size差1,这样就可以更新新的节点(即depth!=res.size时说明这一层已经有值在res了),同时又能保证每一层只会取到一个节点,(此外由于遍历顺序为根右左,因此保证了每层最先遍历的时最右边的节点)
代码2:
这个的跟上面区别在于用了两个变量,一个变量maxDepth记录已探索到的最大深度,和当前的深度depth,只有depth>maxDepth才往list里面add即可。这种可能更好理解一点
class Solution {//0ms 100% On O1
int maxHigh = 0;
List<Integer> res = new ArrayList<Integer>();
public List<Integer> rightSideView(TreeNode root) {
dfs(root,1);
return res;
}
public void dfs(TreeNode root,int high){
if(root == null) return;
if(maxHigh < high){
res.add(root.val);
maxHigh = high;
}
dfs(root.right,high+1);
dfs(root.left,high+1);
}
}代码实现(BFS):
这里BFS实际上是层次遍历,然后将每层的最后一个节点加入集合
还有就是创建了一个队列queue用于存储每层遍历的节点
层次遍历-->二叉树的层序遍历,力扣-CSDN博客
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (i == size - 1) { //将当前层的最后一个节点放入结果列表
res.add(node.val);
}
}
}
return res;
}
}