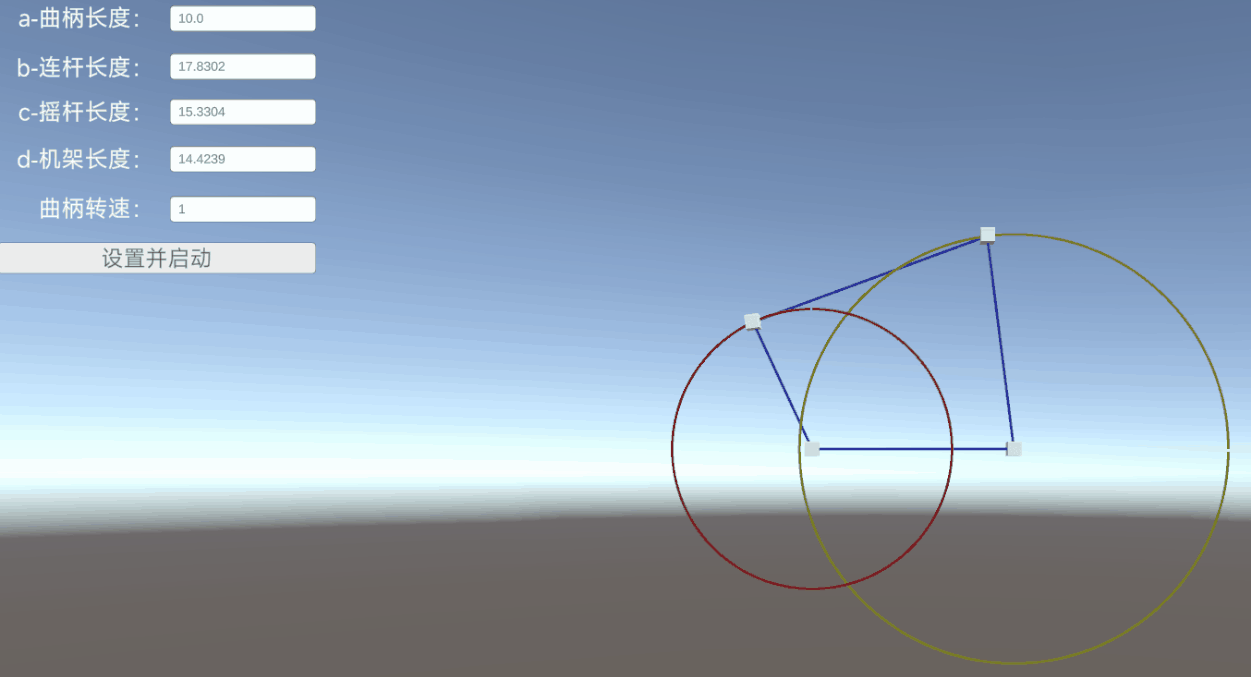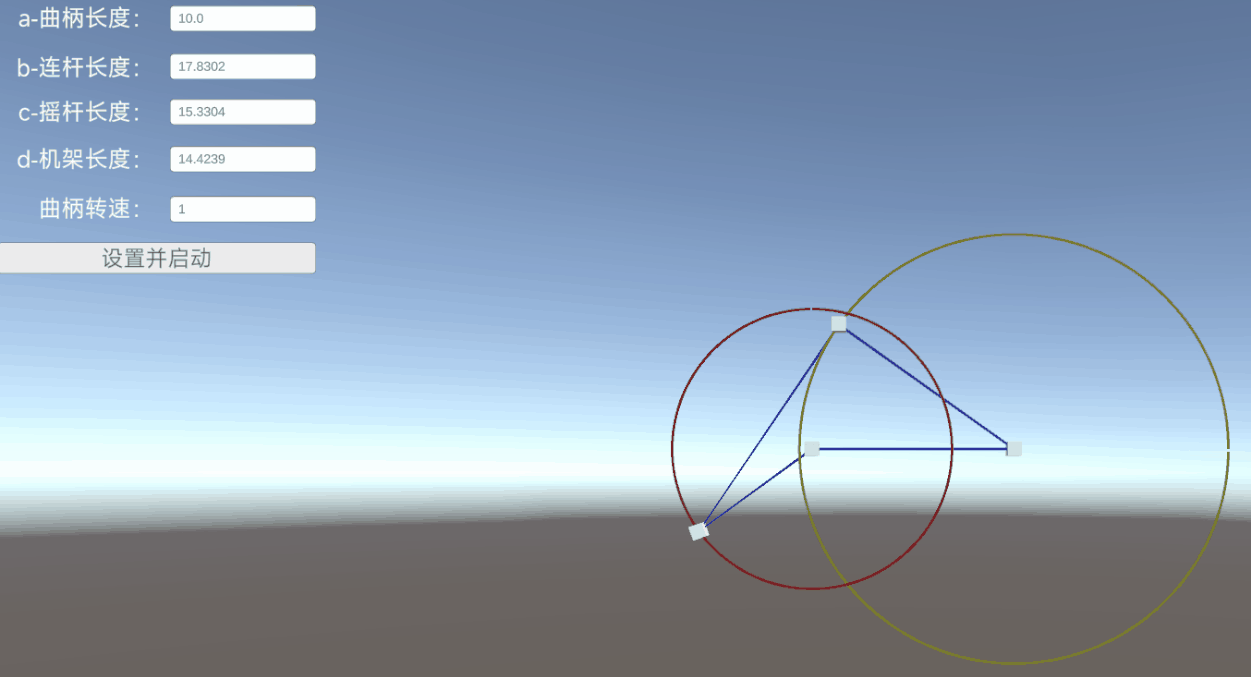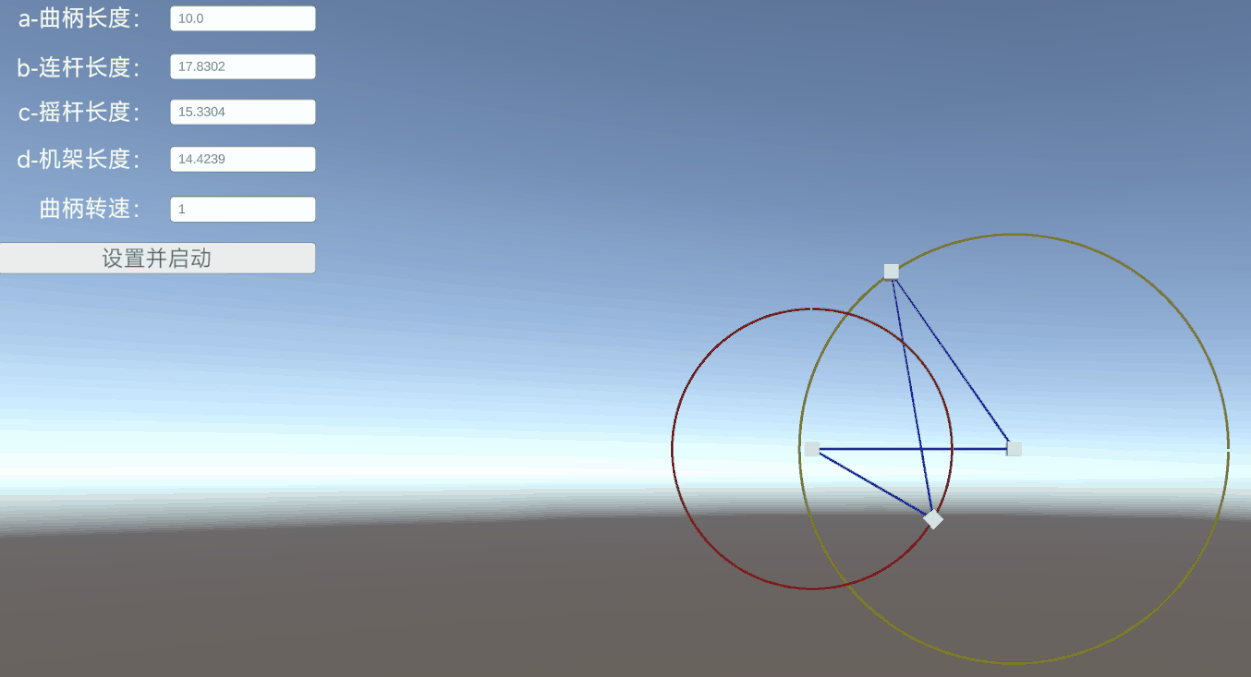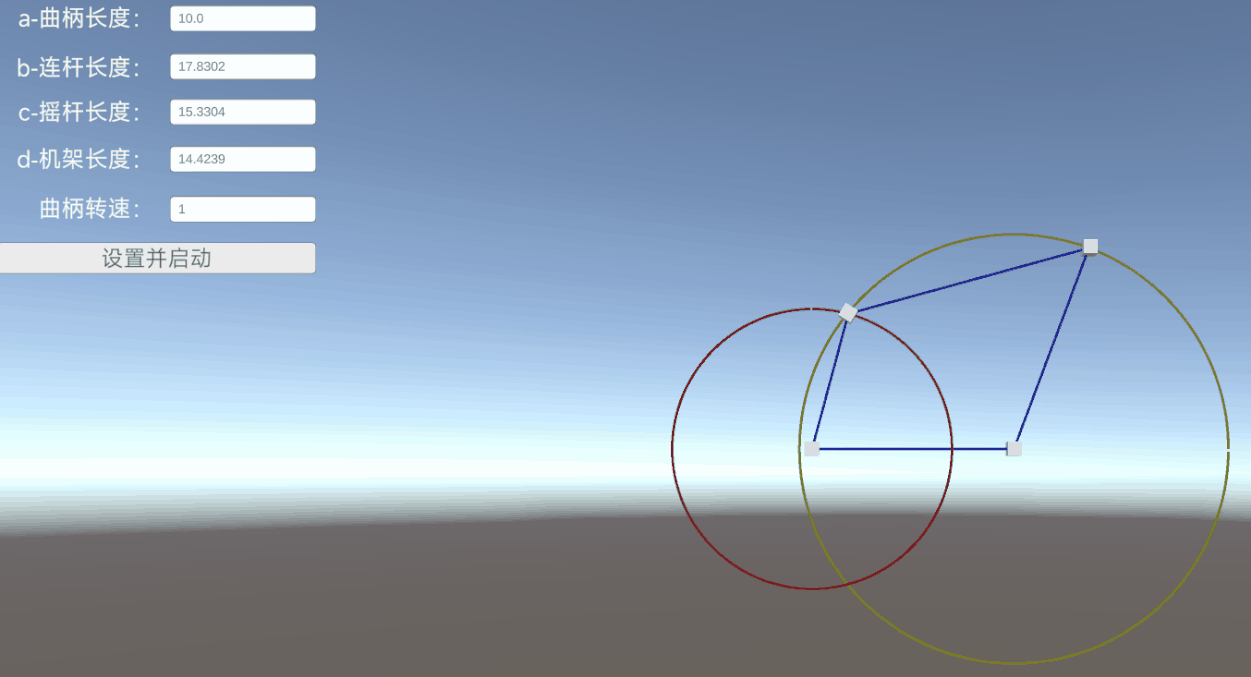
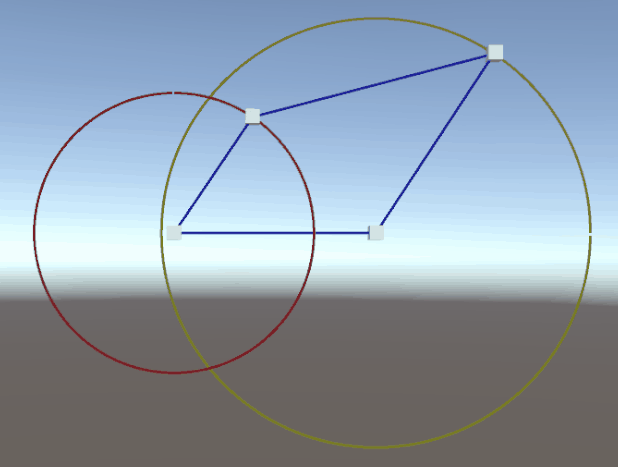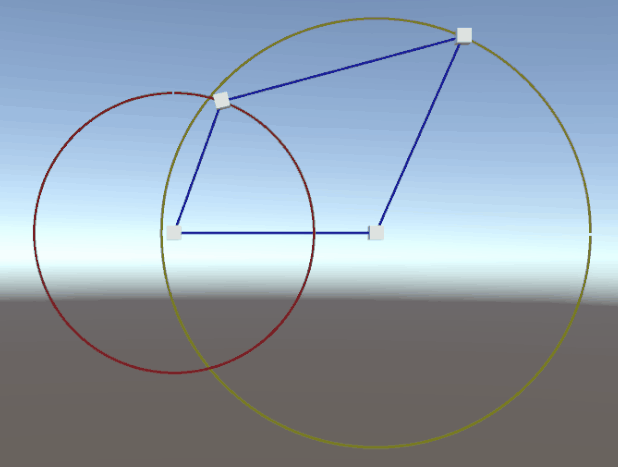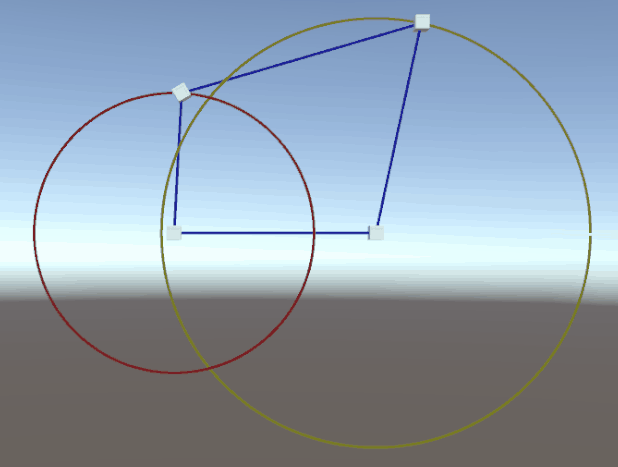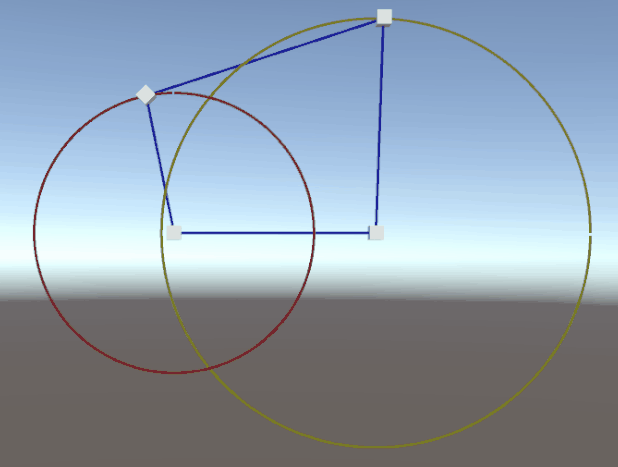
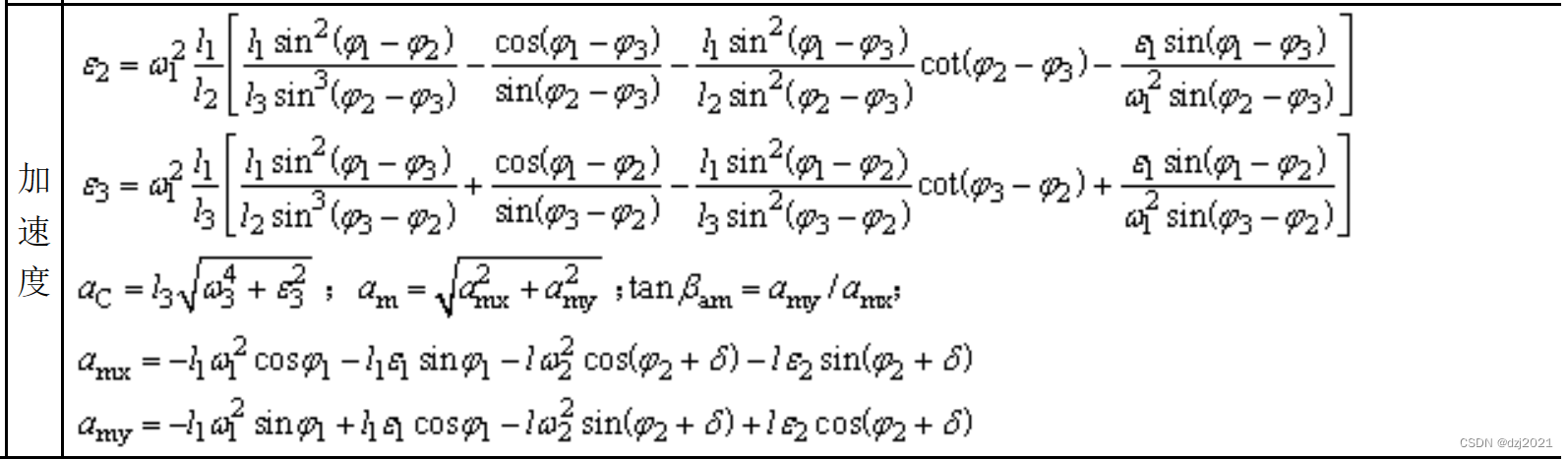一、效果图
设定好各边长度和转速后,点击【设置并启动】,自动生成一个机构模型,并按照原理进行运转
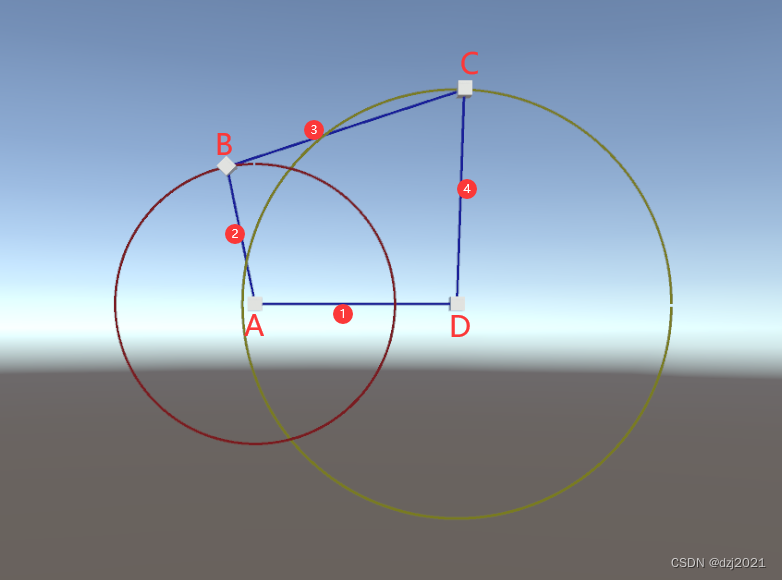
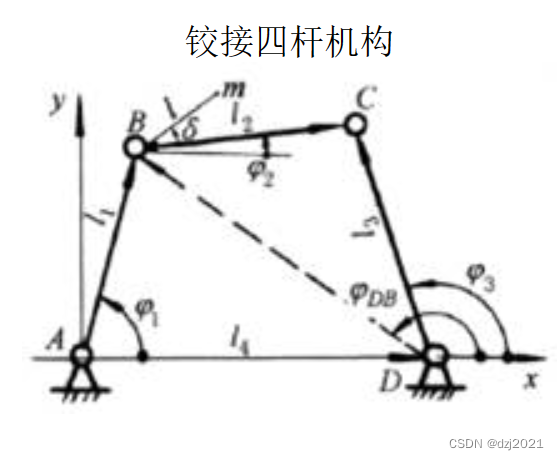
二、铰链四杆机构介绍
机架:A和D是固定位置,叫做机架。
曲柄:B点绕A点旋转,构成曲柄。
连杆:C点和B点相连,构成连杆。
摇杆:C点绕着D点转动,构成摇杆。
三、运动原理
1、机构示意图
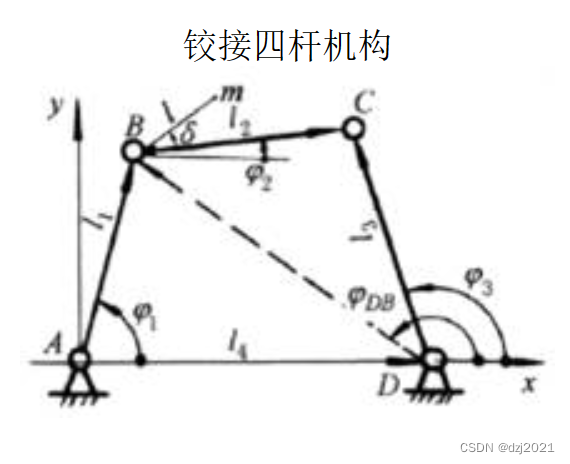
第一步:计算Φ1(∠BAD)
曲柄转动了多少度
第二步:计算BD的长度
已知B点和D点位置,计算BD的长度,可用机械公式计算,或者直接使用Vector3.Distance计算。
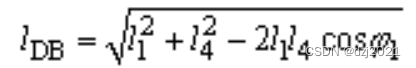
第三步:计算∠ΦDB(∠BDA’)
-
(1)用机械原理公式计算的依据:
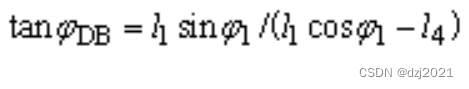
-
(2)直接用Unity向量距离api计算:
Vector3.Distance(A, D);//示例代码
第四步:计算计算∠Φ3的值
只能用机械原理的公式计算:
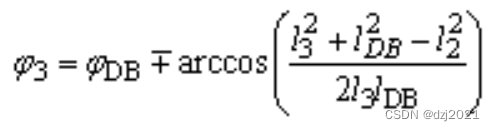
第五步:根据∠Φ3计算C点位置
∠Φ3已知的时候,在射线DC上取C点
四、关键代码实现
代码为计算部分的代码,仅供交流学习之用。
/// <summary>
/// 计算曲柄和摇杆位置
/// </summary>
/// <returns></returns>
bool JiSuanWeiZhi()
{
//设定B的位置 AB = a
var posB = A.transform.position + (B.transform.position - A.transform.position).normalized * (float)a_AB;
B.transform.position = posB;
//计算Φ1(∠BAD)
double phi1 = Vector3.Angle(B.transform.position - A.transform.position, D.transform.position - A.transform.position);
//象限判断
if (B.transform.position.y < A.transform.position.y)
{
phi1 = 360 - phi1;
}
//公式计算lenDB的值
var lDB2 = math.sqrt(a_AB * a_AB + d_DA * d_DA - 2 * a_AB * d_DA * Cos(phi1.ToRadians()));
//计算ΦDB(∠BDA')
double phiDB = Vector3.Angle(B.transform.position - D.transform.position, D.transform.position - A.transform.position);
//象限处理
if (B.transform.position.y < A.transform.position.y)
{
phiDB = 360 - phiDB;
}
//计算Φ3的值
var phi3 = phiDB - Acos((c_CD*c_CD + lDB2 * lDB2 - b_BC * b_BC)/(2 * c_CD * lDB2)).ToDegrees();
//摆放C点
if (double.IsNaN(phi3))
{
Debug.Log($"无法计算Φ3的值 {(c_CD*c_CD + lDB2 * lDB2 - b_BC * b_BC)/(2 * c_CD * lDB2)}");
return false;
}
else
{
Quaternion q = Quaternion.AngleAxis((float)phi3, new Vector3(0,0,1));
var dir = q * (D.transform.position - A.transform.position);
C.transform.position = D.transform.position + dir.normalized * (float)c_CD;
}
return (true);
}
五、机械原理附录:
1、平面示意图
2、运动分析公式——位置计算
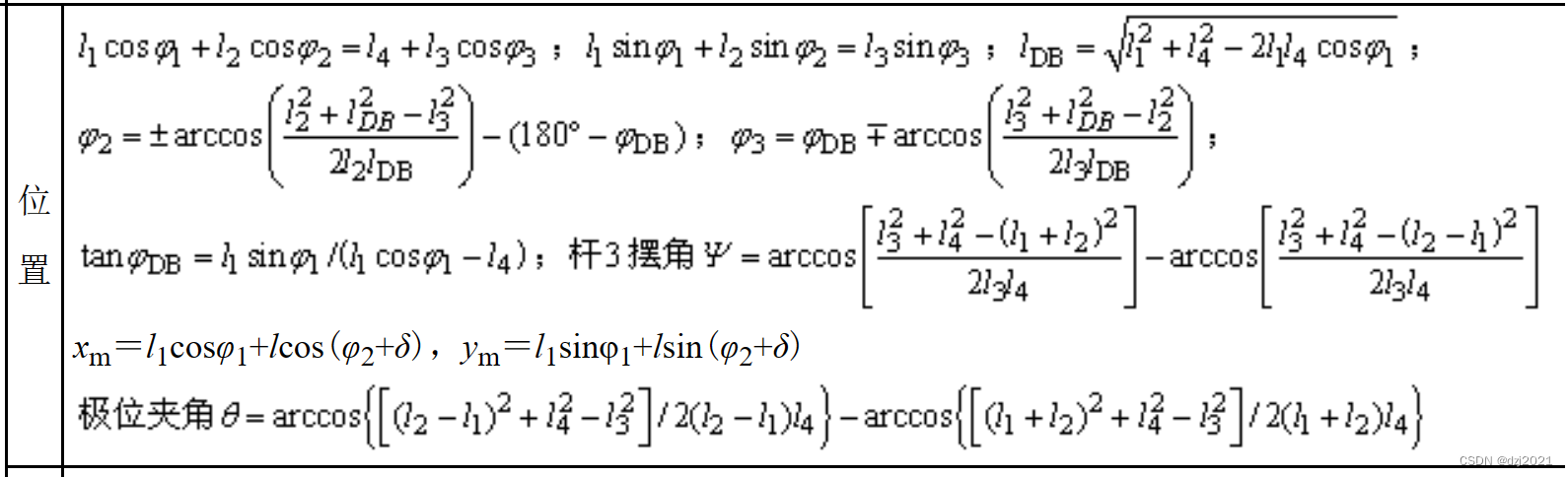
3、运动分析公式——速度计算
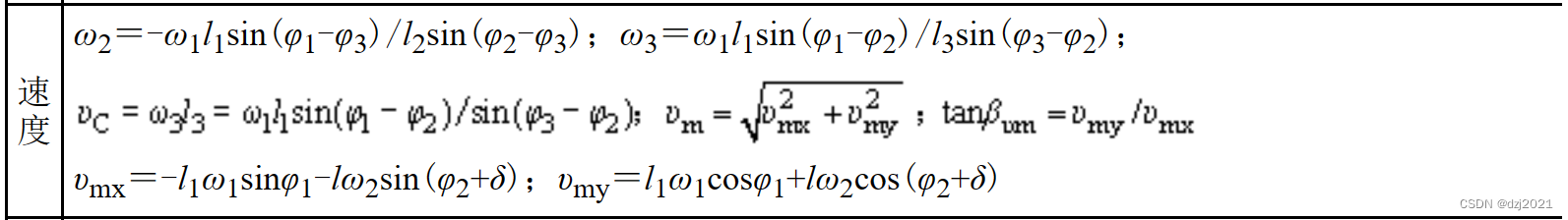
4、运动分析公式——加速度计算