scikit-learn 普通最小二乘法
- 什么是普通最小二乘法?
- 参考文献
什么是普通最小二乘法?
线性回归模型的数学表达式如下:
y ^ ( w , x ) = w 0 + w 1 x 1 + … + w p x 1 \hat{y}(w, x)=w_{0}+w_{1} x_{1}+\ldots+w_{p} x_{1} y^(w,x)=w0+w1x1+…+wpx1
其中 w 0 , w 1 , . . . , w p w_0,w_1,...,w_p w0,w1,...,wp 为模型参数, x 1 , x 2 , . . . , x p x_1,x_2,...,x_p x1,x2,...,xp 为特征(feature)也称自变量。
最小二乘法就是找到一组最佳参数 w ^ 0 , w ^ 1 . . . , w ^ p \hat w_0, \hat w_1...,\hat w_p w^0,w^1...,w^p 使得真实的 y \boldsymbol y y 和我们通过参数 w \textbf w w 及特征 x \textbf x x 计算的 y ^ \boldsymbol{\hat y} y^ 的欧式距离最小。
其实也就是求解下面的优化问题:
min w ∥ X w − y ∥ 2 2 \min _{w}\|X w-y\|_{2}^{2} wmin∥Xw−y∥22
至于优化问题的求解方式,有很多种,我们先用 sklearn 帮我们解决。
以下为 scikit-learn 官方文档示例:
# 从 sklearn 中引入线性模型模块
from sklearn import linear_model
# 建立线性回归对象 reg
reg = linear_model.LinearRegression()
# 通过建立的对象拟合数据 x 为 [[0, 0], [1, 1], [2, 2]], y 为 [0, 1, 2]
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
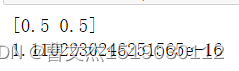
# 拟合的参数系数如下 y = 1.1102230246251565e-16 + 0.5x1 + 0.5x2
print(reg.coef_)
print(reg.intercept_)
参考文献
https://scikit-learn.org/stable/modules/linear_model.html