参考labuladong的算法小抄整理 link
子序列问题,用一维dp数组或二维dp数组来解决。
- 一维数组:最大子数组和,最长递增子序列。dp[i]的定义:在子数组 arr[0…i] 中,以 arr[i] 结尾的子序列的长度是 dp[i]。
- 二维数组:主要用于两个数组的情况,如编辑距离,最大公共子序列;也有用在一个数组的情况,比如最长回文子序列
for i in range(n):
for j in range(n):
if arr[i] == arr[j]:
dp[i][j] = dp[i][j] + ... #累计相同元素的贡献
else:
dp[i][j] = min(...) #替换为适当的函数或计算方法,更新dp[i][j]的值为选取最大的贡献
二维dp 数组的定义
涉及两个字符串/数组的场景:
在子数组 arr1[0…i] 和子数组 arr2[0…j] 中,我们要求的子序列长度为 dp[i][j]。
只涉及一个字符串/数组的场景:
在子数组 array[i…j] 中,我们要求的子序列的长度为 dp[i][j]
1. 最长递增子序列
力扣300题:https://leetcode.cn/problems/longest-increasing-subsequence/description/
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
注意:子序列不一定是连续的。
方法1:动态规划
class Solution(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
# dp[i]的含义为以nums[i]结尾的最长递增子序列长度。初始化为1,因为LIS必须包括自身。
dp = [1] * n
for i in range(n):
for j in range(0, i):
if nums[j] < nums[i]:
dp[i] = max(dp[i], dp[j]+1)
res = 0
for i in range(n):
res = max(res, dp[i])
return res
时间复杂度:O(n^2)
方法2:二分查找
时间复杂度O(nlogn)
核心思路:贪心,LIS需要让序列上升地尽量慢
数组d[i]的定义:长度为i的最长上升子序列中,末尾元素最小的值。可以证明d是单调递增的。
需要一个lowerBound函数,寻找在d中第一个比nums[i]小的值。更多二分查找参考:
class Solution(object):
def lowerBound(self, d, left, right, target):
while left <= right:
mid = left + (right-left)//2
if d[mid] == target:
right = mid - 1
elif d[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# 贪心思想:LIS需要让序列上升地尽量慢
n = len(nums)
if n <= 0:
return 0
d = [0 for _ in range(n+1)] # d[i]表示长度为i的最长上升子序列中,末尾元素最小的值。
# 可以证明d[]是单调递增的。
length = 1
d[length] = nums[0]
for i in range(1, n):
if nums[i] > d[length]:
d[length+1] = nums[i]
length += 1
else:
# 在数组d[1,...,length]中二分查找,找到nums[i]的lowerBound
#(如果nums[i]在d中不存在,则返回第一个比nums[i]小的数字的index),
# 并更新d[length] = nums[i]
idx = self.lowerBound(d, 1, length, nums[i])
d[idx] = nums[i]
return length
2. 最大子数组
leetcode 53题 最大子数组和
https://leetcode.cn/problems/maximum-subarray/
滑动窗口思路
双指针从0,0开始。当窗口内的子数组和>=0时,往右扩大窗口;<0时从左边缩小窗口。
为什么:因为有正有负的情况下,最大子数组一定是以正数开头的。所有以上的方式就是穷举所有以正数开头的子数组。
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
if n == 0:
return 0
left, right = 0, 0
windowSum, res = 0, float('-inf')
while right < n:
windowSum += nums[right]
res = max(res, windowSum)
right += 1
while windowSum < 0:
windowSum -= nums[left]
left += 1
return res
动态规划思路
dp[i]: 以nums[i]结尾的最大子数组的和
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
dp = [nums[i] for i in range(n)]
for i in range(1, n):
if(dp[i-1] > 0):
dp[i] = dp[i-1]+nums[i]
res = float('-inf')
for item in dp:
res = max(res, item)
return res
3. 最长公共子序列
leetcode 1143
https://leetcode.cn/problems/longest-common-subsequence/
dp[i][j]: s1[0:i]和s2[0:j]的lcs长度.(这里0:i是左闭右开)
- 当s1[i-1] == s2[j-1]时,直接对dp[i-1][j-1] +1即可
- 当s1[i-1] == s2[j-1]时,直接却dp[i-1][j]和dp[i][j-1]的最大值
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
"""
:type text1: str
:type text2: str
:rtype: int
"""
m = len(text1)
n = len(text2)
dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if(text1[i-1] == text2[j-1]):
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n]
复杂度:O(mn), O(mn)
优化空间复杂度到O(n):
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
"""
:type text1: str
:type text2: str
:rtype: int
"""
m = len(text1)
n = len(text2)
dp = [0 for _ in range(n+1)]
tmp1, tmp2 = 0, 0 //
for i in range(1, m+1):
tmp2 = 0
for j in range(1, n+1):
tmp1 = dp[j]
if(text1[i-1] == text2[j-1]):
dp[j] = tmp2+1
else:
dp[j] = max(dp[j], dp[j-1])
tmp2 = tmp1 # tmp2记录上一次dp的数值
return dp[n]
4. 最长回文子序列
leetcode 516
https://leetcode.cn/problems/longest-palindromic-subsequence/
兄弟题目:最长回文子串https://leetcode.cn/problems/longest-palindromic-substring/
-
dp[i][j]的定义:s[i:j]的最长回文子序列长度
-
dp初始化:对角线上是1,i > j的时候是0
-
遍历方向:dp[i][j]只跟左、下、左下3个元素有关,所以是从下往上,从左往右遍历。
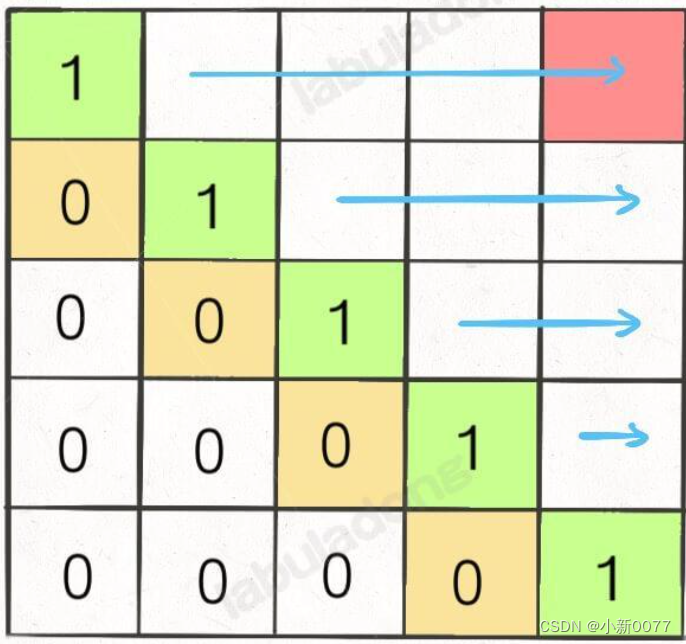
-
复杂度: O(n^2), O(n^2)
class Solution(object):
def longestPalindromeSubseq(self, s):
"""
:type s: str
:rtype: int
"""
n = len(s)
dp = [[0 for _ in range(n)] for _ in range(n)]
for i in range(n):
dp[i][i] = 1
for i in range(n-2, -1, -1):
for j in range(i+1, n):
if (s[i] == s[j]):
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
return dp[0][n-1]
5. 编辑距离
https://leetcode.cn/problems/edit-distance/
二维dp, size为m+1, n+1,第一个位置是空字符

- dp数组的含义:dp[i][j]指s1[0…i)(左闭右开)和s2[0…j)两个字符串之间的编辑距离。 dp[0][0] = 0 指s1和s2都为空字符串,
- base case:dp[0][i] = i, dp[j][0] = j. 当其中一个字符串为空时,编辑距离只用增加字符即可
- 状态转移:dp[i][j]只和dp[i][j-1],dp[i-1][j], dp[i-1][j-1]有关,分两种情况讨论
- s[i-1] == s[j-1], 此时不用做任何操作,所以dp[i][j] = dp[i-1][j-1]
- s[i-1] != s[j-1], 有三种操作方式:增、删、替换,对应dp[i][j-1]+1,dp[i-1][j]+1, dp[i-1][j-1]+1,取三者中的最小值即为dp[i][j]的值
class Solution(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
m, n = len(word1), len(word2)
dp = [[0] * (n+1) for _ in range(m+1)]
# print(dp)
for i in range(1, m+1):
dp[i][0] = i
for i in range(1, n+1):
dp[0][i] = i
for i in range(1, m+1):
for j in range(1, n+1):
if (word1[i-1] == word2[j-1]):
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+1)
# for x in dp:
# print(x)
return dp[m][n]
时间复杂度:O(mn), 空间复杂度:O(mn)
降低空间复杂度
dp[i][j]只和3个相邻的元素有关,所以可以优化为O(min(m, n))的空间复杂度