现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

示例 1：

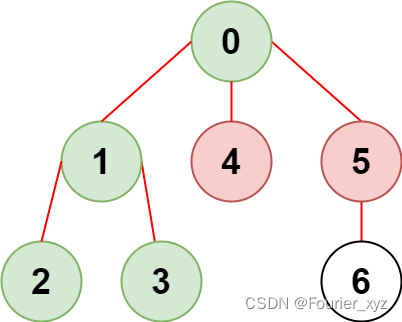
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

解：
根据自己理解撸出来的简易并查集：

class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
        # 个人实现的简单并查集
        node_cnt = 0
        disjoint_set = list(range(n))
        restricted_map = {}
        for i in restricted: restricted_map[i] = True
        for i,j in edges:
            if(i in restricted_map or j in restricted_map): continue
            self.merge(disjoint_set,i,j)

        root = self.find(disjoint_set,0)
        for i in range(n):
            if(self.find(disjoint_set,i) == root): node_cnt += 1
        # print(disjoint_set)
        return node_cnt

    def merge(self,disjoint_set,i,j):
        root_i = self.find(disjoint_set,i)
        root_j = self.find(disjoint_set,j)
        # 暴力合树
        if(root_j != root_i):
            disjoint_set[root_i] = root_j

    def find(self,disjoint_set,i):
        if(disjoint_set[i] != i):
            disjoint_set[i] = self.find(disjoint_set,disjoint_set[i])
        return disjoint_set[i]