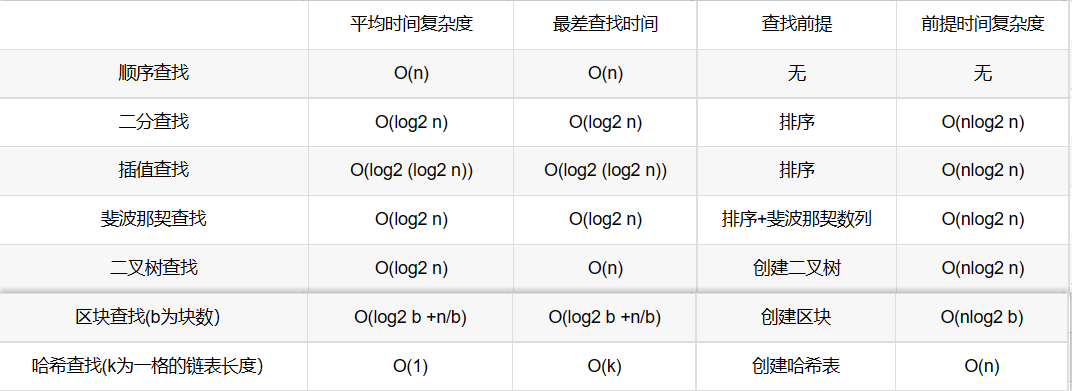
顺序查找(顺序表查找)
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结 点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
private static int sequenceSearch(int[] nums, int target) {
for(int index=0;index<nums.length;index++){
if (nums[index]==target) return index;
}
return -1;
}时间复杂度为O(n)
折半查找(有序查找)
折半查找(Binary Search)技术,又称为二分查找。它的前提是线性表中的记录必须是关键码有序(通常从小到大有序) ,线性表必须采用顺序存储。折半查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
非递归算法:
private static int binarySearch1(int[] sortnums, int target) {
int left=0;
int right=sortnums.length-1;
while(left<=right){
int mid =(left+right)/2;
if (target==sortnums[mid]) return mid;
if(target < sortnums[mid]) right=mid-1;
if (target > sortnums[mid]) left=mid+1;
}
return -1;
}递归算法:
private static int binarySearch2(int[] sortnums, int target,int left,int right) {
if (left <= right){
int mid=(left+right)/2;
if(target==sortnums[mid]) return mid;
if(target<sortnums[mid]) return binarySearch2(sortnums,target,left,mid+1);
if (target>sortnums[mid]) return binarySearch2(sortnums,target,mid+1,right);
}
return -1;
}时间复杂度为O(logn)
插值查找(有序查找)
插值查找是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的 查找方法,其核心就在于插值的计算公式。
简而言之,基于二分查找算法,将查找点的选择改进为自适应选择。
非递归方法:
private static int insertSearch1(int[] sortnums, int target) {
int left=0;
int right=sortnums.length-1;
while(left<=right){
int mid =left+((target-sortnums[left])/(sortnums[right]-sortnums[left]))*(right-left);
if (target==sortnums[mid]) return mid;
if(target < sortnums[mid]) right=mid-1;
if (target > sortnums[mid]) left=mid+1;
}
return -1;
}递归算法:
private static int insertSearch2(int[] sortnums, int target, int left, int right) {
if (left <= right){
int mid=left+((target-sortnums[left])/(sortnums[right]-sortnums[left]))*(right-left);
if(target==sortnums[mid]) return mid;
if(target<sortnums[mid]) return binarySearch2(sortnums,target,left,mid+1);
if (target>sortnums[mid]) return binarySearch2(sortnums,target,mid+1,right);
}
return -1;
}查找成功或者失败的时间复杂度均为O(log2 (log2 n))
斐波那契查找(有序)
与二分法、插值排序方法类似,只是关于mid的确定与斐波那契数列有关。
在斐波那契数列中的元素满足这样的关系:F[k]=F[k-1]+F[k-2],此处将这个数组稍微改一下,改成:(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1

开始表中记录的个数为某个斐波那契数小1,及len=Fib(k)-1.
斐波那契数列中的数值都是固定的,但要查找的数组的长度不固定,此时需要的是创建新数组,使新数组的长度是斐波那契数列中的值,并且是比原数组长度略大的值,多出来的元素用原数组最高位元素补充
斐波那契查找算法
1 ) 当 key=nums[mid] 时,查找就成功。
2 ) 当 key<nums[mid]时,新范围是第low个到第mid-1个,此时范围个数为f[k-1]-1个;
3 ) 当 key>nums[mid]时,新范围是第mid+1个到第high个,此时范围个数为f[k-2]-1个。
private static int fibonacciSearch(int[] nums, int target) {
int len=nums.length;
//构建特殊的Fibonacci数组,
ArrayList<Integer> fibo = new ArrayList<Integer>();
fibo.add(1);
fibo.add(1);
int k=2;
while (true){
int num=fibo.get(k-1)+fibo.get(k-2);
fibo.add(num);
if (fibo.get(k)-1>len) break;
k++;
}
//斐波那契数列的最符合略大于原数组的Fibonacci数f(k)
int[]temp = Arrays.copyOf(nums,fibo.get(k));
for (int i=len+1;i<fibo.get(k);i++){
temp[i]=nums[len-1];
}
int start=0;
int end=len-1;
while (start<=end){
int mid=start+fibo.get(k-1)-1;
if (target==nums[mid]) return mid;
if (target>nums[mid]) {
start=mid+1;
k--;
}
if (target<nums[mid]){
end=mid-1;
k-=2;
}
}
return -1;
}二叉排序树查询
二叉排序树的性质:
- 若左子树不空,则左子树上所有结点的键值均小于或等于它的根结点的键值。
- 若右子树不空,则右子树上所有结点的键值均大于或等于它的根结点的键值。
- 左、右子树也分别为二叉排序树。
二叉排序树的创建:
private static void CreateShu(){
int[] array = {35,76,6,22,16,49,49,98,46,9,40};
BinaryTree root = new BinaryTree(array[0]);
for(int i = 1; i < array.length; i++){
createBST(root, array[i]);
}
}
public static void createBST(BinaryTree root, int element){
BinaryTree newNode = new BinaryTree(element);
if(element > root.value){
if(root.right == null)
root.right = newNode;
else
createBST(root.right, element);
}else if(element < root.value){
if(root.left == null)
root.left = newNode;
else
createBST(root.left, element);
}else{
System.out.println("该节点" + element + "已存在");
return;
}
}二叉排序树的查找:
基本思想:
与节点进行比较,等于节点的值则查找成功
大于节点的值则遍历查找节点的左孩子
小于节点的值则遍历查找节点的右孩子
public static void searchBST(BinaryTree root, int target, BinaryTree p){
if(root == null){
System.out.println("查找"+target+"失败");
}else if(root.value == target){
System.out.println("查找"+target+"成功");
}else if(root.value >= target){
searchBST(root.left, target, root);
}else{
searchBST(root.right, target, root);
}
}分块查找
分块查找的基本思想:将查找表分为若干子块。块内的元素可以无序,但块之间是有序的,即第一个块中的最大关键字小于第二个块中的所有记录的关键字,第二个块中的最大关键字小于第三个块中的所有记录的关键字,以此类推。再建立一个索引表,索引表中的每个元素含有各块的最大关键字和各块中的第一个元素的地址,索引表按关键字有序排列。
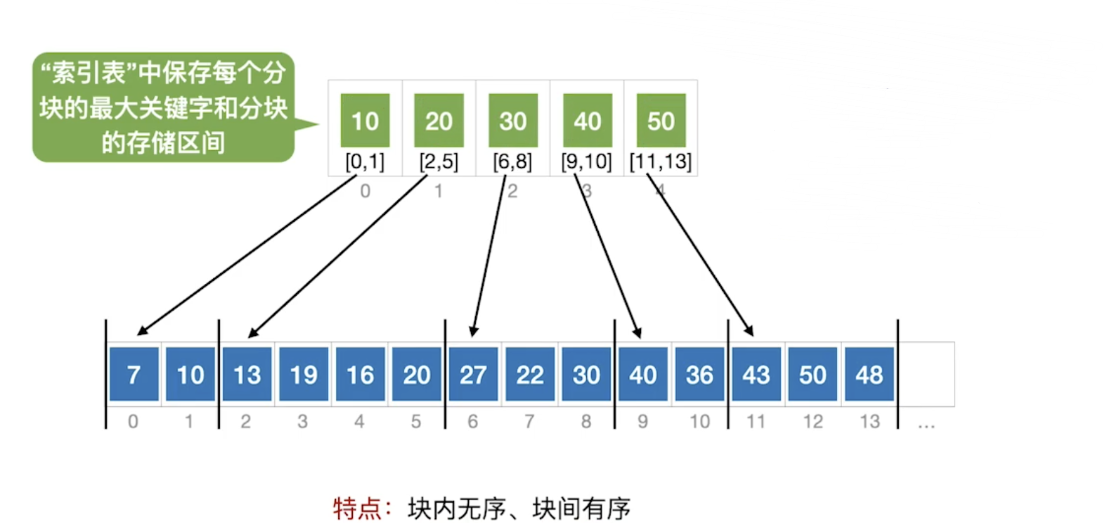
以查找36为例
1.在索引表中依次遍历找到第一个大于它的值,即40
2.移动到40指向的数组区间的第一个元素,即数组下标9
3.从数组下标9开始遍历,40→36 找到36
哈希表查找
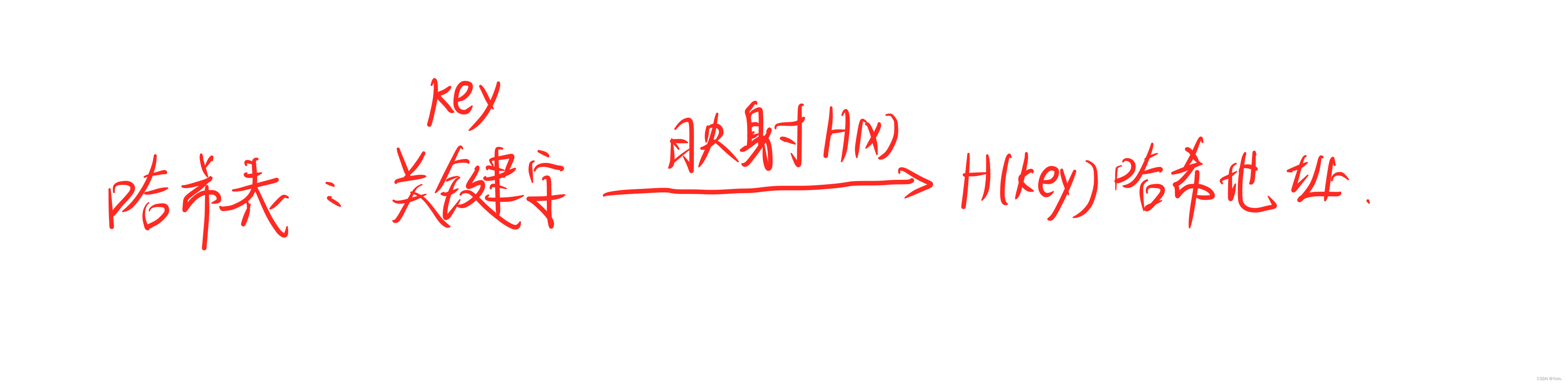
哈希表则通过计算一个以记录的关键词为自变量的函数(哈希函数H(x))来得到该机里的存储地址,所以在哈希表中进行查找操作时,需要同一哈希函数计算得到待查记录的存储地址,然后到相应的存储单元去获得有关信息在判定查找是否成功。
通过哈希函数H(key)和处理冲突的方法,将一组关键字映射,形成哈希散列。
对于某个哈希函数H和两个关键字
和
,如果
,而H(
)=H(
),则称为冲突。具有相同的哈希函数值的关键字对该哈希函数成为同义词。
哈希函数的构造
- 常见的哈希函数构造方法
直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法
- 处理冲突的方法
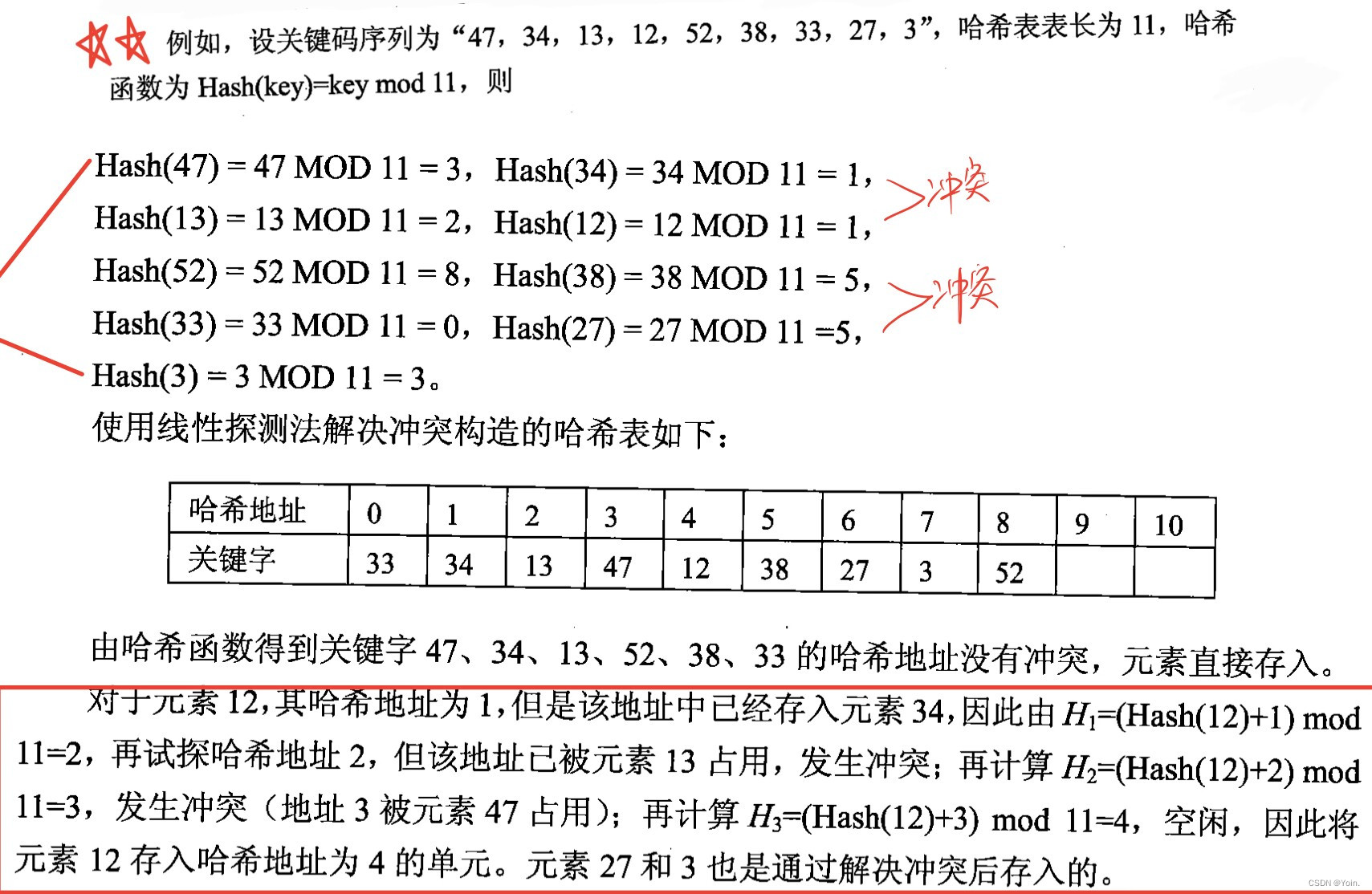
(1)开放定址法

线性探测法可能使第i个哈希地址的同义词存入第i+1个哈希地址,这样本应存入第i+1个哈希地址的元素变成第i+2个哈希地址元素的同义词。
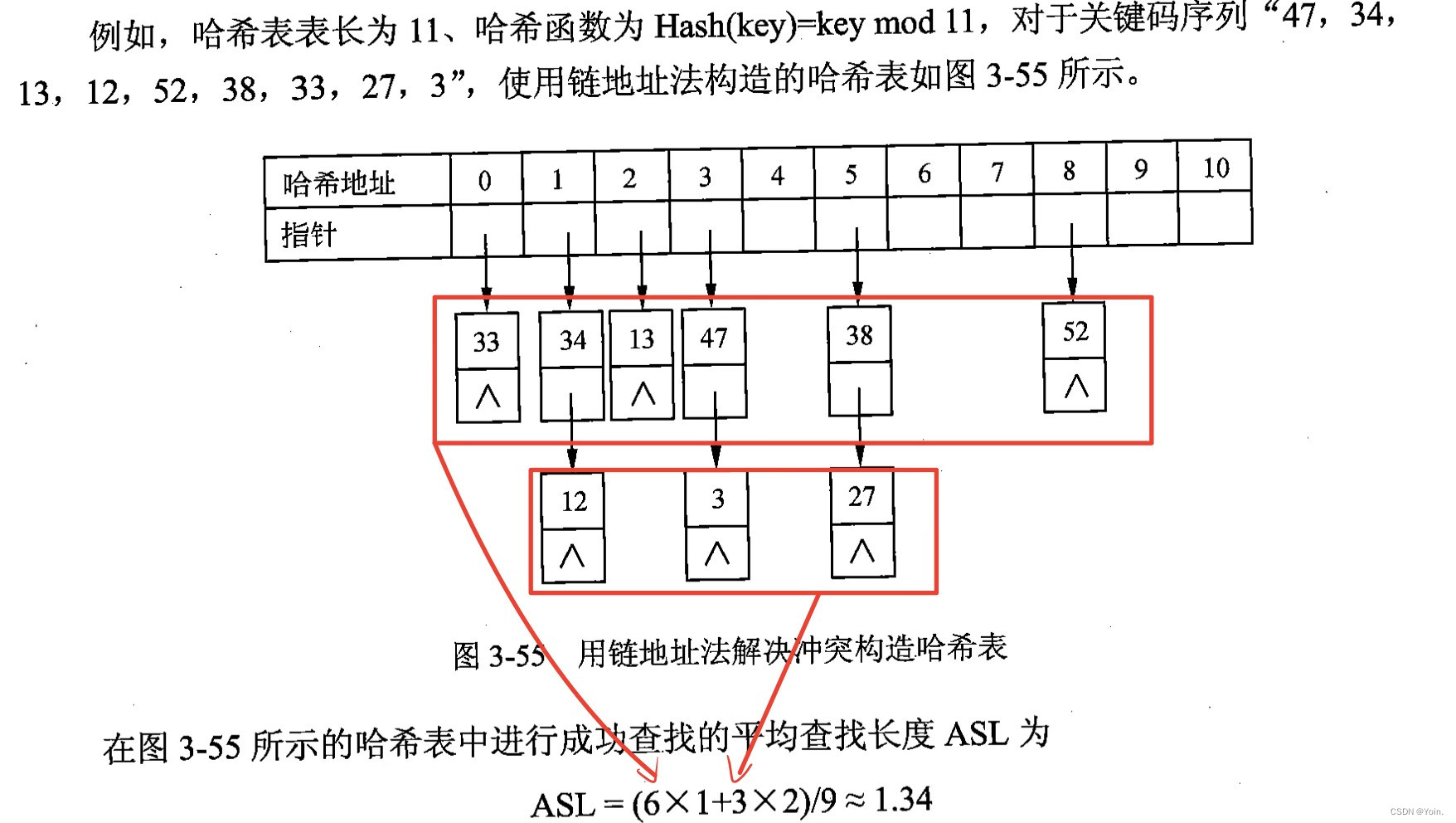
(2)链地址法:查找表的每一个记录中增加一个链域,链域中存放下一个具有相同哈希函数值的记录的存储地址(对于发生冲突时的查找和插入操作就跟线性表一样)。
(3)再哈希法:RHi均是不同的哈希函数,即在同一词发生地址冲突时计算另一个哈希函数地址,直到冲突不再发生。
哈希函数的装填因子:α标志着哈希表的装满程度,α越小,发生冲突的可能性越小。
表中装入的记录数 / 哈希表的长度
算法思想:key-value存储思想,key存值,value存索引
private static int hashSearch(int[] nums, int target) {
HashMap<Integer,Integer> hashNums = new HashMap<Integer,Integer>();
for (int i=0; i<nums.length; i++){
hashNums.put(nums[i],i);
}
if (hashNums.get(target) !=null) return hashNums.get(target);
return -1;
}哈希表的构造方法:
1、直接定址法
哈希地址:f(key) = a*key+b (a、b为常数)。
2、数字分析法
假设关键字是R进制数(如十进制)。并且哈希表中可能出现的关键字都是事先知道的,则可选取关键字的若干数位组成哈希地址。选取的原则是使得到的哈希地址尽量避免冲突,即所选数位上的数字尽可能是随机的。
3、平方取中法
取key平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,仅取其中的几位为地址不一定合适。而一个数平方后的中间几位数和数的每一位都相关, 由此得到的哈希地址随机性更大。如key是1234,那么它的平方就是1522756,再抽取中间的3位就是227作为 f(key) 。
4、折叠法
折叠法是将 key 从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些),然后将这几部分叠加求和,并按哈希表的表长,取后几位作为 f(key) 。
比如key是9876543210,哈希表的表长为3位,我们将 key 分为4组,987 | 654 | 321 | 0 ,然后将它们叠加求和 987+654+321+0=1962,再取后3位即得到哈希位置是:962 。
5、除留余数法
取关键字被某个不大于哈希表表长 m 的数 p 除后所得的余数为哈希地址。即 f(key) = key % p (p ≤ m)。这种方法是最常用的哈希函数构造方法。
6、随机数法
哈希地址:random(key) ,这里random是随机函数,当 key 的长度不等时,采用这种方法比较合适。
查找总结: