---

一、优先级队列的概念

队列是一种先进先出(FIFO)的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列
在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)
PriorityQueue底层使用了堆这种数据结构，而堆实际就是在完全二叉树的基础上进行了一些调整

二、优先级队列的模拟实现

1.堆的存储

堆的性质：
(1).堆中某个节点的值总是不大于或不小于其父节点的值；
(2).堆总是一棵完全二叉树
堆的存储方式有：小根堆、大根堆
小根堆：根节点总是比左右子节点小

大根堆：根节点总是比左右子节点大

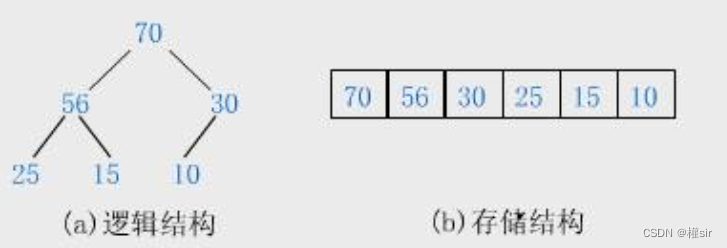
堆是一棵完全二叉树，因此可以用层序存储的方式进行，存储在数组当中
将元素存储到数组后，在以实现树的方式对堆进行实现。设 i 结点为数组中的下标，则有以下特点：
(1).如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
(2).如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子
(3).如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

2.堆的创建

这里我们创建的堆是大根堆的形式
大根堆的特点是根节点的元素始终比左右子树都要大，所以我们要调整这棵树，是需要将较小的根的从上面下降至下面，简称向下调整。这里，就需要定义两个变量，一个找到最后一个数组元素即 child 结点，另一个则要找到这个结点的父节点即 parent 结点
我们以集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据，将其创建成大根堆

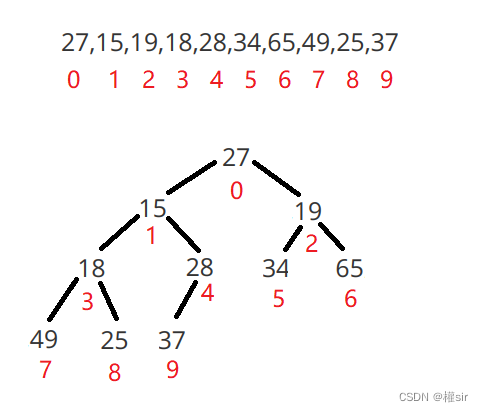
大致操作如下图，以 第一次调整 数字 37 为例实现：

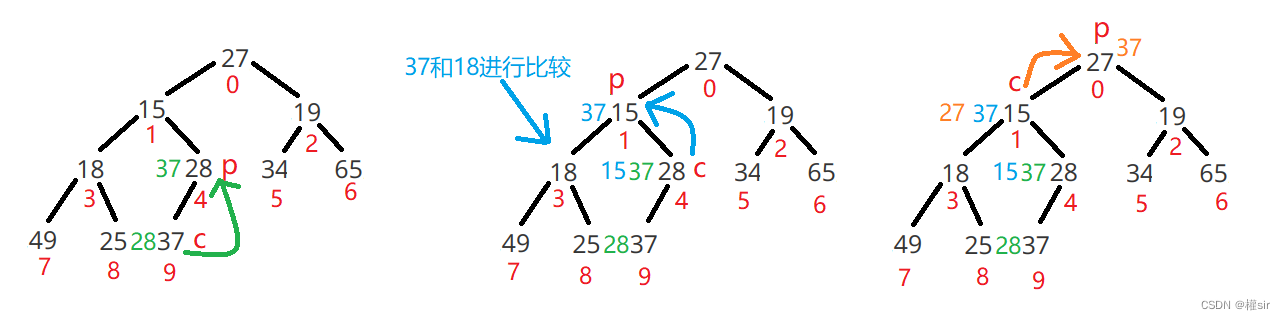
3.代码的实现

public class TestHeap {
    public int[] elem;
    public int usedSize;
    //对数组进行初始化
    public TestHeap() {
        this.elem = new int[10];
    }
    //赋值
    public void initElem(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }
    //创建堆
    public void createBigHeap() {
        for (int parent = (usedSize-1-1)/2; parent >=0 ; parent--) {
            //向下调整
           siftDown(parent,usedSize);
        }
    }
    private void siftDown(int parent,int end) {
        //孩子结点
        int child = 2*parent+1;
        while (child < end) {
            //前一个判断防止越界，后一个判断找左右孩子的最大值
            if(child+1 < end && elem[child] < elem[child+1]) {
                child++;
            }
            //找到最大值之后与parent进行比较并交换
            if(elem[child] > elem[parent]) {
                swap(parent,child);
                //交换之后还要保证下面的树也是大根堆
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }
    private void swap(int i,int j) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }
}

以下是大根堆创建完成的结果：

插入操作：
在进行插入操作时我们要考虑以下几个问题：
(1).在插入元素时我们要注意数组是否已经满了
(2).插入元素的位置是插入在数组的末尾，即树的最后一个结点
(3).插入的元素要进行向上移动的操作

    public void offer(int val) {
        //判断数组是否满了，满了就进行扩容
        if(isFull()) {
            this.elem = Arrays.copyOf(elem,2*elem.length);
        }
        //在末尾插入元素
        elem[usedSize] = val;
        usedSize++;
        //进行向上调整
        siftUp(usedSize-1);
    }
    public void siftUp(int child) {
        //要插入结点的父亲结点 
        int pareat = (child-1)/2;
        while (child > 0) {
            if(elem[child] > elem[pareat]) {
                swap(child,pareat);
                child = pareat;
                pareat = (child-1)/2;
            }else {
                break;
            }
        }
    }
    public boolean isFull() {
        return usedSize == elem.length;
    }

删除操作：
删除元素要注意：
删除的是堆顶的元素，将第一个元素与最后一个元素进行交换，然后向下调整

    public int poll() {
        //把要删除的结点和最后一个结点进行交换
        int tmp = elem[0];
        swap(0,usedSize-1);
        usedSize--;
        //对交换后的元素进行向下调整
        siftDown(0,usedSize);
        return tmp;
    }