2368. 受限条件下可到达节点的数目

题目描述：

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

示例 1：

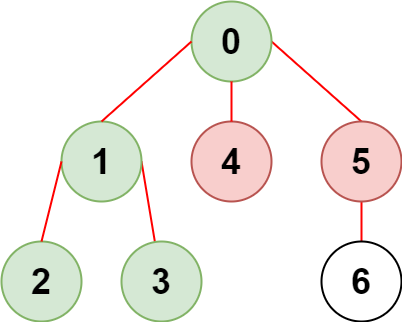
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

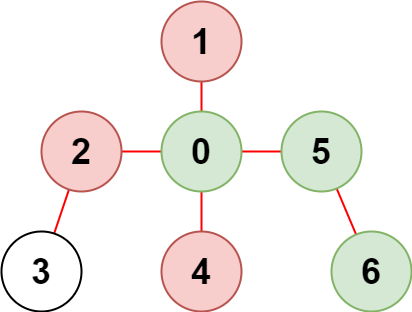
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

• 2 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= a_i, b_i < n
• a_i != b_i
• edges 表示一棵有效的树
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted 中的所有值 互不相同

思路：

用布尔数组记录哪些节点是受限的。

然后建树，只有当两个节点都不是受限的（都不在哈希集合中）才连边。

从 0出发 DFS 这棵树，统计能访问到的节点个数，即为答案

代码：

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        //有节点的长度n
        boolean[]visit=new boolean[n];//用来描述是否受限
        for(int x:restricted){
            visit[x] = true;//受限则标记
        }
        List<Integer>[] g =new ArrayList[n];//初始化邻接表
        Arrays.setAll(g,i -> new ArrayList<>());//列表每个位置都保存一个数组
        for(int[] e:edges){
            int x=e[0],y=e[1];
            if(!visit[x] && !visit[y]){
                g[x].add(y);//均不受限链接表
                g[y].add(x);
            }
        }
        return dfs(0,-1,g);//从0根节点开始遍历
    }
    private int dfs(int x,int fa, List<Integer>[] g){
        //统计访问x节点时可访问的节点数
        int cnt = 1;
        for(int y :g[x]){
            if(y!=fa){
                cnt+=dfs(y,x,g);
            }
        }
        return cnt;
    }

}