现在我们已经对模型训练有了初步了解，下面我们接着聊评估：

一. 回归模型的性能评估

对于一个已经训练好的回归模型，我们需要知道模型训练的好坏程度，即需要对模型进行评估

这里给出几个评估指标：

1. 平均平方误差(MSE)

$$MSE=\frac{1}{m}\sum _{i=1}^m(y_i-{\hat{y}}_i{)}^2，又称为均方误差$$

2. 平均绝对误差(MAE)

$$MAE=\frac{1}{m}\sum _{i=1}^m\mid y_i-{\hat{y}}_i\mid ，又称为绝对误差$$

3. $R^2$ 值

默认LinearRegression.score( ) 的评分为$R^2$ 值

$$R^2=1-\frac{RSS}{TSS}=1-\frac{{\sum }_{i=1}^m(y_i-{\hat{y}}_i{)}^2}{(y_i-\bar{y}{)}^2}，其中\bar{y}=\frac{1}{m}\sum _{i=1}^m{y}_i$$

其中$r^2$的取值范围为(-∞,1]

	当值为1时，即 预测值 = 真值
	当值为0时，即 预测值 = 均值 （预测结果很差）
	当值小于0时，模型一定有问题，不如直接用均值

3.1 $R^2$优点

	给定指标范围，对于模型好坏的判断会更直观

二. 分类模型的性能评估

这里我们先引入混淆矩阵

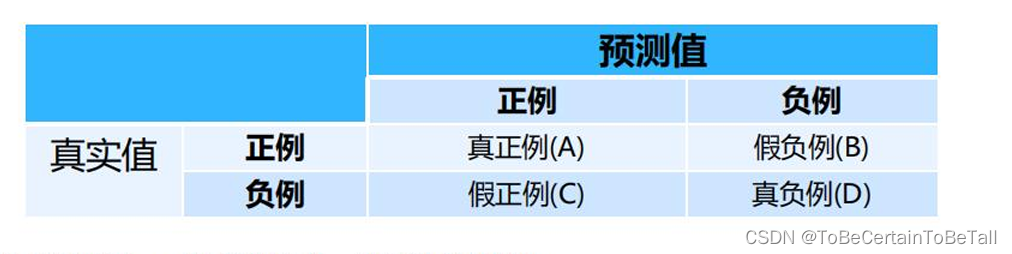
	概念解释：
		混淆矩阵是在统计学中用来衡量分类模型性能的矩阵
		它以矩阵的形式展示了模型在测试数据集上的预测结果与实际结果之间的关系

这里补充什么是正例：工程中关注的为正例，取决于需求；比如，核酸的阳性，垃圾邮件等都可以为正例

1. 准确率（Accuracy）

$$Accuracy=\frac{A+D}{A+B+C+D}$$

	检测正确的样本数/总样本数
	
	注意：一般不用这个指标
	原因：在正负样本数差距太大时，会失真
	比如：
		阴性样本990个，阳性样本10个
		模型检测到了所有得阴性样本，即990个
		模型此时准确率为99%

2. 召回率（Recall）

$$Recall=\frac{A}{A+B}$$

	检测正确的正例样本数/总正例样本数

3. 精确率（Precision）

$$Precision=\frac{A}{A+C}$$

	检测正确的正例样本数/检测为正例的样本数

---

	召回率和精确率，谁更重要？
		看工作需求，以及后续操作
	
	对于这两个指标，再补充一种好理解得方式：
		召回率：是目标就揪出来
		精确率：目的地必须是目标
			例子：
				正常邮件必须放在A内，不能出现在垃圾邮件存放处
				垃圾邮件偶尔可以出现在A处
				垃圾邮件存放处只能存放垃圾邮件

4. $F_{Score}$

精确率和召回率互相影响，理想状态下肯定追求两个都高
但是实际情况是两者相互“制约”：
追求精确率高，则召回率就低
追求召回率高，则通常会影响精确率

分类模型默认的评估指标

$$F_{Score}=(1+{\beta }^2)\frac{Precision\ast Recall}{{\beta }^{2}Precision+Recall}$$

	 β=1：表示Precision与Recall一样重要
	 	F1可以看作是模型准确率和召回率的调和平均数，最大值是1，最小值是0
	 	注意：存在精确率和召回率都为1时
	 β<1：表示Precision比Recall重要
	 β>1：表示Recall比Precision重要

5. PR-曲线和AP值

	以召回率为横轴，精确率为纵轴，即画出PR-曲线
	PR曲线与X轴围成的图形面积，即AP值
		AP值为1时模型性能最好

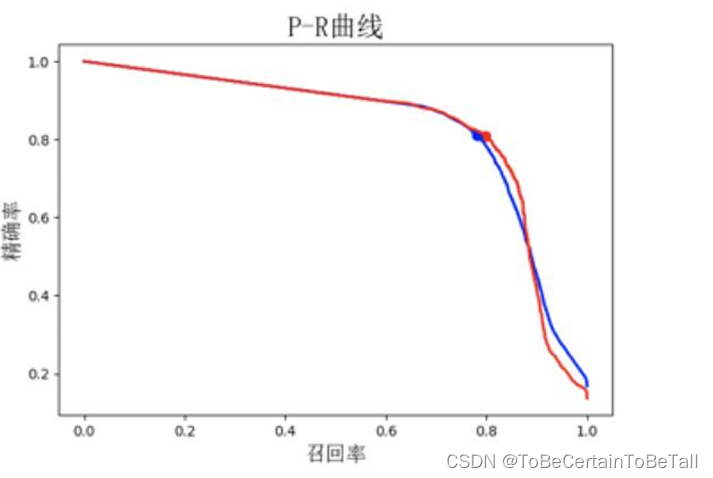
	PR曲线由阈值控制
	比如：
		0.3以上全部判为阳性
			抓回的样本数量多，即召回率高
			抓回样本中有阴性样本，即精确率低
			
	即随着阈值的降低，召回率越高，精确率越低
	比如：
		AP值小，即面积较小时，说明：P值下降很快，阈值在0.7左右时有大量负样本

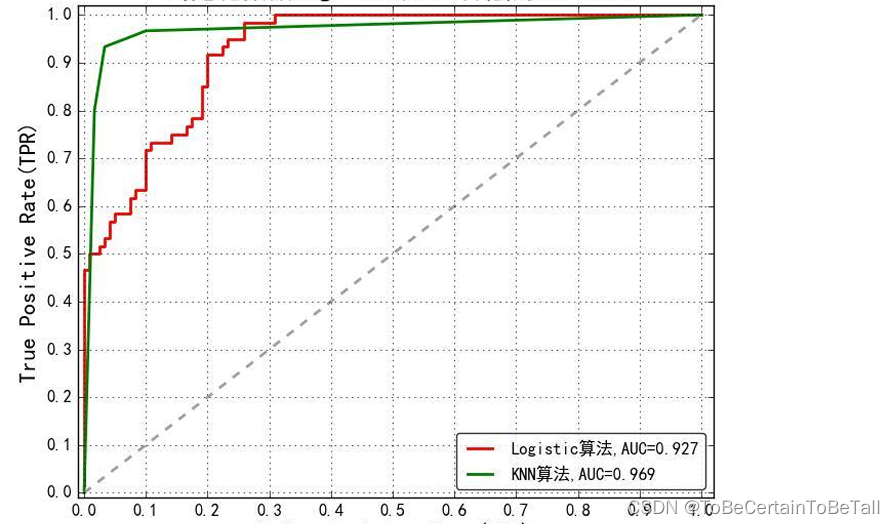
6. ROC曲线

	横坐标为false positive rate(FPR)：FP/(FP+TN)
	纵坐标为true positive rate(TPR)：TP/(TP+FN)

分类器有概率输出，50%常被作为阈值点，可以调节阈值，改变预测的标签

当阈值取0时，对应图中的右上角点(全部预测为正例)
当阈值取1时，对应图中的左下角点(全部预测为负例)
 
ROC曲线越接近左上角(0,1)，该分类器的性能越好

ROC曲线反映了FPR与TPR之间权衡的情况，即

在TPR随着FPR递增的情况下，谁增长得更快，快多少的问题

	模型分类性能越好：
	TPR增长得越快，曲线越往上屈，AUC就越大
		
		其中，AUC为ROC曲线下的面积，取值范围是[0.5,1]