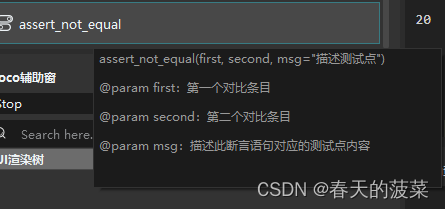
1.为了较为清晰的写出各种情况,接下来的代码中不会出现else,而是将每一个else if均给写出来!!!
2.为了防止每次的mid溢出,我们均写为mid = left + (right - left)
基本的二分查找模板(寻找一个数)
基本问题描述:在一组数中能否找到一个目标数target,若找到则返回其索引,找不到则返回-1;
代码:
/**
* Basic binary search template
*
* @param nums Given array
* @param target Given target number
* @return int
*/
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left);
//Have found
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
}
}
return -1;
}
具体细节分析可参考另一篇文章:
二分查找中的部分细节与模版1(附带力扣题目)
寻找左、右侧边界的二分查找模板
新问题的提出
现在给你一个数组nums = [[1,2,2,2,3];和一个目标值target = 2,假如现在要求还是使用二分查找对数级的时间复杂度来找出target左、右则边界;该如何实现?
由上述问题我们可以引出寻求左、右边界二分查找模板
寻找左侧边界的二分查找模板
/**
* Find a set of numbers that are smaller than target
*
* @param nums Given array
* @param target Given target number
* @return int
*/
int left_bound(int[] nums, int target) {
if (nums.length == 0) {
return -1;
}
int left = 0;
int right = nums.length;//Look out
while (left < right) { //Look out
int mid = left + (right - left);
//Have found
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] > target) {
right = mid;//Look out
} else if (nums[mid] < target) {
left = mid + 1;
}
}
return left;
}
寻找左侧边界模板的细节解释
1.为什么while中此时是 **<**而不是 <=;
因为此时right = nums.length,则表示的搜索区间是**[left, right)左闭右开**;则while (left < right) 的终止条件是left == right,此时的搜索区间**[left, right)**为空,即可以正确终止。
2.如果nums中不存在target该返回什么?(代码中没有返回**-1**的操作)
请读者先按上述代码手动模拟给定nums为[1,2,2,2,3]、[2,3,5,7]、[2,3,5,7],target分别对应为2,1,8时代码会返回什么(答案分别是:1,0,4);
对此我们对这段代码的理解是对于给定数组nums中存在多少个数小于target!!!;
综上函数返回值left的取值范围为[0, left.length];所以添加两行代码就能在正确的时候return -1;
//target is larger than all the numbers
if (taeget == nums.length) {
return -1;
}
return nums[left] == target ? left : -1;
3.为什么是left = mid + 1; right = mid;
由于此时我们的搜索区间为**[left, right)左闭右开**,所以当nums[mid]被检测完后下一步就是去掉mid分割为两个区间,即**[left mid) [mid + 1, right) 两个区间也均是左闭右开的**
4.为什么该算法能够搜索左侧边界?
关键在于**nums[mid] == target时right = mid;**即找到target时不是立即返回,而是缩小搜索区间,达到锁定左侧边界的目的。
5.为什么返回left而不是right?
因为此时循环退出条件时left == right,所以返回left还是right都是一样的!!!
寻找左边界模板的另一种写法(与基本模板对齐)
为了使得改模板在形式上尽量和基本模板对其(方便我们的记忆),我们先要做如下改写:
1.right = nums.length - 1;此时搜索区间就是全闭的
2.由于此时搜索区间是全闭的所以循环的终止条件就是left == right + 1;所以此时while循环的退出条件是left <= right;
3.由于此时搜索区间是全闭的,所以在去除mid后余下的两个区间也应该是全闭的则**[left, mid - 1] 、[mid + 1, right]**
则此时我们可以初步写出大致的代码:
int left_bound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
但是此时我们注意到由于while退出条件是left == right + 1,所以当target比nums中的所有元素都大时,则会存在索引越界的情款!!!
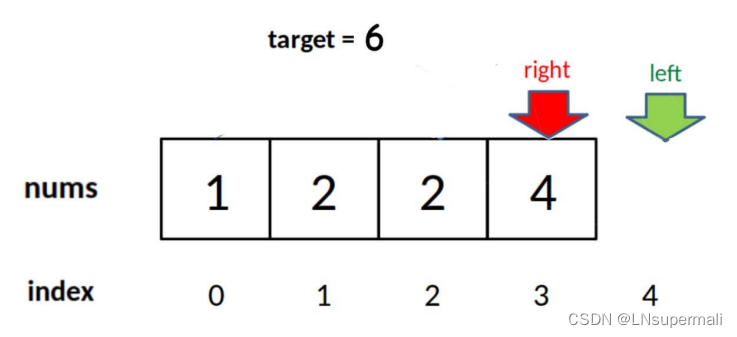
则要添加上一段检测索引越界情况的代码:
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
则最终的完整代码模板是:
/**
* Look for the left boundary template
*
* @param nums Given array
* @param target Given target number
* @return int
*/
int left_bound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
}
}
寻找右侧边界二分查找模板
左闭右开写法:
/**
* Look for the right boundary template
*
* @param nums Given array
* @param target Given target number
* @return int
*/
int right_bound(int[] nums, int target) {
int left = 0;
int right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
} else if (nums[mid] == target) {
right = mid + 1;
}
}
return left - 1;
}
寻找右侧边界二分查找模板的细节解释
1.为什么可以找到右侧边界
关键在于if(nums[mid] == target) left = mid + 1;是不断在增大搜索区间的下界left使得区间不断向右收缩,达到锁定右侧边界的目的.
2.为什么最终返回left-1?
因为我们对 left 的更新必须是 left = mid + 1 ,就是说 while 循环结束时, nums[left] ⼀定不等于 target 了,⽽ nums[left-1] 可能是target 。
3.为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
类似之前的左侧边界搜索,因为 while 的终⽌条件是 left == right ,就是说 left 的取值范围是 [0, nums.length] ,所以可以添加两⾏代码,正确地返回 -1:
while (left < right) {
}
if (left == 0) {
return -1;
}
return nums[left - 1] == target ? (left - 1) : -1;
寻找右侧边界二分查找模板的另一种写法(对齐基本二分查找模式)
/**
* Look for the right boundary template
*
* @param nums Given array
* @param target Given target number
* @return int
*/
int right_bound(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
//Contracted left boundary
left = mid + 1;
}
}
// Instead, check the right out of bounds.
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}
当target比所有元素小时,right会被减到-1,所以最后要防止越界.
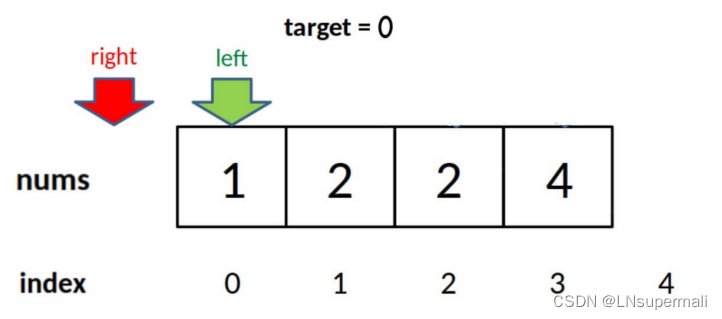
力扣题目(35. 搜索插入位置)
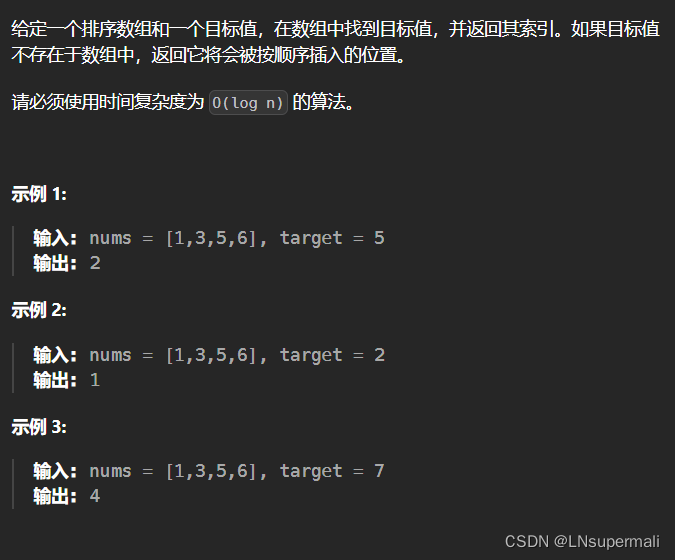
题目描述:
解题思路:
由于当target大于nums中的所有数时,直接放置于nums[nums.length - 1];当target小于nums中的所有数时,直接放置于nums[0];其它情况时则等价求取给定数组中小于给定值target的个数有多少个,则直接套用前面寻找左侧边界模板
代码:
class Solution {
public:
/**
* Binary search
*
* @param nums Given array
* @param target Given number
* @return int
*/
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
return left;
}
};