【快速选择】解决TopK问题

news2024/11/17 16:26:14

目录

一、什么是TopK问题

二、优先级队列

优先级队列介绍

代码实现

三、使用优先级队列解决TopK问题

四、快速选择算法解决TopK问题

快速选择

图解快速选择

代码解决前k小个元素

五、优先级队列与快速选则算法比较

优先级队列

快速选择

一、什么是TopK问题

TopK问题就是在一个数组中寻找出最小（大）的前K个数，或者寻找出第K大（小）的数

常见TopK问题图示

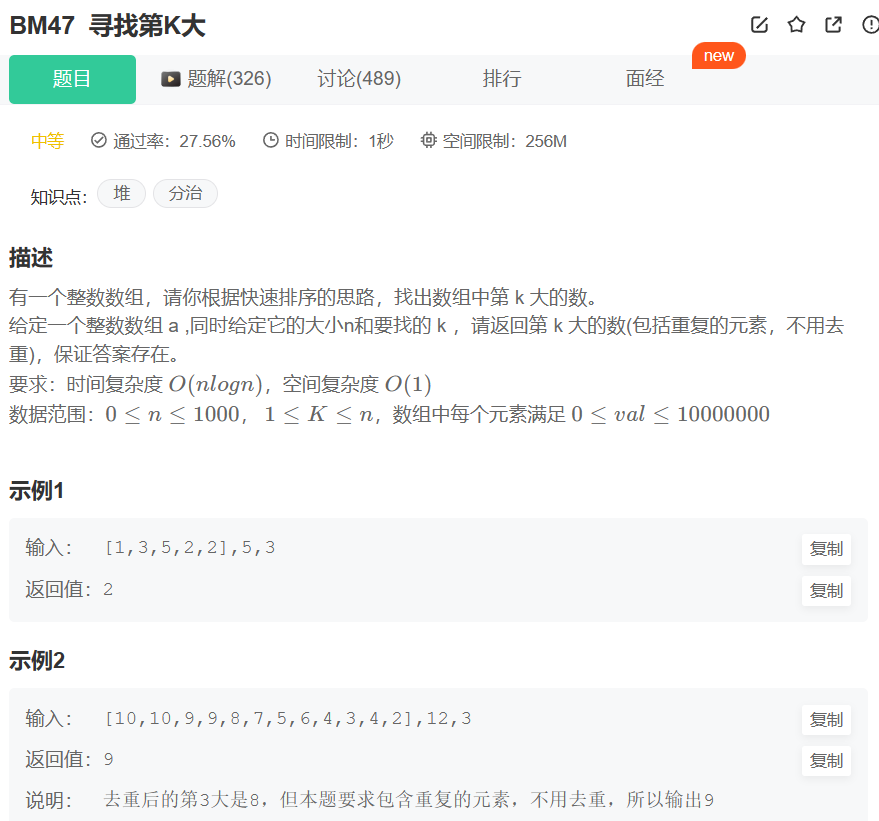
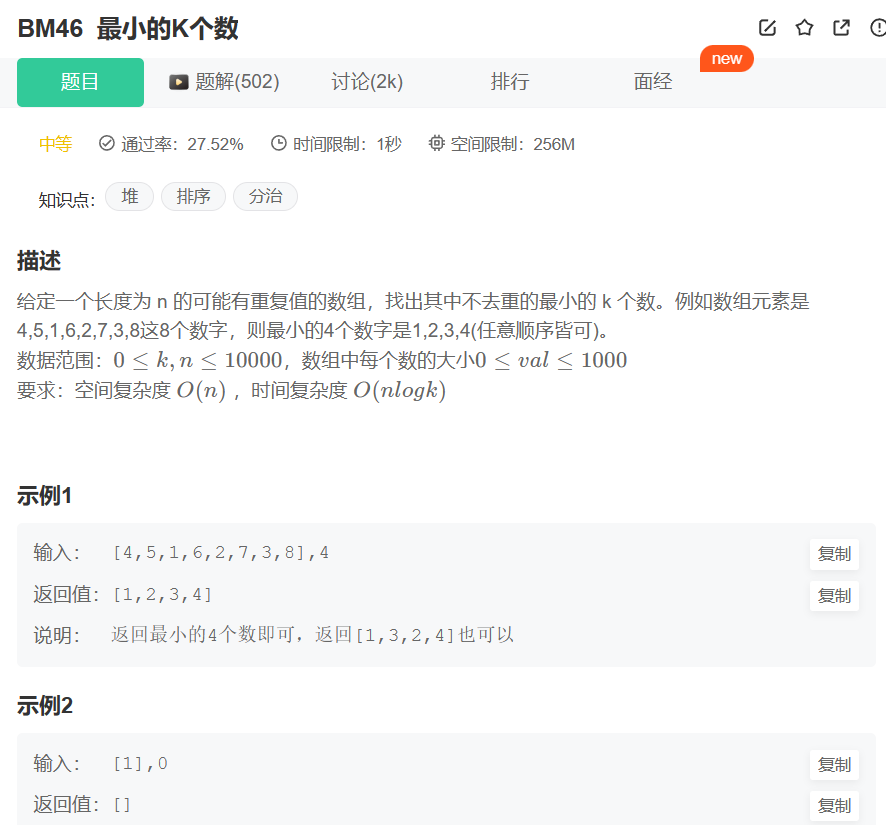
常见TopK问题链接

最小的K个数_牛客题霸_牛客网给定一个长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数。例如数组元素是。题目来自【牛客题霸】icon-default.png?t=N7T8https://www.nowcoder.com/practice/6a296eb82cf844ca8539b57c23e6e9bf?tpId=295&tqId=23263&ru=/exam/oj&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Foj

寻找第K大_牛客题霸_牛客网

. - 力扣（LeetCode）

二、优先级队列

优先级队列介绍

优先级队列是一种数据结构，它根据元素的优先级来决定元素的插入和删除顺序。以下是一些关键特点：

  1. 基于优先级排序：每个元素在队列中都有一个优先级，优先级最高的元素会首先被移除。
  2. 使用特定数据结构：优先级队列通常可以使用堆（尤其是二叉堆）这种数据结构来实现，以保持队列的有序状态并高效地处理插入和删除操作。
  3. 应用广泛：它在很多算法中有广泛应用，如任务调度、最短路径寻找、事件驱动模拟等场合。
  4. 自定义比较：可以通过仿函数或运算符重载来支持自定义的数据类型和比较函数，从而定义元素的优先级。
  5. Java实现：在Java中，优先级队列可以通过最小堆来实现，其中的元素按照自然顺序或者根据提供的Comparator来确定优先级。
  6. 操作方法：主要操作包括插入元素（入队）和删除最高优先级的元素（出队）。
  7. 性能优化：由于内部结构的优化，即使在大量元素的情况下，优先级队列依然能够快速地确定下一个要处理的元素。

总的来说，优先级队列提供了一种有效的方式来管理那些需要按照特定顺序处理的元素，是许多复杂算法和系统设计中不可或缺的工具。

优先级队列博客

【数据结构】优先级队列（堆）与PriorityQueue_unsortedpriorityqueue增加复杂度为1的getmax-CSDN博客文章浏览阅读504次，点赞2次，收藏2次。比如一组数据 1 2 3 4 5 6，我们将他创建成一个大根堆时，我们先从最后一个位置所在的树开始进行调整，由于我们能获取到数组的长度，且根据堆的性质父亲节点的下标 * 2 + 1就孩子节点下标可知，知道孩子的下标（数组长度-1）就能知道父亲的下标。比如我们在大根堆 4 3 2 2 1 1的堆里插入11，先将11存在最后，然后拿他与父亲比较，如果大就交换，如果不比父亲大那他就是大根堆不需要调整，此时交换后，要继续更换父亲与儿子的位置重复比较交换操作，直到孩子下标小于或者等于0时不在需要调整。_unsortedpriorityqueue增加复杂度为1的getmaxhttps://blog.csdn.net/qq_61903414/article/details/128423670?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170929235016777224499491%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=170929235016777224499491&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-128423670-null-null.nonecase&utm_term=%E4%BC%98%E5%85%88%E7%BA%A7%E9%98%9F%E5%88%97&spm=1018.2226.3001.4450

代码实现
import java.util.Arrays;

/**
 * @author 1886
 *
 */
public class PriorityQueue <T extends Comparable<T>> {
    // 优先级队列底层模拟堆的数组
    private Object[] queue;
    // 记录当前优先级队列元素个数
    private int size;

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * 默认构造方法
     */
    public PriorityQueue() {
        this.queue = new Object[DEFAULT_INITIAL_CAPACITY];
    }

    /**
     * 指定大小
     * @param capacity
     */
    public PriorityQueue(int capacity) {
        this.queue = new Object[capacity];
    }

    /**
     * 传入指定数组
     * @param queue
     */
    public PriorityQueue(T[] queue) {
        // 1.初始化成员变量
        this.queue = queue;
        this.size = queue.length;

        // 2.将数组进行大根堆调整
        HeapIfy();
    }
}

/**
 * @author 1886
 *
 */
public class PriorityQueue <T extends Comparable<T>> {
    // 优先级队列底层模拟堆的数组
    private Object[] queue;
    // 记录当前优先级队列元素个数
    private int size;

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * 默认构造方法
     */
    public PriorityQueue() {
        this.queue = new Object[DEFAULT_INITIAL_CAPACITY];
    }

    /**
     * 指定大小
     * @param capacity
     */
    public PriorityQueue(int capacity) {
        this.queue = new Object[capacity];
    }

    /**
     * 传入指定数组
     * @param queue
     */
    public PriorityQueue(T[] queue) {
        // 1.初始化成员变量
        this.queue = queue;
        this.size = queue.length;

        // 2.将数组进行大根堆调整
        heapIfy();
    }

    /**
     * 堆化
     */
    private void heapIfy() {
        for (int parent = (this.size - 1 - 1) >> 1; parent >= 0; parent--) {
            siftDown(parent, this.size);
        }
    }

    /**
     * 向下调整
     * @param parent 父亲节点下标
     * @param len    向下调整的结束位置
     */
    private void siftDown(int parent, int len) {
        // 计算出孩子节点位置
        int child = parent * 2 + 1;
        // 开始向下调整
        while (child < len) {
            // 寻找出两个孩子节点中最大的
            if (child + 1 < len && ((T)queue[child]).compareTo(((T)queue[child + 1])) < 0) {
                child++;
            }

            // 与父亲节点进行判断，如果孩子节点比父亲节点大就进行调整 否则调整完毕
            if (((T)queue[child]).compareTo(((T)queue[parent])) < 0) {
                break;
            } else {
                T tmp = (T)queue[child];
                queue[child] = (T)queue[parent];
                queue[parent] = tmp;

                parent = child;
                child = parent * 2 + 1;
            }
        }
    }
}
import java.util.Arrays;

/**
 * @author 1886
 *
 */
public class PriorityQueue <T extends Comparable<T>> {
    // 优先级队列底层模拟堆的数组
    private Object[] queue;
    // 记录当前优先级队列元素个数
    private int size;

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * 默认构造方法
     */
    public PriorityQueue() {
        this.queue = new Object[DEFAULT_INITIAL_CAPACITY];
    }

    /**
     * 指定大小
     * @param capacity
     */
    public PriorityQueue(int capacity) {
        this.queue = new Object[capacity];
    }

    /**
     * 传入指定数组
     * @param queue
     */
    public PriorityQueue(T[] queue) {
        // 1.初始化成员变量
        this.queue = queue;
        this.size = queue.length;

        // 2.将数组进行大根堆调整
        heapIfy();
    }

    /**
     * 入队操作
     * @param data 进入优先级队列的数据
     */
    public void offer(T data) {
        // 如果优先级队列满 进行扩容
        if (this.size == this.queue.length) {
            grow();
        }

        // 将元素放到末尾
        this.queue[this.size] = data;
        // 进行向上调整
        siftUp(this.size++);
    }

    /**
     * 出队操作
     * @return
     */
    public T poll() {
        // 如果为空就返回空
        if (this.size == 0) return null;

        // 将堆顶元素与最后一个位置进行交换
        T top = (T)queue[0];
        queue[0] = this.queue[this.size - 1];
        queue[this.size - 1] = top;

        // 删除元素
        this.size--;

        // 向下调整
        siftDown(0, this.size);

        // 返回
        return top;
    }

    /**
     * 排序
     */
    public void sort() {
        int len = this.size - 1;
        while (len >= 0) {
            T tt = (T) queue[0];
            queue[0] = queue[len];
            queue[len] = tt;

            siftDown(0, len--);
        }
    }

    /**
     * 堆化
     */
    private void heapIfy() {
        for (int parent = (this.size - 1 - 1) >> 1; parent >= 0; parent--) {
            siftDown(parent, this.size);
        }
    }

    /**
     * 向上调整
     * @param child
     */
    private void siftUp(int child) {
        // 计算出父亲节点的下标
        int parent = (child - 1) / 2;
        // 开始向上调整
        while (child > 0) {
            if (((T)queue[child]).compareTo((T)queue[parent]) >= 0) {
                T tmp = (T)queue[child];
                queue[child] = (T)queue[parent];
                queue[parent] = tmp;

                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    /**
     * 向下调整
     * @param parent 父亲节点下标
     * @param len    向下调整的结束位置
     */
    private void siftDown(int parent, int len) {
        // 计算出孩子节点位置
        int child = parent * 2 + 1;
        // 开始向下调整
        while (child < len) {
            // 寻找出两个孩子节点中最大的
            if (child + 1 < len && ((T)queue[child]).compareTo(((T)queue[child + 1])) < 0) {
                child++;
            }

            // 与父亲节点进行判断，如果孩子节点比父亲节点大就进行调整 否则调整完毕
            if (((T)queue[child]).compareTo(((T)queue[parent])) < 0) {
                break;
            } else {
                T tmp = (T)queue[child];
                queue[child] = (T)queue[parent];
                queue[parent] = tmp;

                parent = child;
                child = parent * 2 + 1;
            }
        }
    }

    /**
     * 扩容方法
     */
    private void grow() {
        this.queue = Arrays.copyOf(this.queue, this.queue.length * 2);
    }

    private void display() {
        for (Object x : this.queue) {
            System.out.println(x);
        }
    }
}

三、使用优先级队列解决TopK问题

从上面优先级队列的介绍可知道，我们只需要创建出一个大小为K的优先级队列。当我们求前K的最小的元素时，我们只需要创建出一个大小为K的大根堆。首先让数组中k个元素进入堆中，然后从k+1开始遍历数组，在遍历过程中与堆顶的元素进行比较，这个时候堆顶的元素一定是这个堆中最大的一个，如果此时的值比堆顶的元素小就让这个元素替换堆顶的元素，依次往复，在遍历完整个数组后，这个堆中就会存储前K个最小元素。相反如果要寻找出最小的前K个数就创建大根堆重复操作

前K小的元素

public ArrayList<Integer> GetLeastNumbers_Solution (int[] input, int k) {
        // write code here
        ArrayList<Integer> ret = new ArrayList<>();
        if (k <= 0 || input == null) return ret;
        PriorityQueue<Integer> queue = new PriorityQueue<>(k, (o1, o2)->{return o2 - o1;});

        for (int i = 0; i < input.length; i++) {
            if (i < k) queue.offer(input[i]);
            else {
                if (input[i] < queue.peek()) {
                    queue.poll();
                    queue.offer(input[i]);
                }
            }
        }

        while (!queue.isEmpty()) {
            ret.add(queue.poll());
        }

        return ret;
    }
import java.util.*;




/**
 * @author 1886
 *
 */
  


public class Solution {
    static class PriorityQueue <T extends Comparable<T>> {
    // 优先级队列底层模拟堆的数组
    private Object[] queue;
    // 记录当前优先级队列元素个数
    private int size;

    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * 默认构造方法
     */
    public PriorityQueue() {
        this.queue = new Object[DEFAULT_INITIAL_CAPACITY];
    }

    /**
     * 指定大小
     * @param capacity
     */
    public PriorityQueue(int capacity) {
        this.queue = new Object[capacity];
    }

    /**
     * 传入指定数组
     * @param queue
     */
    public PriorityQueue(T[] queue) {
        // 1.初始化成员变量
        this.queue = queue;
        this.size = queue.length;

        // 2.将数组进行大根堆调整
        heapIfy();
    }

    /**
     * 入队操作
     * @param data 进入优先级队列的数据
     */
    public void offer(T data) {
        // 如果优先级队列满 进行扩容
        if (this.size == this.queue.length) {
            grow();
        }

        // 将元素放到末尾
        this.queue[this.size] = data;
        // 进行向上调整
        siftUp(this.size++);
    }

    /**
     * 出队操作
     * @return
     */
    public T poll() {
        // 如果为空就返回空
        if (this.size == 0) return null;

        // 将堆顶元素与最后一个位置进行交换
        T top = (T)queue[0];
        queue[0] = this.queue[this.size - 1];
        queue[this.size - 1] = top;

        // 删除元素
        this.size--;

        // 向下调整
        siftDown(0, this.size);

        // 返回
        return top;
    }

    /**
     * 排序
     */
    public void sort() {
        int len = this.size - 1;
        while (len >= 0) {
            T tt = (T) queue[0];
            queue[0] = queue[len];
            queue[len] = tt;

            siftDown(0, len--);
        }
    }

    /**
     * 堆化
     */
    private void heapIfy() {
        for (int parent = (this.size - 1 - 1) >> 1; parent >= 0; parent--) {
            siftDown(parent, this.size);
        }
    }

    /**
     * 向上调整
     * @param child
     */
    private void siftUp(int child) {
        // 计算出父亲节点的下标
        int parent = (child - 1) / 2;
        // 开始向上调整
        while (child > 0) {
            if (((T)queue[child]).compareTo((T)queue[parent]) >= 0) {
                T tmp = (T)queue[child];
                queue[child] = (T)queue[parent];
                queue[parent] = tmp;

                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    /**
     * 向下调整
     * @param parent 父亲节点下标
     * @param len    向下调整的结束位置
     */
    private void siftDown(int parent, int len) {
        // 计算出孩子节点位置
        int child = parent * 2 + 1;
        // 开始向下调整
        while (child < len) {
            // 寻找出两个孩子节点中最大的
            if (child + 1 < len && ((T)queue[child]).compareTo(((T)queue[child + 1])) < 0) {
                child++;
            }

            // 与父亲节点进行判断，如果孩子节点比父亲节点大就进行调整 否则调整完毕
            if (((T)queue[child]).compareTo(((T)queue[parent])) < 0) {
                break;
            } else {
                T tmp = (T)queue[child];
                queue[child] = (T)queue[parent];
                queue[parent] = tmp;

                parent = child;
                child = parent * 2 + 1;
            }
        }
    }

    public T peek() {
        return this.size == 0 ? null : (T)queue[0];
    }

    /**
     * 扩容方法
     */
    private void grow() {
        this.queue = Arrays.copyOf(this.queue, this.queue.length * 2);
    }

    private void display() {
        for (Object x : this.queue) {
            System.out.println(x);
        }
    }
}
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param input int整型一维数组 
     * @param k int整型 
     * @return int整型ArrayList
     */
    public ArrayList<Integer> GetLeastNumbers_Solution (int[] input, int k) {
        // write code here
        ArrayList<Integer> ans = new ArrayList<>();
        if (k <= 0 || input == null) return ans;

        PriorityQueue<Integer> queue = new PriorityQueue<>(k);
        for (int i = 0; i < input.length; i++) {
            if (i < k) queue.offer(input[i]);
            else if (input[i] < queue.peek()) {
                queue.poll();
                queue.offer(input[i]);
            }
        }

        while (queue.peek() != null) {
            ans.add(queue.poll());
        }
        return ans;
    }
}

四、快速选择算法解决TopK问题

快速选择

快速选择算法（Quickselect）是用于在未排序的数组中查找第k小或第k大元素的高效算法，它的时间复杂度为O(n)。该算法与快速排序有密切的联系，但它不对整个数组进行完整的排序，而是只关注于找到所需的特定顺序的元素。以下是它的一些关键点：

  1. 基本思想：
  • 选择一个基准值（pivot），按照这个基准值将数组分为两部分，左侧部分的所有元素都小于等于基准值，右侧部分的所有元素都大于基准值。
  1. 递归搜索：
  • 确定基准值的位置后，根据k与基准值的位置关系，选择数组的哪一部分继续进行递归搜索。如果k小于基准值的索引，则在第一部分（小于等于基准值的部分）继续搜索；否则，在第二部分（大于基准值的部分）继续搜索。
  1. 时间复杂度：
  • 快速选择算法的平均时间复杂度为O(n)，但最坏情况下的时间复杂度会退化到O(n^2)。尽管如此，由于其不需要完全排序数组，它在实际操作中通常比完全的排序算法更加高效。
  1. 实际应用：
  • 快速选择算法及其变种是在实际应用中最常使用的高效选择算法之一，尤其适用于解决Top K问题等场景。

总的来说，快速选择算法是一种基于快速排序的选择算法，它高效地解决了在不完全排序的数组中寻找特定顺序元素的问题，并因此在各种算法竞赛和实际应用场景中得到了广泛的使用。

图解快速选择

图解

对下面这个数组寻找到前k小的元素

首先我随机生成一个下标指向一个基准元素

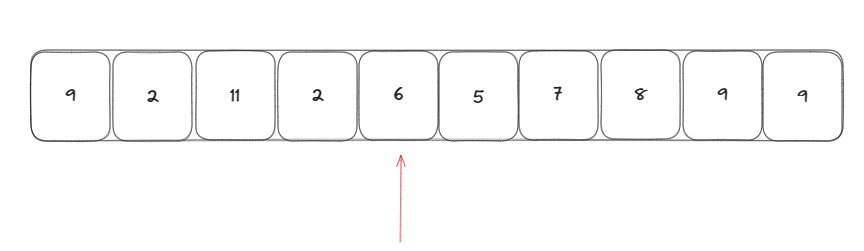
然后使用一个指针指向开始位置依次往后遍历，如果当前元素比基准元素大则将该元素放在末尾，也就是基准元素后面，如果比当前元素小则将他放在基准元素前面

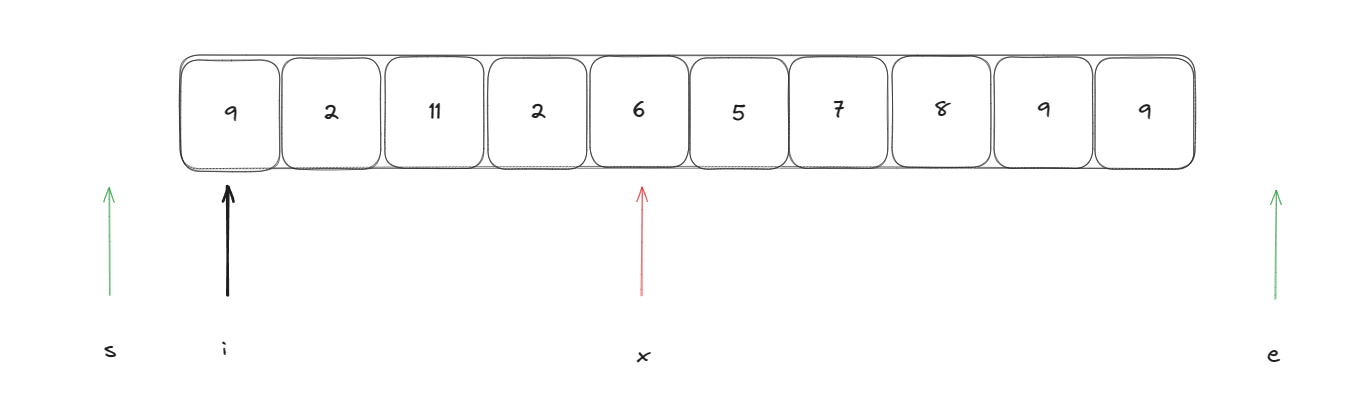
此时遍历指针i指向的值比基准元素大，此时需要执行以下操作进行交换：swap(arr[--e], arr[i])

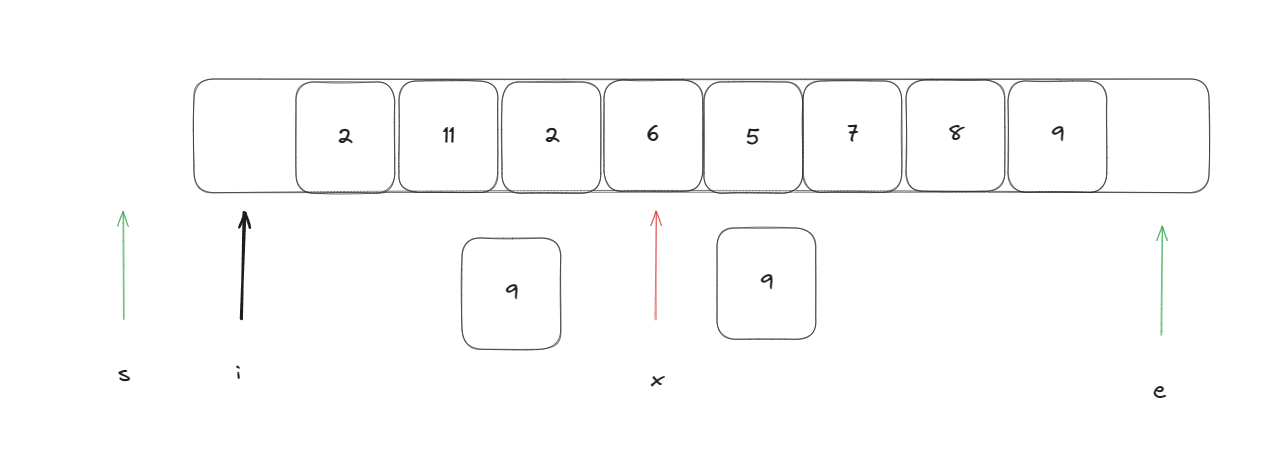
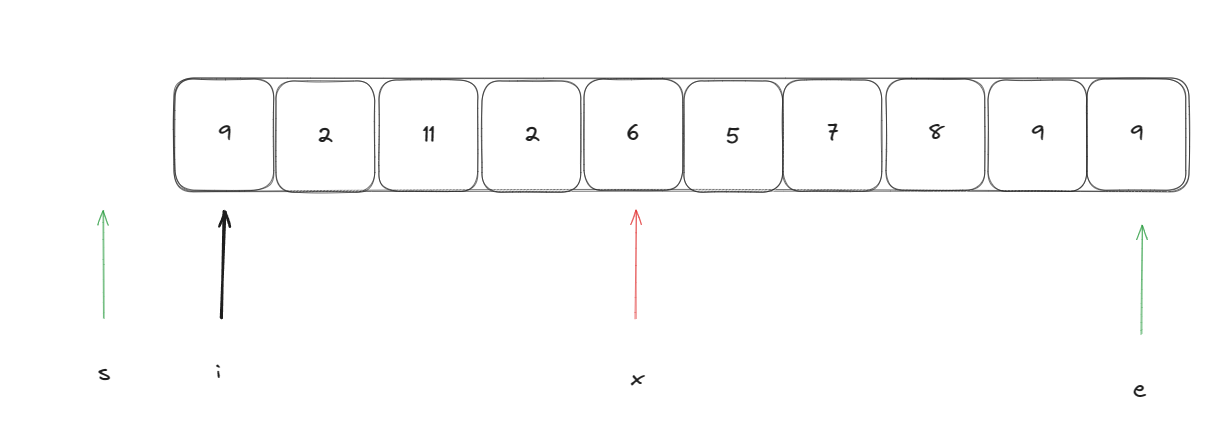
此时进行将遍历指针指向的元素与基准元素进行比较依次重复此操作，当遍历指针指向的元素比基准元素小时执行：swap(arr[i++], arr[++s]) ,当与基准元素相等时只需要执行i++即可。当遍历指针与末尾指针e相遇时即可停止。

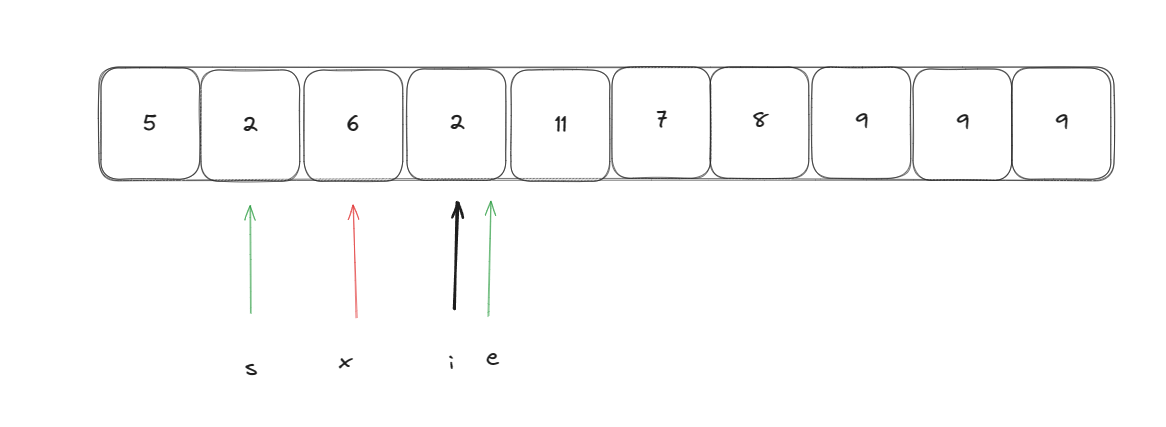
此时在l到s，e到r重复执行上述操作，知道l >= r时结束递归就是基于快速选择的快排算法。但是此时我们需要寻找前k小个元素，而数组已经被分成了三部分

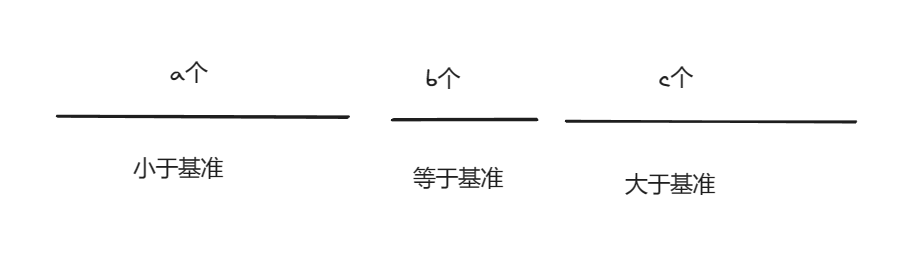
此时我们可以通过判断k是否小于等于a，如果k小于等于a那么前k小的元素一定是在左边这段区域，如果k小于等于a+b时说明此时第k小就在中间这个区域，只需要返回他就可以。如果上面两种情况都不成立，那么我们只需要区右边区域找到第k - a - b个最小的元素，找到该元素后，该元素之前的元素就是最小的K个数

代码解决前k小个元素

最小的K个数_牛客题霸_牛客网给定一个长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数。例如数组元素是。题目来自【牛客题霸】icon-default.png?t=N7T8https://www.nowcoder.com/practice/6a296eb82cf844ca8539b57c23e6e9bf?tpId=295&tqId=23263&ru=/exam/oj&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Foj

#include <vector>
class Solution {
public:
/**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param input int整型vector 
     * @param k int整型 
     * @return int整型vector
     */
int rand_num(int l, int r) {
    srand(time(0));
    return rand() % (r - l + 1) + l;
}

int qselect(vector<int>& arr, int l, int r, int k) {
    if (l >= r) return arr[l];
    int i = l, s = l - 1, e = r + 1, x = arr[rand_num(l,r)];
    while (i < e) {
        if (arr[i] > x) swap(arr[i], arr[--e]);
        else if (arr[i] < x) swap(arr[i++], arr[++s]);
        else i++;
    }
    int a = s - l + 1, b = e - s - 1;
    if (a >= k) return qselect(arr, l, s, k);
    else if (a + b >= k) return x;
    else return qselect(arr, e, r, k - a - b);
}

vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
    // write code here
    vector<int> ans(k);
    if (k <= 0 || input.size() < 1) return ans;
    qselect(input, 0, input.size() - 1, k);

    for (int i = 0; i < k; i++) ans[i] = input[i];
    return ans;
}
};

null有一个整数数组，请你根据快速排序的思路，找出数组中第 k 大的数。 给定一个整数数组。题目来自【牛客题霸】icon-default.png?t=N7T8https://www.nowcoder.com/practice/e016ad9b7f0b45048c58a9f27ba618bf?tpId=295&tqId=44581&ru=%2Fpractice%2F6a296eb82cf844ca8539b57c23e6e9bf&qru=%2Fta%2Fformat-top101%2Fquestion-ranking&sourceUrl=%2Fexam%2Foj

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param a int整型一维数组
     * @param n int整型
     * @param K int整型
     * @return int整型
     */
    private int randNum(int l, int r) {
        Random random = new Random();
        return l + random.nextInt(r - l + 1);
    }

    private void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    private int qSelect(int[] arr, int l, int r, int k) {
        if (l >= r) return arr[l];
        int i = l, s = l - 1, e = r + 1, x = arr[randNum(l, r)];
        while (i < e) {
            if (arr[i] > x) swap(arr, i, --e);
            else if (arr[i] < x) swap(arr, ++s, i++);
            else i++;
        }

        int c = r - e + 1, b = e - s - 1;
        if (c >= k) return qSelect(arr, e, r, k);
        else if (b + c >= k) return x;
        else return qSelect(arr, l, s, k - c - b); 
    }

    public int findKth (int[] a, int n, int K) {
        // write code here
        return qSelect(a, 0, n - 1, K);
    }
}

五、优先级队列与快速选则算法比较

优先级队列

使用优先级队列（通常实现为堆）解决TopK问题的时间复杂度是O(NlogK)。具体分析如下：

  1. 建堆：首先对K个元素进行建堆操作，建堆的时间复杂度是O(K)。这是因为堆的构建过程涉及到对K个元素进行排序，以形成一个最大堆或最小堆。
  2. 维护堆：然后遍历剩余的N-K个元素，对于每个元素，执行堆调整操作以维护堆的性质。每次插入或删除操作的时间复杂度是O(logK)，因为堆的高度大约是logK，而单次堆调整的时间复杂度与堆的高度成正比。因此，对于N-K个元素的遍历，总的时间复杂度是O((N-K)logK)。
  3. 总时间复杂度：综合以上两个步骤，总的时间复杂度是O(K + (N-K)logK)，由于通常情况下K远小于N，可以简化为O(NlogK)。
快速选择

快速选择算法的平均时间复杂度是 O(N)，但最坏情况下的时间复杂度是 O(N^2)。以下是关于快速选择算法时间复杂度的详细分析：

  1. 平均时间复杂度：
  • 在平均情况下，快速选择算法的时间复杂度是O(N)。这是因为每次分区操作平均只需要遍历数组的一半长度。在快速选择算法中，我们选择一个枢纽元素（pivot），并将数组分为两部分，一部分包含小于枢纽的元素，另一部分包含大于枢纽的元素。这个过程与快速排序相似，但是快速选择只递归地处理包含第K小元素的那一部分数组，而不是整个数组。由于每次递归调用处理的数组大小大约减半，所以平均时间复杂度为O(N)。
  1. 最坏情况时间复杂度：
  • 在最坏的情况下，如果每次选择的枢纽都是最大或最小元素，那么每次分区操作只能减少一个元素的大小，导致需要进行N次分区操作，因此最坏情况下的时间复杂度是O(N^2)。为了减少这种情况的发生，可以通过随机选择枢纽来提高算法的效率。
  1. 优化措施：
  • 为了优化快速选择算法并避免最坏情况的发生，可以采用“中位数的中位数”作为枢纽，这种方法被称为BFPRT算法。通过计算近似中位数并将其作为枢纽，可以有效地将数组分为大致相等的两部分，从而保持算法的平均时间复杂度。
  1. 数学推导：
  • 快速选择算法的时间复杂度也可以通过数学归纳法进行推导。可以将数组分成若干组，每组选取中位数，然后从中选取中位数的中位数作为枢纽。这样的分组策略可以保证至少有一部分数组的大小显著减少，从而在数学上证明算法的平均时间复杂度为O(N)。具体的推导过程涉及到递归式和分组策略的详细分析。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1482203.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mybatis plus核心功能-IService

Mybatis plus核心功能-IService

目录 1 前言 2 使用方法 2.1 继承ServiceImpl,> 2.2 基础业务开发的使用 2.3 复杂业务开发的使用 2.3 Lambda查询 2.4 Lambda更新 1 前言 我本以为Mapper层的类能够继承BaseMapper<XXX>&#xff0c;而不用我们手动写一些mapper方法已经够离谱了。没想到海油膏…
阅读更多...
Zookeeper学习1：概述、安装、应用场景、集群配置

Zookeeper学习1：概述、安装、应用场景、集群配置

文章目录 概述安装LinuxWindows 配置参数集群参考配置文件配置步骤流程启动 概述 Zookeeper&#xff1a; 为分布式框架组件提供协调服务的中间件 【类似&#xff1a;文件系统通知机制】 负责存储上下层应用关系的数据以及接收观察者注册监听&#xff0c;一旦观察查关心的数据发…
阅读更多...
gpt批量工具,gpt批量生成文章工具

gpt批量工具,gpt批量生成文章工具

GPT批量工具在今天的数字化时代扮演着越来越重要的角色&#xff0c;它们通过人工智能技术&#xff0c;可以自动批量生成各种类型的文章&#xff0c;为用户提供了便利和效率。本文将介绍5款不同的GPT批量工具&#xff0c;并介绍一款知名的147GPT生成工具&#xff0c;以及另外一款…
阅读更多...
MyBatis的补充用法

MyBatis的补充用法

说明&#xff1a;之前介绍过MyBatis的用法&#xff0c;像 用注解和Mapper.xml操作数据库、在Mapper.xml里写动态SQL。最近在一次用MyBatis批量更新数据库对象的场景中&#xff0c;意识到对MyBatis的一些标签用法不太熟悉&#xff0c;所以去 MyBatis官网 看了一些文档&#xff0…
阅读更多...
（介绍与使用）物联网NodeMCUESP8266（ESP-12F）连接新版onenet mqtt协议实现上传数据（温湿度）和下发指令（控制LED灯）

（介绍与使用）物联网NodeMCUESP8266（ESP-12F）连接新版onenet mqtt协议实现上传数据（温湿度）和下发指令（控制LED灯）

前言 本文详细介绍了如何利用物联网技术，通过NodeMCU ESP8266（ESP-12F）模块连接到新版的OneNet平台，使用MQTT协议实现数据的上传与指令的下发。文中首先对NodeMCU ESP8266模块及其特性进行了简介，随后详细阐述了如何配置和使用MQTT协议连接到OneNet平台，实现温湿度数据的…
阅读更多...
亚信安慧AntDB：融合架构下的数据管理利器

亚信安慧AntDB：融合架构下的数据管理利器

AntDB的独特架构将集中式和分布式部署模式巧妙融合&#xff0c;为用户提供了全方位的数据管理解决方案。这种一站式的特性使得用户无需在不同系统间来回切换&#xff0c;极大地提高了工作效率。 AntDB同时具备集中式和分布式系统的优点&#xff0c;集中式架构拥有简单易用、管…
阅读更多...
Java对象大小计算

Java对象大小计算

概述 在实际应用中&#xff0c;尤其是在进行JVM调优时&#xff0c;理解并正确估计对象大小是非常重要的&#xff0c;因为这直接影响到内存分配、垃圾回收效率以及应用程序的整体性能。 对象的组成 在Java中&#xff0c;计算一个对象的大小是为了了解它在内存中占用的确切空间…
阅读更多...
Leetcode2673. 使二叉树所有路径值相等的最小代价

Leetcode2673. 使二叉树所有路径值相等的最小代价

Every day a Leetcode 题目来源&#xff1a;2673. 使二叉树所有路径值相等的最小代价 解法1&#xff1a;遍历 对于满二叉树&#xff0c;父节点 cost[i] 的左右儿子节点分别为 cost[2 * i - 1]、cost[2 * i]。 考虑根到两个互为兄弟节点&#xff08;父节点相同&#xff09;的…
阅读更多...
什么是VR虚拟社区|VR元宇宙平台|VR主题馆加盟

什么是VR虚拟社区|VR元宇宙平台|VR主题馆加盟

VR虚拟社区是指一种基于虚拟现实技术构建的在线社交平台或环境&#xff0c;用户可以在其中创建虚拟化的个人形象&#xff08;也称为avatars&#xff09;并与其他用户进行交流、互动和合作。在VR虚拟社区中&#xff0c;用户可以选择不同的虚拟场景和环境&#xff0c;如虚拟公园、…
阅读更多...
Navicat保存的连接密码破解-java代码

Navicat保存的连接密码破解-java代码

第一步&#xff1a;找到加过密的密码 有两种方法可以找到密码&#xff0c;一种是注册表里可以找到&#xff0c;一种是导出连接信息功能&#xff0c;这里说第二种。 1、打开Navicat&#xff0c;点击文件->导出连接菜单 2、导出要破解密码的连接到connections.ncx文件中&…
阅读更多...
小程序配置服务器域名的操作步骤（入门级）

小程序配置服务器域名的操作步骤（入门级）

将详细列出小程序配置服务器域名的操作步骤&#xff1a; 服务器选购推荐&#xff1a;腾讯云轻量服务器 点击以下任一云产品链接&#xff0c;跳转后登录&#xff0c;自动享有所有云产品优惠权益&#xff1a; 经过笔者亲测&#xff0c;强烈推荐腾讯云轻量应用服务器作为游戏服…
阅读更多...
SQL面试题（2）

SQL面试题（2）

第一题 创建trade_orders表： create table `trade_orders`( `trade_id` varchar(255) NULL DEFAULT NULL, `uers_id` varchar(255), `trade_fee` int(20), `product_id` varchar(255), `time` varchar(255) )ENGINE = InnoDB CHARACTER SET = utf8mb4 COLLATE = utf8mb4_0900_…
阅读更多...
11-orm-自研微服务框架

11-orm-自研微服务框架

ORM 当开发涉及到存储数据的时候&#xff0c;往往要用到数据库&#xff0c;用的最多的就是mysql了&#xff0c;这里我们实现一个orm&#xff0c;让开发者更加便捷的操作数据库 1. Insert实现 orm的本质就是拼接sql&#xff0c;让开发者更加方便的使用 package ormimport ("…
阅读更多...
物联网技术助力智慧城市安全建设：构建全方位、智能化的安全防护体系

物联网技术助力智慧城市安全建设：构建全方位、智能化的安全防护体系

一、引言 随着城市化进程的加速和信息技术的迅猛发展&#xff0c;智慧城市已成为现代城市发展的重要方向。在智慧城市建设中&#xff0c;安全是不可或缺的一环。物联网技术的快速发展为智慧城市安全建设提供了有力支持&#xff0c;通过构建全方位、智能化的安全防护体系&#…
阅读更多...
百度百科人物创建要求是什么？

百度百科人物创建要求是什么？

百度百科作为我国最大的中文百科全书&#xff0c;其收录的人物词条要求严谨、客观、有权威性。那么&#xff0c;如何撰写一篇高质量的人物词条呢&#xff1f;本文伯乐网络传媒将从内容要求、注意事项以及创建流程与步骤三个方面进行详细介绍。 一、内容要求 1. 基本信息&#…
阅读更多...
spring-boot-starter-parent和spring-boot-dependencies介绍

spring-boot-starter-parent和spring-boot-dependencies介绍

springboot项目的pom文件中&#xff0c;我们经常看见这样(下图)两种springboot的版本依赖管理方式&#xff1b;图片中的这两种依赖声明方式任意用其中一种都可以。文章后面会简单阐述一下区别和使用场景。 事例中完整的pom文件 <?xml version"1.0" encoding&quo…
阅读更多...
UnityShader——09数学知识3

UnityShader——09数学知识3

方阵 行与列数量相等的矩阵,n*n阶矩阵 对角矩阵 当对角线以外的矩阵内元素全为0&#xff0c;则称之为对角矩阵&#xff0c;对角矩阵的前提是必须是方阵 单位矩阵 对角线元素全为1&#xff0c;其余元素全为0&#xff0c;属于对角矩阵的一部分 矩阵和向量 把1 * n阶矩阵称…
阅读更多...
C++设计模式_创建型模式_工厂方法模式

C++设计模式_创建型模式_工厂方法模式

目录 C设计模式_创建型模式_工厂方法模式 一、简单工厂模式 1.1 简单工厂模式引入 1.2 简单工厂模式 1.3 简单工厂模式利弊分析 1.4 简单工厂模式的UML图 二、工厂方法模式 2.1 工厂模式和简单工厂模式比较 2.2 工厂模式代码实现 2.3 工厂模式UML 三、抽象工厂模式 3.1 战斗场景…
阅读更多...
实现定时器的两种方法：使用windows api定时器 和使用c++11/14 定时器

实现定时器的两种方法：使用windows api定时器 和使用c++11/14 定时器

前言&#xff1a; 当我有一个开发需求&#xff0c;符合下面的条件 1.需要某个任务在程序中每隔一段时间就要执行一次&#xff0c;可能把这个任务封装成了一个函数。 2.这种需要定时执行的任务&#xff0c;有2个&#xff0c;3个....越来越多。 这个时候我们就可以考虑使用定时…
阅读更多...
laravel ApiResponse接口统一响应封装

laravel ApiResponse接口统一响应封装

一&#xff0c;新增接口返回码配置文件 在config中新增配置文件apicode.php <?phpreturn [ apicodes>[/*** Message("OK")* 对成功的 GET、PUT、PATCH 或 DELETE 操作进行响应。也可以被用在不创建新资源的 POST 操作上*/HTTP_OK > 200,/*** Message(&qu…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023