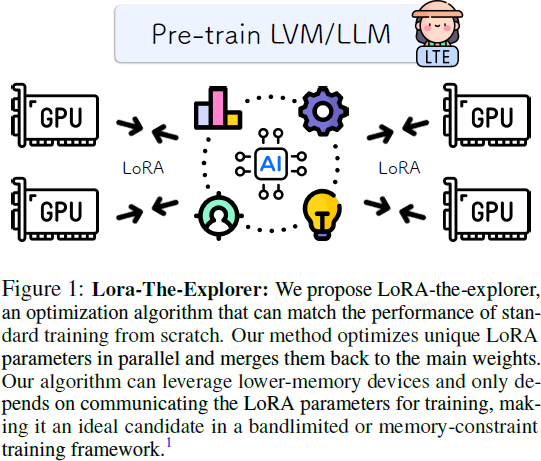
Training Neural Networks from Scratch with Parallel Low-Rank Adapters

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

2. 基础

3. 方法

3.1. 动机：多头合并的视角

3.2. LoRA soup：延迟 LoRA 合并

3.3. LoRA-the-Explorer：并行低秩更新

4. 实验

---

0. 摘要

深度学习模型的可扩展性在根本上受到计算资源、内存和通信的限制。尽管像低秩适应（LoRA）这样的方法降低了模型微调的成本，但其在模型预训练中的应用仍然相对未被深入探讨。本文探讨了将 LoRA 扩展到模型预训练，识别了在这一背景下标准 LoRA 的固有约束和局限性。我们引入了 LoRA-the-Explorer（LTE），这是一种新颖的双层优化算法，旨在实现在计算节点上并行训练多个低秩头，从而减少频繁同步的需求。我们的方法在使用各种视觉数据集的视觉 transformer 上进行了大量实验，表明 LTE 在标准预训练中具有竞争力。

项目页面：minyoungg.github.io/LTE

2. 基础

3. 方法

为了理解使用 LoRA 进行预训练所需的条件，我们首先确定了一种具体的情景，在这种情景下，可以使用 LoRA 恢复标准训练性能。这为我们开发算法提供了指导，该算法保持了 LoRA 的内存效率。

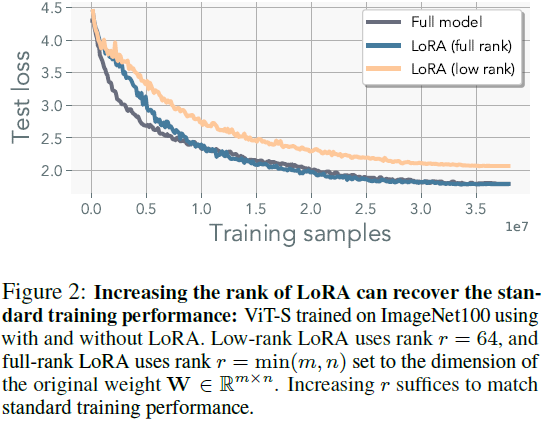
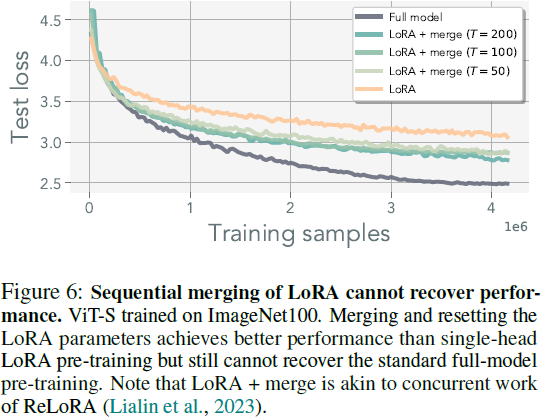
尽管低秩适应器（LoRA）已被证明是一种有效的微调方法，但在预训练时它们存在明显的限制。正如图 2 所示，使用 LoRA 参数化的模型表现出比使用标准优化训练的模型更差的性能。这种性能差距并不令人惊讶，因为它可以归因于 LoRA 中固有的秩约束。具体而言，对于参数 W∈ R^(m×n)，LoRA 基本上无法恢复超过秩 r < min(m, n) 的权重。当然，也有一些例外情况，偶然情况下，一个解存在于初始化的低秩邻域内。然而，在附录 B 中，我们观察到梯度的秩在训练过程中往往会增加，暗示了高秩更新的必要性。

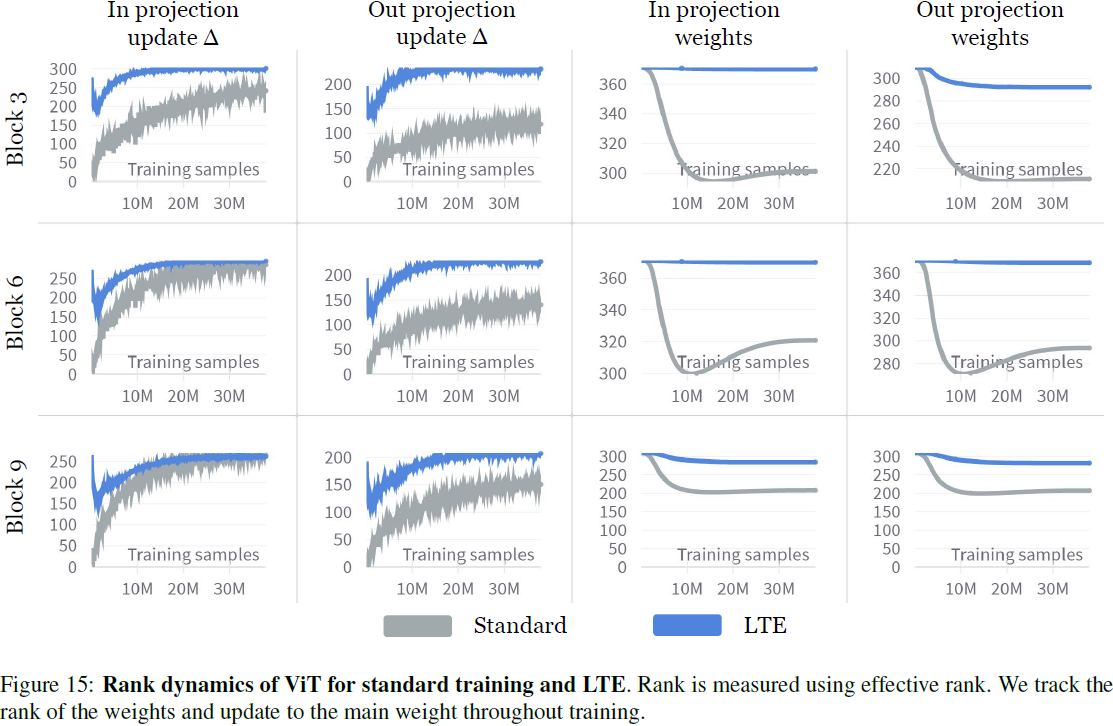
3.1. 动机：多头合并的视角

本节提供关于为什么 LoRA 并行使用多个头可以达到标准预训练性能的直观解释。

正如图 2 所示，将 LoRA 的秩 r 提高到与权重矩阵 W ∈ R^(m×n) 的秩 min(m, n) 相同足以复制标准预训练性能，尽管在附录 B.2 中详细说明了其中不同的内在动态。然而，这种方法会损害低秩适应器的内存效率。

因此，我们调查通过并行使用多个低秩适应器来达到等效性能的可能性。我们的动机利用了这些适应器的线性特性来引入并行化的简单想法。

给定形式为 BA ∈ R^(d1×d2） 的矩阵，其中 B ∈ R^(d1×d) 和 A ∈ R^(d×d2)，可以将乘积表示为两个低秩矩阵的和：B1A1+B2A2。为了证明这一点，让 bi 和 ai 分别是 B 和 A 的列向量。然后可以构造 B1 = [b_1, . . . , b_[d/2]]，B2 = [b_[d/2], . . . , b_d]，以及 A1 = [a_1，. . . ，a_[d/2]]^T，A2 = [a_[d/2]，. . . ，a_d]^T。这种分解允许通过较低秩矩阵的线性组合来逼近高秩矩阵。通过从秩-1 矩阵的线性组合开始，可以得出相同的结论。这构成了一种新颖的多头 LoRA 参数化方法，我们将其用作与我们最终方法进行比较的基线之一。

Multi-head LoRA（MHLoRA）：给定矩阵 W ∈ R^(m×n) 和常数 N，多头 LoRA 将权重参数化为N 个低秩矩阵 Bn 和 An 的线性组合：

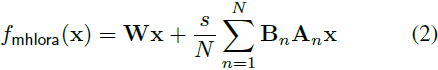
多头 LoRA 将全秩权重重新参数化为低秩权重的线性组合。

现在，我们将指出一个微不足道的观察结果，即单个并行 LoRA 头可以近似多头 LoRA 的单个步骤的轨迹，前提是定期将并行 LoRA 头合并到完整权重中。

对所有 LoRA 参数使用相同的秩 r，单个并行 LoRA 头（用 ˆ· 表示）的动态与多头 LoRA 等效： 

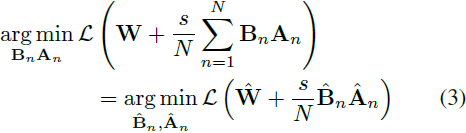
当

等于 ^Bn​^An​，或

时，等式 3 成立；这里我们使用了一种简写符号，表示求和是对所有 LoRA 参数（除了索引n）进行的。我们假设方程两边的参数被初始化为相同的值：对于所有 n，^An​ = An​ 且 Bn ​= ^Bn​。

第一种情况是秩亏的，我们知道它无法恢复原始的模型性能。后一种情况要求 ^W 在每次迭代中累积所有 LoRA 参数的信息。因此，如果我们可以在每次迭代中应用合并运算符，我们就可以恢复精确的更新。

这个相当简单的观察意味着我们可以恢复多头 LoRA 参数化模型的精确梯度更新，我们观察到这些更新在各种任务中与预训练性能相匹配（请参见附录 D）。此外，在分布式设置中，只需在设备之间传递 LoRA 参数/梯度，这通常是原始模型大小的一小部分，这使其成为在计算节点之间的互连速度有限的情况下的良好选择。

3.2. LoRA soup：延迟 LoRA 合并

为了进一步降低 LTE 的通信成本，我们延伸并结合了局部更新（McMahan等，2017）和模型平均（Wortsman等，2022；Yadav等，2023；Ilharco等，2023）的思想。我们允许 LoRA 参数在合并运算符之前独立训练更长的时间，而不是每次迭代都进行合并。这相当于使用 LoRA 参数的过时估计（stale estimates）

其中 ′ 表示参数的过时估计。

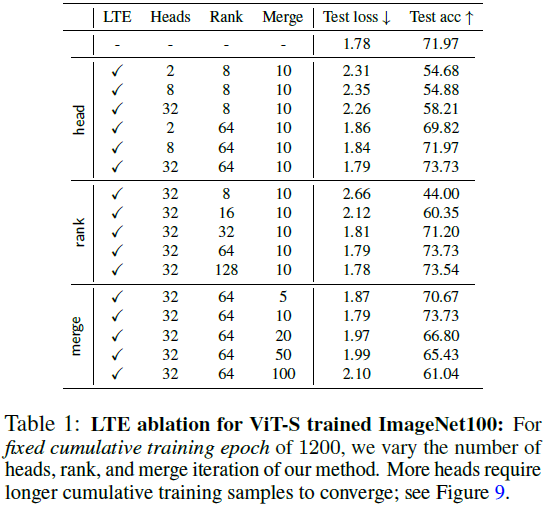
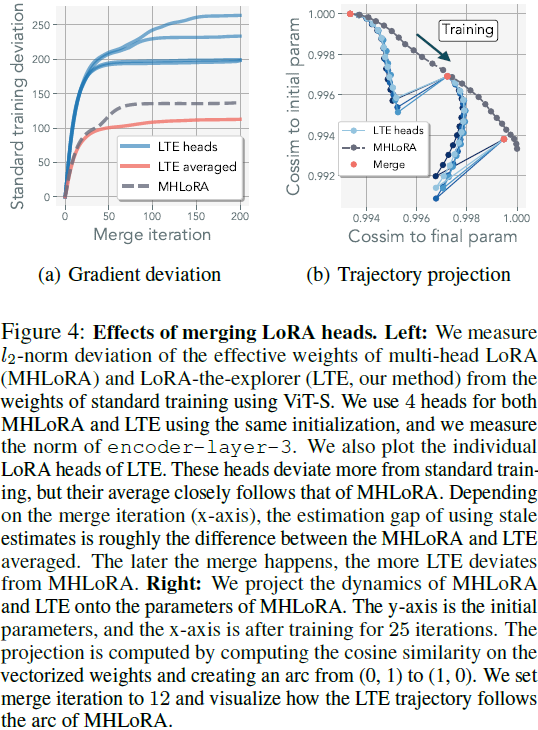
每次迭代合并确保表示不会偏离预期的更新。虽然使用过时的估计会放宽这种等价性，但我们观察到它仍然可以匹配表 1 中所示的标准训练性能。然而，随着估计变得不准确，优化轨迹确实会偏离多头 LoRA 的优化路径。我们在图 4 中量化了这种偏差。这种偏离并不意味着模型不能优化；相反，它表明优化轨迹将偏离多头 LoRA 的轨迹。在这项工作中，我们选择了简单的平均方法，将更复杂的合并方法留给未来的工作，例如 (Karimireddy等，2020；Matena＆Raffel，2022；Yadav等，2023)。

3.3. LoRA-the-Explorer：并行低秩更新

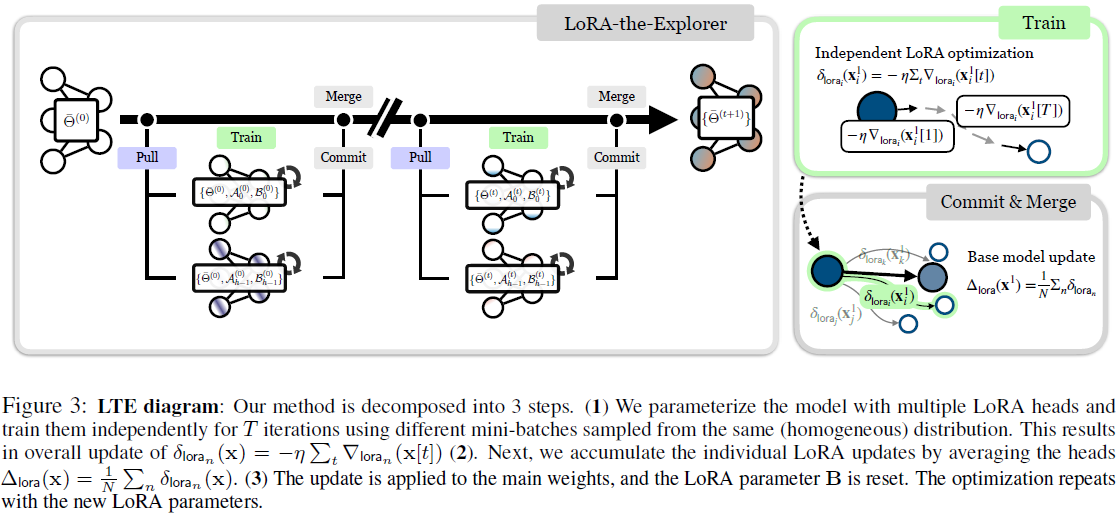
我们的算法设计考虑了两个主要因素：（1）实现一个具有信息量的更新 ΔW，在训练过程中不需要完整参数大小的实现，以及（2）对 W 进行参数化，使其可以以低精度存储和高效传递。后者可以通过使用量化权重并保留 W 的高精度副本来实现。 我们提出了 LoRA-the-Explorer（LTE），这是一种通过并行低秩更新来近似全秩更新的优化算法。该算法在初始化时为每个线性层创建 N 个不同的 LoRA 参数。每个工作器被分配 LoRA 参数，并创建一个局部优化器。接下来，数据从相同的分布中独立采样 x={x1​,...xN​}。对于每个 LoRA 头 n，参数根据其自己的数据分区进行 T 次迭代优化，导致更新

我们不同步工作器之间的优化器状态。优化之后，同步生成的 LoRA 参数以计算主要权重

的最终更新。 在下一个训练周期中，LoRA 参数将使用更新后的权重 W 进行训练。在这里，LoRA参数可以重新初始化，也可以使用相同的参数与修正项（参见附录A.2）。由于我们不直接在主参数 W 上进行训练，我们可以使用量化参数 q(W)。其中，可以将高精度权重保留在主节点上，也可以在训练期间从设备卸载它。这不仅减少了每个工作器的内存占用，还减少了传输开销。算法 1 中提供了伪代码，图 3 中提供了插图。

4. 实验