力扣2月最后三天的每日一题
- 前言
- 2867.统计树中的合法路径数目
- 思路
- 确定1e5中的质数
- 统计每个点的连接情况
- 开始对质数点进行处理
- 完整代码
- 2673.使二叉树所有路径值相等的最小代价
- 思路
- 完整代码
- 2581.统计可能的树根数目
- 思路
- 建立连通关系
- 将猜测数组变为哈希表,方便查询
- 利用dfs初始化根为0的猜测正确数量
- 统计完整的结果
前言
不会做,全靠灵神的视频讲解
2867.统计树中的合法路径数目
思路
考虑质数节点,每个质数节点应该都有属于它自己的多个连通块,而每个连通块中存在的非质数路径那么就可以形成一条合法路径
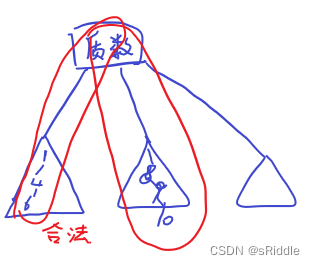
所以我们需要去统计一个质数的连通块中有多少非质数的连通情况,最后结果相加即可
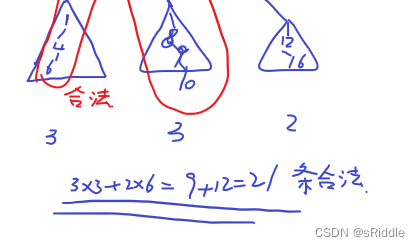
确定1e5中的质数
对于一个质数,其的倍数一定不是质数
void checknp(bool* np)
{
np[1] = true;
for(int i = 2;i*i<MX+1;i++)
{
for(j = i*i ;j <MX+1;j+=i)
{
if(!np[i])
{
np[j] = true;
}
}
}
}
统计每个点的连接情况
根据传入参数edgs数组,可以得到每个点与哪些点连接
vector<vector<int>> connect(n+1);
for(auto edge : edges)
{
connect[edge[0]].push_back(edge[1]);
connect[edge[1]].push_back(edge[0]);
}
开始对质数点进行处理
我们需要用到记忆化搜索的技巧。当我们对一个非质数与哪些非质数连接情况进行讨论后,我们可以将结果存储,如果后面有质数节点也与该非质数节点连接,那么就可以直接使用了。
//记录返回值 和 记忆化存储非质数节点与多少个非质数节点连接
long long res = 0;
vector<int> mem(n+1);
for(int i = 1;i<n+1;i++)
{
//如果是非质数,就可以跳过,因为我们只考虑质数的连通
if(np[i]) continue;
//记录连通数
int sum = 0;
//对i的连通点进行处理结果
for(int j : connect[i])
{
//只考虑非质数的情况
if(!np[j]) continue;
//如果没有被搜索过
if(mem[j] == 0)
{
//存储相互连接节点的数组清空
nodes.clear();
checknodes(j,-1,connect);
//对于nodes数组里面的所有点,其连通点的个数都是nodes数组的长度
for(int k : nodes)
{
mem[k] = nodes.size();
}
}
//计算结果,质数i下面的j连通块
res += mem[j] * sum;
sum += mem[j];
}
//以质数为头的结果
res += sum;
}
完整代码
const int MX = 1e5;
class Solution {
private:
bool np[MX+1];
vector<int> nodes;
public:
void checknp(bool* np)
{
np[1] = true;
for(int i = 2;i*i<MX+1;i++)
{
for(int j = i*i ;j <MX+1;j+=i)
{
if(!np[i])
{
np[j] = true;
}
}
}
}
void checknodes(int x,int fa,vector<vector<int>>& connect)
{
nodes.push_back(x);
for(int y:connect[x])
{
if(y!=fa&&np[y])
{
checknodes(y,x,connect);
}
}
}
public:
long long countPaths(int n, vector<vector<int>>& edges) {
checknp(np);
vector<vector<int>> connect(n+1);
for(auto edge : edges)
{
connect[edge[0]].push_back(edge[1]);
connect[edge[1]].push_back(edge[0]);
}
//结果
long long res = 0;
//记忆化搜索
vector<int> mem(n+1);
for(int i = 1;i<n+1;i++)
{
if(np[i]) continue;
//记录当前节点的连接数
int sum = 0;
for(int j : connect[i])
{
if(!np[j]) continue;
//如果没被遍历过
if(mem[j] == 0)
{
nodes.clear();
checknodes(j,-1,connect);
//修改记忆存储结果
for(int k : nodes)
{
mem[k] = nodes.size();
}
}
//统计该连通块对结果的影响
res += mem[j]*sum;
sum += mem[j];
}
//已质数节点为头的情况
res += sum;
}
return res;
}
};
2673.使二叉树所有路径值相等的最小代价
思路
从叶子节点开始,计算根节点到该叶子节点的路径和,然后修改其中一个叶子节点使得和相等,由于只能增加,所以向大值修改。
修改完成后将该和返回给叶子节点的父节点,然后比较同一层级的父节点的和,进行修改。
逐步返回直到根节点
完整代码
对于满二叉树,父节点和左右子结点在数组中存在一个关系。
class Solution {
public:
int minIncrements(int n, vector<int>& cost) {
//统计每个节点的路径和
for(int i = 2;i<n+1;i++)
{
cost[i-1] += cost[i/2-1];
}
//更新结果
int res = 0;
for(int i = n/2;i>0;i--)
{
res += abs(cost[2*i]-cost[2*i-1]);
cost[i-1] = max(cost[2*i],cost[2*i-1]);
}
return res;
}
};
2581.统计可能的树根数目
思路
还不是很明白
我们假设以0为根的正确猜测是cnt0,那调换到以1为根,那么cnt1的值
首先需要减去guesses数组[0,1]的数量,再加上[1,0]的数量,因为[u,v]表示u是v的父节点。
其余调换类似。
建立连通关系
vector<vector<int>> g(edges.size() + 1);
for (auto &e : edges)
{
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}
将猜测数组变为哈希表,方便查询
unordered_set<LL> s;
for (auto &e : guesses)
{ // guesses 转成哈希表
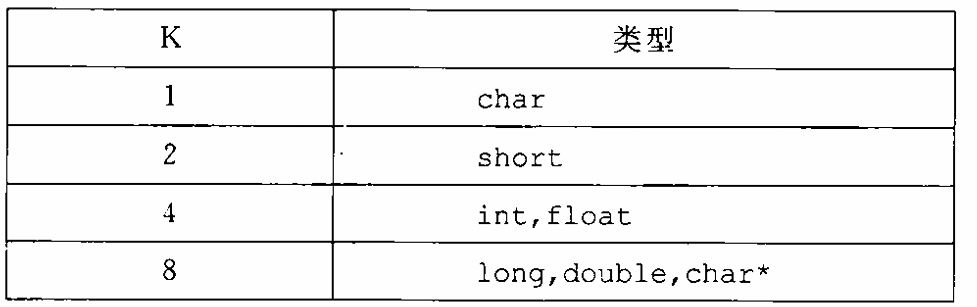
s.insert((LL) e[0] << 32 | e[1]); // 两个 4 字节数压缩成一个 8 字节数
}
利用dfs初始化根为0的猜测正确数量
int ans = 0, cnt0 = 0;
function<void(int, int)> dfs = [&](int x, int fa)
{
//y与x连通
for (int y : g[x])
{
//y不是父节点,防止反向计算
if (y != fa)
{
//[x,y]如果存在哈希表中,表面以0为根的结果猜测正确+1
cnt0 += s.count((LL) x << 32 | y); // 以 0 为根时,猜对了
//以当前节点为父节点搜索子结点
dfs(y, x);
}
}
};
dfs(0, -1);
统计完整的结果
//计算以x为根的cnt
function<void(int, int, int)> reroot = [&](int x, int fa, int cnt)
{
ans += cnt >= k; // 此时 cnt 就是以 x 为根时的猜对次数
for (int y : g[x])
{
if (y != fa)
{
//从0开始,变换根为0的连通节点,在变换为连通节点的连通节点
reroot(y, x, cnt
- s.count((LL) x << 32 | y) // 原来是对的,现在错了
+ s.count((LL) y << 32 | x)); // 原来是错的,现在对了
}
}
};
reroot(0, -1, cnt0);