给你一棵二叉树的根节点 root ，找出并返回满足要求的节点数，要求节点的值等于其 子树 中值的 平均值 。

注意：

n 个元素的平均值可以由 n 个元素 求和 然后再除以 n ，并 向下舍入 到最近的整数。
root 的 子树 由 root 和它的所有后代组成。

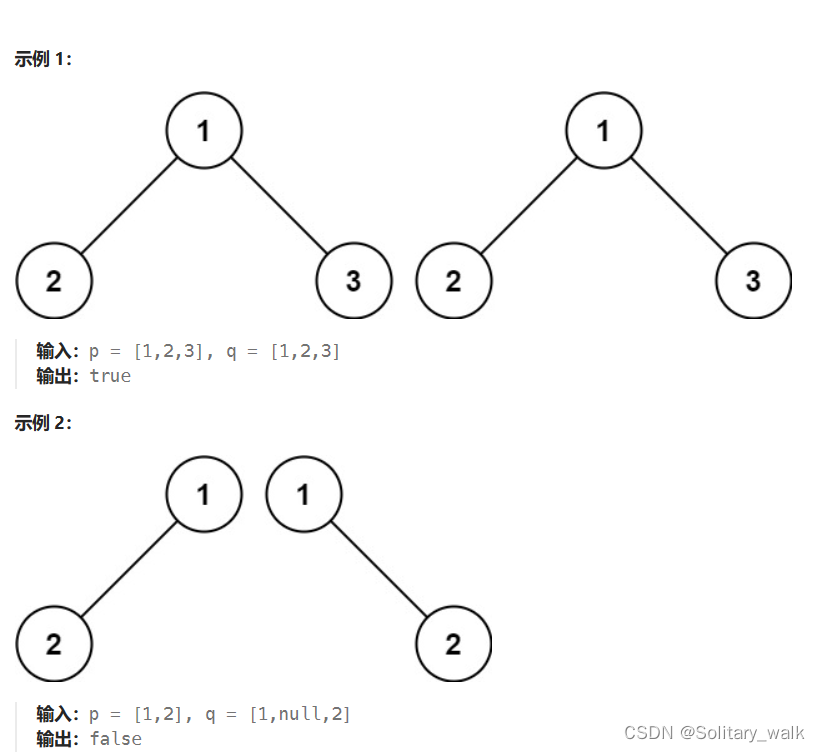
示例 1：

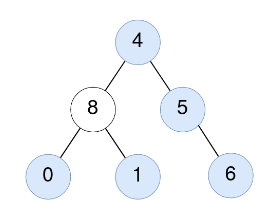
输入：root = [4,8,5,0,1,null,6]
输出：5
解释：
对值为 4 的节点：子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
对值为 5 的节点：子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
对值为 0 的节点：子树的平均值 0 / 1 = 0 。
对值为 1 的节点：子树的平均值 1 / 1 = 1 。
对值为 6 的节点：子树的平均值 6 / 1 = 6 。
示例 2：

输入：root = [1]
输出：1
解释：对值为 1 的节点：子树的平均值 1 / 1 = 1。

提示：

树中节点数目在范围 [1, 1000] 内
0 <= Node.val <= 1000

递归dfs后序遍历模拟：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int averageOfSubtree(TreeNode* root) {
        int ans = 0;
        getNumAndSum(root, ans);

        return ans;
    }

private:
    vector<int> getNumAndSum(TreeNode *node, int &ans)
    {
        if (node == nullptr)
        {
            return {0, 0};
        }

        vector<int> left = getNumAndSum(node->left, ans);
        vector<int> right = getNumAndSum(node->right, ans);

        ans += static_cast<int>((left[1] + right[1] + node->val) / (left[0] + right[0] + 1)) == node->val;

        return {left[0] + right[0] + 1, left[1] + right[1] + node->val};
    }
};

如果树中有n个节点，则此算法时间复杂度为O(n)，空间复杂度为O(lgn)。