目录
2.7 范式
2.7.1 范式的定义
2.7.2 范式存在定理
2.8 主析取范式和主合取范式
2.8.1 极小项和极大项的定义和编码
2.8.2 极小项和极大项的性质
2.8.3 主析取范式和主合取范式的定义
2.8.4 主范式求解定理
2.8.5 真值表技术
2.8.6 范式的相互转化
2.8.7 主范式的应用
2.9 基本推理形式和蕴涵公式
2.9.1 推理的基本形式
2.9.2 推理的判定定理及判定方法
2.9.3 推理定律–基本蕴涵关系
2.10 自然演绎法推理
2.10.1 推理规则
2.10.2 自然演绎法
2.10.3 直接证明法
2.10.4 规则 CP 证明法
2.10.5 间接证明法(反证法,归谬法)
2.10.6 推理的应用
2.7 范式
2.7.1 范式的定义
命题变元或命题变元的否定称为文字。P, ¬P, Q, ¬Q, · · ·
有限个(包括单个)文字的析取称为简单析取式(或子句)。P ∨ Q ∨ ¬R, · · · P,¬P
有限个(包括单个)文字的合取称为简单合取式(或短语)。¬P ∧ Q ∧ R, · · · P,¬P
P 与 ¬P 称为互补对
有限个(包括单个)简单合取式(短语)的析取式称为析取范式(disjunctive normal form)
如 (P ∧ Q) ∨ (¬P ∧ Q) ,又如 P ∧ ¬Q,P,¬P
有限个(包括单个)简单析取式(子句)的合取式称为合取范式(conjunctive normal form)
如 (P ∨ Q) ∧ (¬P ∨ Q) ,又如 P ∨ ¬Q,P, ¬P
- P, ¬P 是文字,短语,子句,析取范式,合取范式
- P ∨ Q ∨ ¬R 是子句,合取范式,析取范式;(P ∨ Q ∨ ¬R) 是子句,合取范式。
- ¬P ∧ Q ∧ R 是短语,析取范式,合取范式;(¬P ∧ Q ∧ R) 是短语,析取范式。
- P ∨ (Q ∨ ¬R) 即不是析取范式也不是合取范式,但转换为 P ∨ Q ∨ ¬R 后,即是析取范式和合取范式。
小结
- 范式关注的是命题公式的当前书写形式;
- 单个的文字是子句、短语、析取范式,合取范式;
- 析取范式、合取范式仅含联结词集 {¬, ∧, ∨},且否定联接词仅出现在命题变元之前
2.7.2 范式存在定理
对于任意命题公式,都存在与其等价的析取范式和合取范式。
例如
求公式 (P → ¬Q) ∨ (P ↔ R) 的析取范式和合取范式。
原式
= (¬P ∨ ¬Q) ∨ ((¬P ∨ R) ∧ (¬R ∨ P))
= ((¬P ∨ ¬Q) ∨ (¬P ∨ R)) ∧ ((¬P ∨ ¬Q) ∨ (¬R ∨ P))
= (¬P ∨ ¬Q ∨ ¬P ∨ R) ∧ (¬P ∨ ¬Q ∨ ¬R ∨ P)
= ((¬P ∨ ¬P) ∨ ¬Q ∨ R) ∧ ((¬P ∨ P) ∨ ¬Q ∨ ¬R)
= (¬P ∨ ¬Q ∨ R) ∧ (1 ∨ ¬Q ∨ ¬R)
= (¬P ∨ ¬Q ∨ R) ∧ 1
= (¬P ∨ ¬Q ∨ R) —合取范式
= ¬P ∨ ¬Q ∨ R —析取范式
小结
- 命题公式的析取范式可以指出公式何时为真,而合取范式可以指出公式何时为假,从而能够替代真值表
- 命题公式的范式表达并不唯一
- 一般而言,求解范式时,需要进行最后的化简步骤
2.8 主析取范式和主合取范式
2.8.1 极小项和极大项的定义和编码
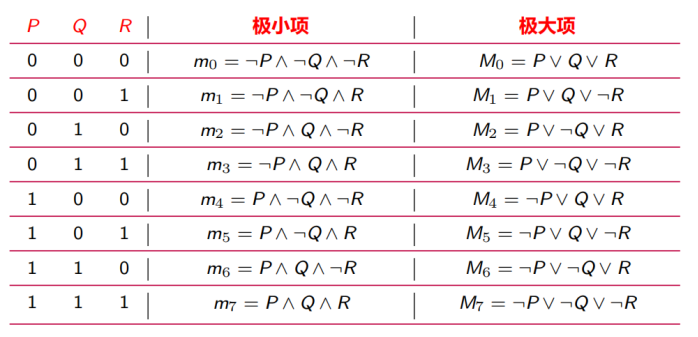
在含有 n 个命题变元 P1, P2, P3, · · · , Pn 的短语或子句中,若每个命题变元与其否定不同时存在,但二者之一恰好出现一次且仅一次,并且出现的次序与 P1, P2, P3, · · · , Pn 一致,则称此短语或子句为关于 P1, P2, P3, · · · , Pn 的一个极小项或极大项。
一般来说,若有 n 个命题变元,则应有 2^n 个不同的极小项和 2^n 个不同的极大项

- 没有两个不同的极小项是等价的。
- 每个极小项只有一组成真赋值,因此可用于给极小项编码。编码规律为:命题变元与 1 对应,命题变元的否定与 0 对应。
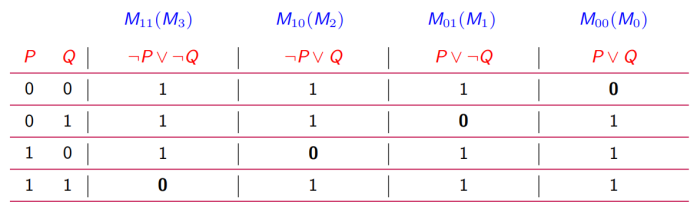
- 没有两个不同的极大项是等价的。
- 每个极大项只有一组成假赋值,因此可用于给极大项编码。编码规律为:命题变元与 0 对应,命题变元的否定与 1 对应。
注意:极小项和极大项的编码方式刚好相反,不要混淆。
举例
设有 P, Q, R 三个命题变元,给出以下极小项和极大项的编码:
- ¬P ∧ Q ∧ R: m011(m3)
- P ∧ ¬Q ∧ R: m101(m5)
- ¬P ∨ Q ∨ R: M100(M4)
- P ∨ ¬Q ∨ R: M010(M2)
根据编码给出相应的极小项或极大项:
- m6 = m110 = P ∧ Q ∧ ¬R
- M6 = M110 = ¬P ∨ ¬Q ∨ R
2.8.2 极小项和极大项的性质
- mi ∧ mj = 0 ;Mi ∨ Mj = 1 (i ≠ j)
- mi = ¬Mi ;Mi = ¬mi
2.8.3 主析取范式和主合取范式的定义
- 在给定的析取范式中,若每一个短语都是极小项,且按照编码从小到大的顺序排列,则称该范式为主析取范式(principal disjunctive normal form)。
- 在给定的合取范式中,若每一个子句都是极大项,且按照编码从小到大的顺序排列,则称该范式为主合取范式(principal conjunctive normal form)。
- 如果一个主析取范式不包含任何极小项,则称该主析取范式为 “空”;如果一个主合取范式不包含任何极大项,则称主合取范式为 “空”。
任何一个公式都有与之等价的主析取范式和主合取范式。
2.8.4 主范式求解定理
- 求出该公式所对应的析取范式和合取范式;
- 消去重复出现的命题变元,矛盾式或重言式;
E1 : G ∨ G = G; E2 : G ∧ G = G. (幂等律) E15 : ¬G ∧ G = 0. (矛盾律)
E7 : G ∨ 0 = G; E8 : G ∧ 1 = G.(同一律) E16 : ¬G ∨ G = 1. (排中律)
E9 : G ∨ 1 = 1; E10 : G ∧ 0 = 0.(零律)
- 若析取(合取)范式的某一个短语(子句)Bi 中缺少命题变元 P,则可用如下方式将 P 补进去:
Bi = Bi ∧ 1 = Bi ∧ (¬P ∨ P) = (Bi ∧ ¬P) ∨ (Bi ∧ P);
Bi = Bi ∨ 0 = Bi ∨ (¬P ∧ P) = (Bi ∨ ¬P) ∧ (Bi ∨ P)。
重复至所有短语或子句都是标准的极小项或极大项为止。
- 利用幂等律将重复的极小项和极大项合并,并利用交换律进行顺序调整,由此可转换成标准的主析取范式和主合取范式。
E1 : G ∨ G = G
E2 : G ∧ G = G. (幂等律)
E3 : G ∨ H = H ∨ G
E4 : G ∧ H = H ∧ G.(交换律)
举例
求公式 (P → Q) → (Q ∧ R) 的主析取范式和主合取范式
- 先求主析取范式
原式
= ¬(¬P ∨ Q) ∨ (Q ∧ R)
= (P ∧ ¬Q) ∨ (Q ∧ R) —析取范式 左边缺R,右边缺P,故应补上
= (P ∧ ¬Q ∧ (¬R ∨ R)) ∨ ((¬P ∨ P) ∧ Q ∧ R)
= (P ∧ ¬Q ∧ ¬R) ∨ (P ∧ ¬Q ∧ R) ∨ (¬P ∧ Q ∧ R) ∨ (P ∧ Q ∧ R)
= (¬P ∧ Q ∧ R) ∨ (P ∧ ¬Q ∧ ¬R) ∨ (P ∧ ¬Q ∧ R) ∨ (P ∧ Q ∧ R)
= m3∨m4∨m5∨m7
- 再求主合取范式
原式
= (P ∧ ¬Q) ∨ (Q ∧ R)
= (P ∨ Q) ∧ (P ∨ R) ∧ (¬Q ∨ Q) ∧ (¬Q ∨ R)
= (P ∨ Q) ∧ (P ∨ R) ∧ (¬Q ∨ R) –合取范式
= (P ∨ Q ∨ (¬R ∧ R)) ∧ (P ∨ (¬Q ∧ Q) ∨ R) ∧ ((¬P ∧ P) ∨ ¬Q ∨ R)
= (P ∨ Q ∨ ¬R) ∧ (P ∨ Q ∨ R) ∧ (P ∨ ¬Q ∨ R) ∧ (P∨Q∨R)∧(¬P∨¬Q∨R) ∧ (P∨¬Q∨R)
= (P ∨ Q ∨ ¬R) ∧ (P ∨ Q ∨ R) ∧ (P ∨ ¬Q ∨ R) ∧ (¬P ∨ ¬Q ∨ R)
= (P ∨ Q ∨ R) ∧ (P ∨ Q ∨ ¬R) ∧ (P ∨ ¬Q ∨ R) ∧ (¬P ∨ ¬Q ∨ R)
= M0 ∧ M1 ∧ M2 ∧ M6
2.8.5 真值表技术
利用真值表技术求主析取范式和主合取范式的简要方法:
列出真值表,选出公式的真值结果为真的所有的行,在这样的每一行中,找到其每一个解释所对应的极小项,将这些极小项进行析取即可得到相应的主析取范式。
列出真值表,选出公式的真值结果为假的所有的行,在这样的每一行中,找到其每一个解释所对应的极大项,将这些极大项进行合取即可得到相应的主合取范式。
从真值表按所给的算法求出主范式的方法,称为真值表技术 (technique of truth table)
举例
求公式 G = ¬(P → Q) ∨ R 的主析取范式和主合取范式
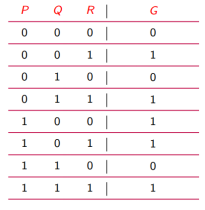
- 选出真值为真的行:第2,4,5,6,8 行,对应极小项m1, m3, m4, m5, m7,这些极小项构成了该公式的主析取范式
- 选出真值为假的行:第 1,3,7 行,对应极大项M0, M2, M6,这些极大项构成了该公式的主合取范式
2.8.6 范式的相互转化
由真值表技术可知,对于任一个命题公式而言,主析取范式所使用的极小项的编码和主合取范式所使用的极大项的编码是 “互补” 的关系。从而我们在求主析取范式和主合取范式时,可根据公式特点,先求出二者之一,然后可直接写出另一个。
例如,G(P,Q,R)= m0∨m1∨m3∨m4∨m6∨m7 = M2∧M5
2.8.7 主范式的应用
主范式可用于了解公式的真值情况,进行公式类型的判定以及等价关系的判定。
- 如果主析取范式包含所有的极小项,则该公式为永真公式;
- 如果主合取范式包含所有的极大项,则该公式为永假公式;
- 若两个公式具有相同的主析取范式或主合取范式,则两公式等价。
例
某研究所要从 A, B, C 三名科研骨干中挑选 1-2 名出国进修人员,由于工作需要,选派时要满足以下条件:
- 若A 去,则 C 同去;
- 若 B 去,则 C 不能去;
- 若 C 不能去,则 A 或 B 可以去。
问该如何选派?
解:
设P:派A去;Q:派B去;R:派C去,
则已知条件表示为:(P →R) ∧ (Q → ¬R) ∧ (¬R → (P ∨ Q)).
求出公式的主析取范式:
G
= (P → R) ∧ (Q → ¬R) ∧ (¬R → (P ∨ Q))
= (¬P ∨ R) ∧ (¬Q ∨ ¬R) ∧ (R ∨ (P ∨ Q))
= ((¬P ∧ ¬Q) ∨ (¬P ∧ ¬R) ∨ (¬Q ∧ R)) ∧ (P ∨ Q ∨ R)
= (¬P ∧ ¬Q ∧ R) ∨ (¬P ∧ Q ∧ ¬R) ∨ (P ∧ ¬Q ∧ R)
可见,有三种选派方案:
- C 去,A, B 都不去
- B 去,A, C 都不去
- A, C 同去,B 不去
2.9 基本推理形式和蕴涵公式
2.9.1 推理的基本形式
设G1, G2, · · · ,Gn, H是公式,称H 是G1,G2, · · · , Gn的逻辑结果,当且仅当对任意解释 I,如果I使得G1 ∧ G2 ∧ · · · ∧ Gn为真,则I也会使H为真。记为G1, G2, · · · ,Gn ⇒ H。“⇒”称为蕴涵关系。此时称 G1, G2, · · · , Gn ⇒ H 为有效的, 否则称为无效的。G1, G2, · · · , Gn称为一组前提,有时用集合 Γ 来表示,记为 Γ = {G1, G2, · · · ,Gn},H 称为结论。此时也称 H 是前提集合 Γ 的逻辑结果。记为 Γ ⇒ H。
2.9.2 推理的判定定理及判定方法
公式 H 是前提集合 Γ = {G1, G2, · · · , Gn} 的逻辑结果当且仅当 (G1 ∧ G2 ∧ · · · ∧ Gn) → H为永真公式
判定方法
- 真值表技术
- 公式转换法
- 主析取范式法
举例
判断推理 P → Q, P ⇒ Q 是否有效?
方法一:真值表技术
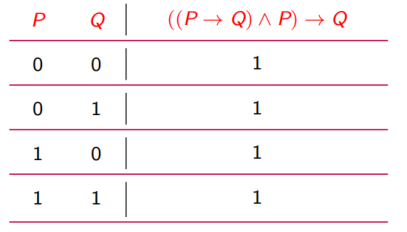
方法二:公式转换法
((P → Q) ∧ P) → Q
= ¬((¬P ∨ Q) ∧ P) ∨ Q
= ¬(¬P ∨ Q) ∨ ¬P ∨ Q
= ¬(¬P ∨ Q) ∨ (¬P ∨ Q)
= 1
方法三:主析取范式法
((P → Q) ∧ P) → Q
= ¬((¬P ∨ Q) ∧ P) ∨ Q = ¬(¬P ∨ Q) ∨ ¬P ∨ Q
= (P ∧ ¬Q) ∨ ¬P ∨ Q
= (P ∧ ¬Q) ∨ (¬P ∧ (¬Q ∨ Q)) ∨ ((¬P ∨ P) ∧ Q)
= (¬P ∧ ¬Q) ∨ (¬P ∧ Q) ∨ (P ∧ ¬Q) ∨ (P ∧ Q)
= (m0 ∨ m1 ∨ m2 ∨ m3)
2.9.3 推理定律–基本蕴涵关系
设 G, H, I 为任意的命题公式。
- G ∧ H ⇒ G ; G ∧ H ⇒ H. (简化规则)
- G ⇒ G ∨ H ;H ⇒ G ∨ H. (添加规则)
- G, H ⇒ G ∧ H (合取引入规则)
- G ∨ H, ¬G ⇒ H ;G ∨ H,¬H ⇒ G. (选言三段论)
- G → H, G ⇒ H (假言推理规则)
- G → H, ¬H ⇒ ¬G; (否定后件式)
- G → H, H → I ⇒ G → I (假言三段论)
- G ∨ H,G → I, H → I ⇒ I (二难推论)
2.10 自然演绎法推理
2.10.1 推理规则
- 规则P (前提引用规则):在推导的过程中,可随时引入前提集合中的任意一个前提;
- 规则T (逻辑结果引用规则):在推导的过程中,可以随时引入公式 S,该公式 S 是由其前的一个或多个公式推导出来的逻辑结果。
- 规则CP (附加前提规则):如果能从给定的前提集合 Γ 与公式 P 推导出 S,则能从此前提集合 Γ 推导出 P → S。
关于规则 CP
原理:P → (Q → R) = (P ∧ Q) → R。
使用场合: 当结论公式是蕴涵式或析取式时使用
2.10.2 自然演绎法
从前提集合 Γ 推出结论 H 的一个演绎是构造命题公式的一个有限序列:
H1, H2, H3, · · · , Hn−1, Hn
其中,Hi 或者是 Γ 中的某个前提,或者是前面的某些 Hj(j < i) 的有效结论,并且 Hn 就是 H,则称公式 H 为该演绎的有效结论,或者称从前提 Γ 能够演绎出结论 H 来。
2.10.3 直接证明法
设前提集合 Γ = {P ∨ Q, Q → R, P → S, ¬S},结论 H = R ∧ (P ∨ Q)。
证明 Γ ⇒ H。
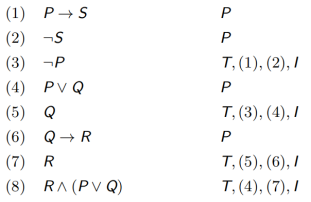
2.10.4 规则 CP 证明法
设前提集合 Γ = {P → (Q → S),¬R ∨ P, Q},结论 H = R → S。
证明 Γ ⇒ H。

2.10.5 间接证明法(反证法,归谬法)
- 要证明:G1, G2, · · · ,Gn ⇒ H
- 根据判定定理:(G1 ∧ G2 ∧ · · · ∧ Gn) → H 为永真公式
- 即:G1 ∧ G2 ∧ · · · ∧ Gn ∧ ¬H 是矛盾式
- 因此:G1 ∧ G2 ∧ · · · ∧ Gn ∧ ¬H ⇒ R ∧ ¬R
设前提集合 Γ = {P ∨ Q, P → R, Q → R},结论 H = R。
证明 Γ ⇒ H。

2.10.6 推理的应用
符号化下面的语句,并使用演绎法证明:
“若数 a 是实数,则它不是有理数就是无理数。若 a 不能表示成分数,则它不是有理数。a 是实数且它不能表示成分数。所以,a 是无理数。”
解
设命题
P : a 是实数;
Q : a 是有理数;
R : a 是无理数;
S : a 能表示成分数.
则推理符号化成:
P → (Q ∨ R), ¬S → ¬Q, P ∧ ¬S ⇒ R

![[附源码]Python计算机毕业设计jspm计算机学院党员积分管理系统](https://img-blog.csdnimg.cn/9f0a1c15c3534d3e9ba0b0c6e9c07f0b.png)
![[附源码]java毕业设计柠檬电动车租赁系统](https://img-blog.csdnimg.cn/afe6f10e98eb4cc1964a16a52a08e940.png)