【BBuf的CUDA笔记】十四，OpenAI Triton入门笔记三 FusedAttention

0x0. 前言

继续Triton的学习，这次来到 https://triton-lang.org/main/getting-started/tutorials/06-fused-attention.html 教程。也就是如何使用Triton来实现FlashAttention V2。对于FlashAttention和FlashAttention V2网上已经有非常多的介绍了，大家如果感兴趣的话我推荐FlashAttention V1看《图解大模型计算加速系列：FlashAttention V1，从硬件到计算逻辑》https://zhuanlan.zhihu.com/p/669926191 这篇文章的讲解以及 FlashAttention V2 看《图解大模型计算加速系列：Flash Attention V2，从原理到并行计算》 https://mp.weixin.qq.com/s/5K6yNj23NmNLcAQofHcT4Q ，原理和公式推导都非常清晰，不过想一口气读完还是要花一些精力的。同时你也可以在 https://github.com/BBuf/how-to-optim-algorithm-in-cuda 找到更多相关资料（此外Meagtron-LM，DeepSpeed等训练Infra框架的迅速跟进也说明了FlashAttention这个系列工作影响之大），例如：

在这里插入图片描述

这篇文章主要的问题是读懂如何使用Triton来实现FlashAttention V2的前向，所以我不会去复述FlashAttention的公式细节，而是从更加工程的角度来说FlashAttention Forward的代码应该如何实现，我在这个过程中也会提供FlashAttention V1/V2 Forward的一个最简Python实现来非常直观的把握代码流程，在这个基础上才会展开对Triton FlashAttention实现的解读，让我们开始吧。（后续如果有精力也会写一下Backward的实现

FlashAttention V1/V2的paper链接为：https://arxiv.org/abs/2205.14135 和 https://tridao.me/publications/flash2/flash2.pdf 。
本文涉及到的实验代码见我的个人仓库：https://github.com/BBuf/how-to-optim-algorithm-in-cuda/tree/master/triton ，也欢迎大家点star。

0x1. BenchMark

跑了一下 https://triton-lang.org/main/getting-started/tutorials/06-fused-attention.html 这个教程里的FlashAttention V2的BenchMark。

对于Batch=4，Head=48，HeadDim=64，causal=True的Flash Attention V2 Forward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

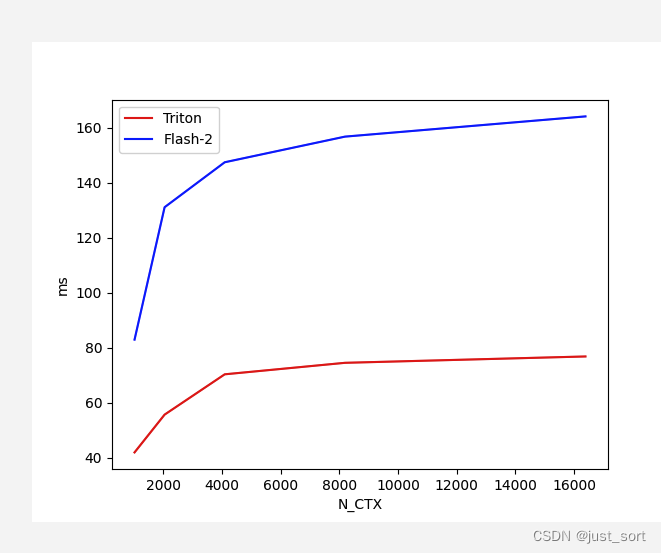
在这里插入图片描述

对于Batch=4，Head=48，HeadDim=64，causal=False的Flash Attention V2 Forward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

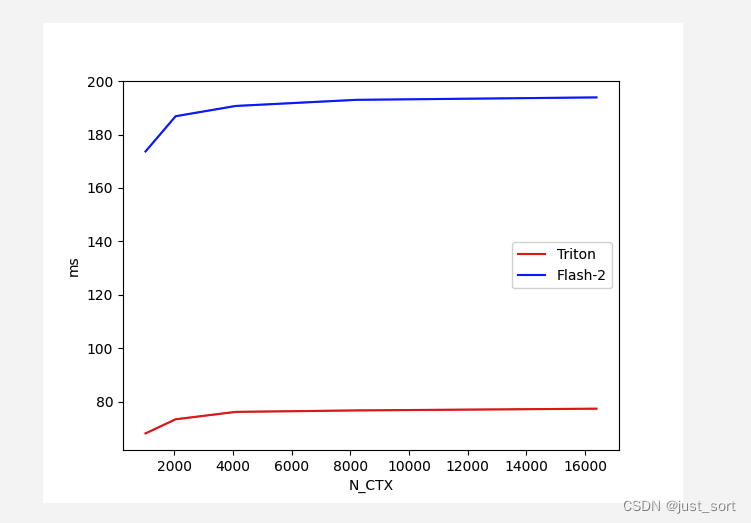
在这里插入图片描述

对于Batch=4，Head=48，HeadDim=64，causal=True的Flash Attention V2 Backward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

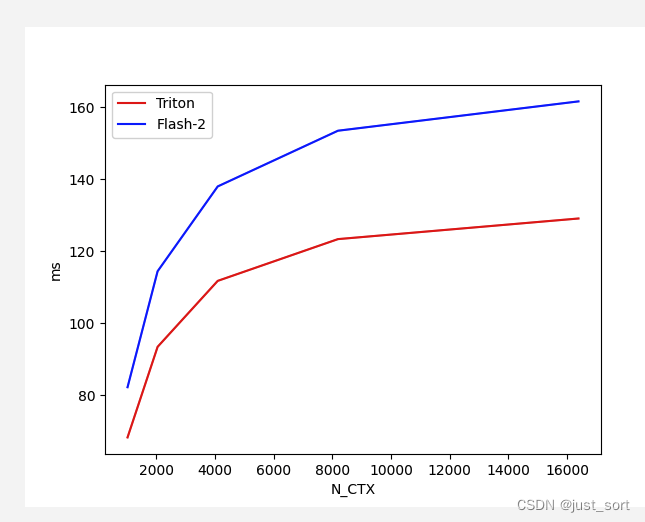
在这里插入图片描述

在这组配置下Triton在各种Sequence Length下都实现了比cutlass更优的性能，然后在Triton的kernel实现里面有assert Lk in {16, 32, 64, 128}，也就是说Triton的实现需要注意力头的隐藏层维度在[16, 32, 64, 128]里，我这里再测一组16的看下表现。

对于Batch=4，Head=48，HeadDim=16，causal=True的Flash Attention V2 Forward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

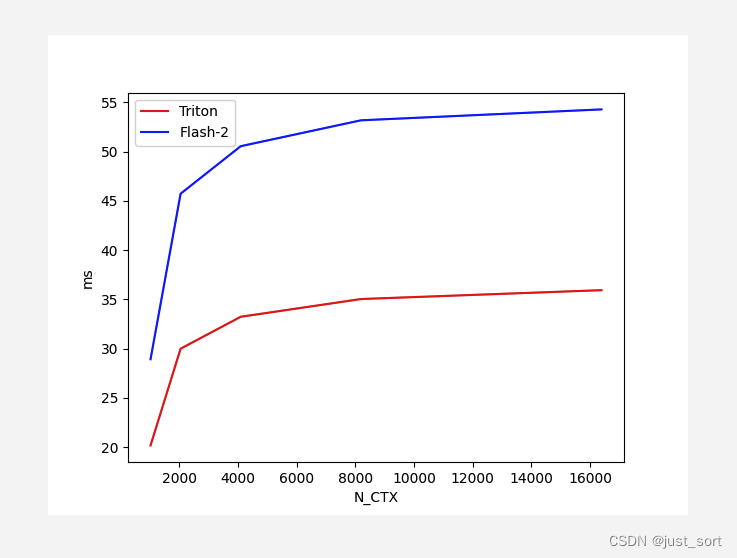
在这里插入图片描述

对于Batch=4，Head=48，HeadDim=16，causal=False的Flash Attention V2 Forward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

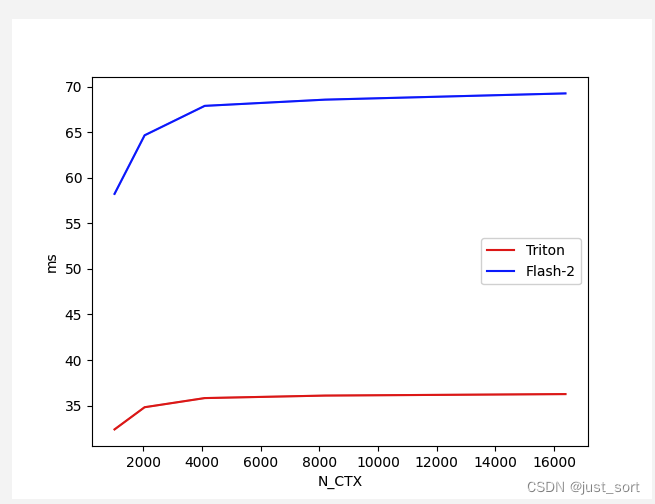
在这里插入图片描述

对于Batch=4，Head=48，HeadDim=16，causal=True的Flash Attention V2 Backward，对比不同序列长度下Triton实现和cutlass实现版本的性能：

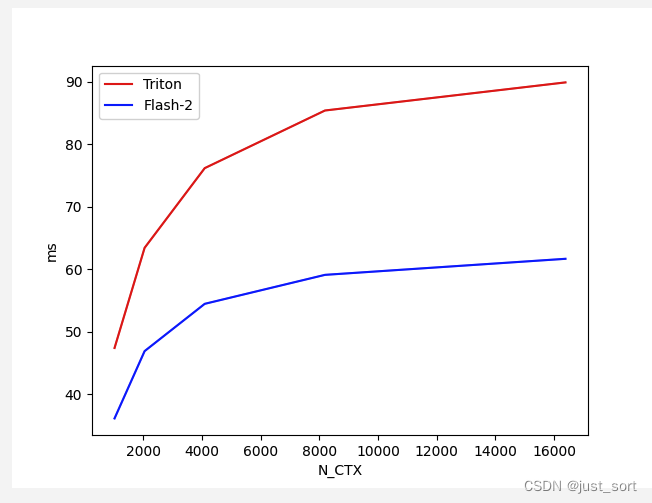
在这里插入图片描述

这一组case下虽然Forward Pass还是Triton更快，但是Backward Pass却是cutlass更快了。

另外之前在Triton的issue里面还刷如果HeadDim=128，Triton的Bakcward会比cutlass慢更多：https://github.com/openai/triton/issues/1975 ，参数设置为 BATCH, N_HEADS, N_CTX, D_HEAD = 8, 32, 4096, 128 这里也测试一下：

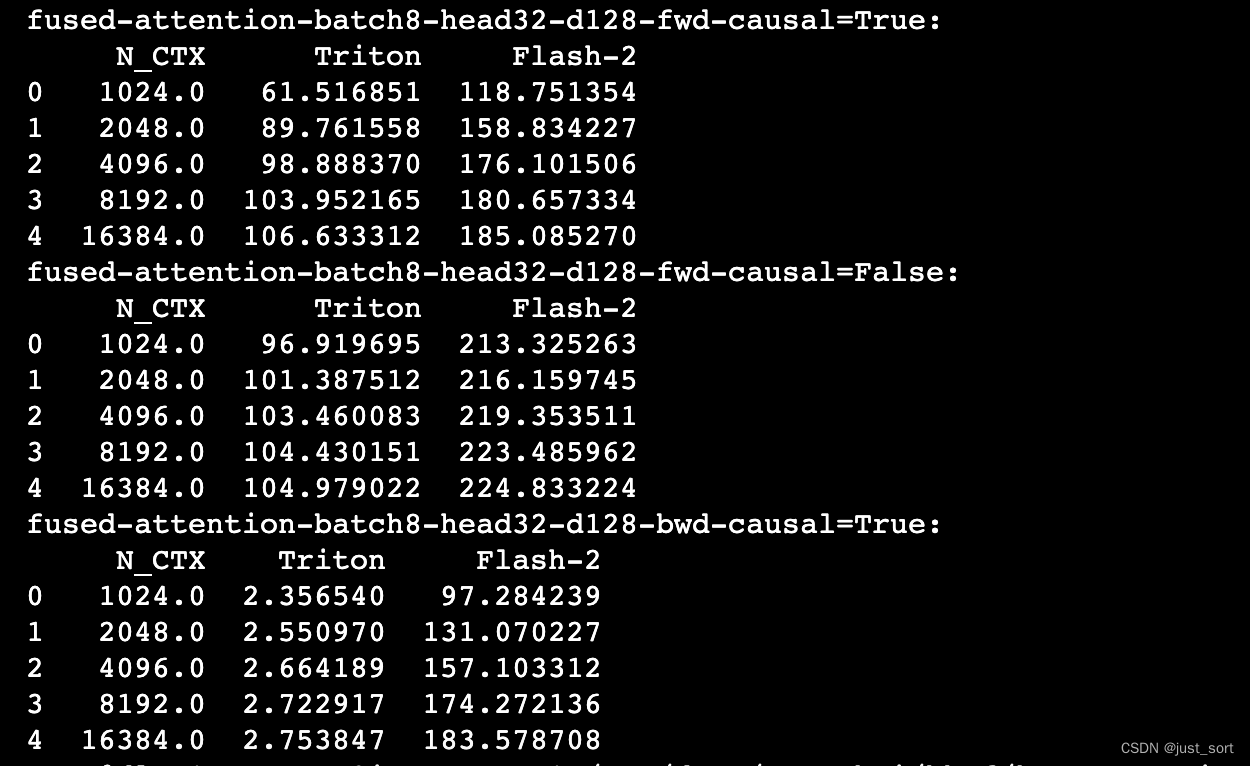
在这里插入图片描述

反向的耗时对比图：

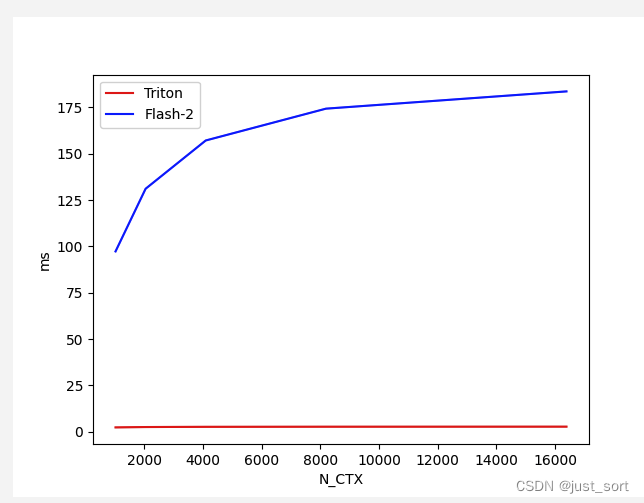
在这里插入图片描述

结果很神奇，这个反向耗时的差距非常大，且Triton的速度远好于Cutlass的实现，并且随着序列长度的增加Triton的反向的耗时竟然是接近横定的。。保险起见还是建议大家用官方FlashAttention库提供的实现，我现在使用的Triton版本为2.1.0。

0x2. 标准Attention流程以及Python极简实现

从FlashAttention的paper里面截一下标准Attention流程：

在这里插入图片描述

我这里再描述一下流程，首先从HBM中加载 $Q, K$ , $V$ 矩阵，接着执行 $S=QK^T$ 的计算，并将结果 $S$ 写回HBM；然后将 $S$ 再从HBM中读取出来，执行 $P = so f t ma x (S)$ 的计算，再将 $P$ 写回HBM；然后将 $P$ 和 $V$ 从HBM中读取出来，执行 $O = P V$ 的计算，最后把结果写回HBM中。对于， $Q, K, V, O$ ，他们的维度都是 $N\times d$ ，中间变量 $S$ 和 $P$ 的维度都是 $N\times N$ 。这里还有个问题就是对于S和P可能还会有一些其它的操作比如Mask和Dropout，所以上面也提到了有不少的fuse kernel的工作，比如把softmax和mask fuse起来。最后，这里的softmax是PyTorch的softmax算子，也是safe softmax的实现，safe的意思就是在naive softmac的基础上对指数上的每个原始输入值都减掉所有原始输入值中的最大值。具体请参考下面的图片，来源于 https://arxiv.org/pdf/2205.14135.pdf ：

在这里插入图片描述

对于safe softmax来说，所有的值都减掉了输入向量里面的最大值，保证了指数部分的最大值是0，避免了数值溢出。

为了验证正确性，我写了一个脚本，这个地方以经典的GPT2为例，然后硬件以A100为例。这里的 $N$ 和 $d$ 分别设置成1024和64，那么Q，K，V的shape都是 $(N, d) = (1024, 64)$ ，S和P的维度都是 $(N, N)$ 。

代码实现具体如下：

import torch

N, d = 1024, 64  # 更新N和d的值

Q_mat = torch.rand((N, d))
K_mat = torch.rand((N, d))
V_mat = torch.rand((N, d))

def standard_softmax_attention(Q, K, V):
    """
    执行标准的pytorch softmax和attention计算。
    """
    expected_softmax = torch.softmax(Q @ K.T, dim=1)
    expected_attention = expected_softmax @ V
    return expected_softmax, expected_attention

def safe_softmax_attention(Q, K, V):
    """
    执行安全的softmax和attention计算。
    """
    S_mat = Q @ K.T
    row_max = torch.max(S_mat, dim=1).values[:, None]
    input_safe = S_mat - row_max
    softmax_numerator = torch.exp(input_safe)
    softmax_denominator = torch.sum(softmax_numerator, dim=1)[:, None]
    safe_softmax = softmax_numerator / softmax_denominator
    matmul_result = safe_softmax @ V
    return safe_softmax, matmul_result

# 使用标准softmax和attention计算
expected_softmax, expected_attention = standard_softmax_attention(Q_mat, K_mat, V_mat)
# 使用安全softmax和attention计算
safe_softmax, safe_attention = safe_softmax_attention(Q_mat, K_mat, V_mat)

# 断言两种方法计算的softmax和attention结果是否接近
assert torch.allclose(safe_softmax, expected_softmax), "error in safe softmax"
assert torch.allclose(safe_attention, expected_attention), "error in safe attention"

测试可以正确通过，也说明了PyTorch的torch.softmax算子的确是用safe softmax的方法来实现的。

0x3. FlashAttention V1 Forward Pass以及Python极简实现

FlashAttention V1通过分块计算的方法，将Q、K和V切块成很多小块，然后将这些切分后的小块放进SRAM（shared memory）中执行计算，最后再写回HBM中。算法流程如下：

在这里插入图片描述

如果你想完全搞清楚这个伪代码的来龙去脉推荐看 https://zhuanlan.zhihu.com/p/669926191 这篇文章，但是从源码实现的角度来看，有了这个伪代码已经接近够了。只需要知道这些看似奇奇怪怪的公式是因为在分块遍历的时候每次计算的是一部分token，而自注意力机制要计算的最终结果是所有token间的，所以从局部到整体的更新就会用到在线的softmax算法以及在线更新最后的输出。这也是上面那堆复杂的公式由来。

我这里尝试用Python来模拟一下这个算法的流程，实现之后对Triton的实现会有帮助，因为从前面几节Triton的教程来看，相比于单纯的Python实现Triton kernel只是多了一个块级别的kernel启动过程而已。沿用上一节GPT2的设置， $N$ 和 $d$ 分别设置成1024和64，那么Q，K，V的shape都是 $(N, d) = (1024, 64)$ ，注意在FlashAttention里面就没有全局的S和P了。假设硬件是A100，A100的Shared Memory大小为192KB=196608B，那么可以计算出这里Flash Attention的分块大小，也就是上面的伪代码的第一行。

$B_c=M/4/64=768$ ， $B_r=min(768, 64)=64$ 。

然后伪代码的第2行初始化了一个全0的输出矩阵 $O$ ，shape的大小也是 $(N, d) = (1024, 64)$ ，同时初始化了一个 $l$ 和 $m$ 矩阵，维度大小都是 $(N)$ ，不过 $l$ 被初始化为全0矩阵， $m$ 被初始化为负无穷大。

接下来可以根据上面的参数直接计算出 $T_r$ 和 $T_c$ ，对应伪代码的第3行， $T_r=向上取整(N/B_r)=1024/64=16$ ， $T_c=向上取整(N/B_c)=1024/768=2$ 。

接下来的伪代码解析我直接放到下面的Python实现里，每一行代码都可以对应到上面的伪代码：

import torch

N, d = 1024, 64  # 更新N和d的值

Q_mat = torch.rand((N, d))
K_mat = torch.rand((N, d))
V_mat = torch.rand((N, d))

def standard_softmax_attention(Q, K, V):
    """
    执行标准的pytorch softmax和attention计算。
    """
    expected_softmax = torch.softmax(Q @ K.T, dim=1)
    expected_attention = expected_softmax @ V
    return expected_softmax, expected_attention

def flash_attention(Q, K, V, B_r=64, B_c=768):
    """
    使用分块计算和在线softmax校正执行flash attention算法。
    """
    O = torch.zeros((N, d))  # 初始化输出矩阵，对应伪代码的第2行
    l = torch.zeros((N, 1))  # 存储softmax分母，对应伪代码的第2行
    m = torch.full((N, 1), -torch.inf)  # 存储每个block的最大值，对应伪代码的第2行

    # 对应伪代码的第5行，for 1<=j<=T_c，注意这里是把K, V分成了T_c=[N/B_c]块，每一块的大小是[B_c, d]这么大
    # 所以在python实现的时候就直接通过一个步长为B_c的循环来处理
    for j in range(0, N, B_c):
        # 下面三行就对应了伪代码的第6行，Load Kj, Vj from HBM to on-chip SRAM
        # 但是这里是单纯的 python 实现，我们不可能真的把这一块内存从HBM上放到SRAM上
        # 这里只是一个伪代码的逻辑说明，可以假装它做到了，因为在Triton里面真的可以在Python层做到。
        j_end = j + B_c
        Kj = K[j:j_end, :]
        Vj = V[j:j_end, :]

        # 对应伪代码的第7行，for 1<=i<T_r，注意这里是把Q分成了Tr=[N/B_r]块，每一块的大小是[B_r, d]这么大
        # 所以在python实现的时候就直接通过一个步长为B_r的循环来处理
        for i in range(0, N, B_r):
            i_end = i + B_r
            mi = m[i:i_end, :]
            li = l[i:i_end, :]
            Oi = O[i:i_end, :]
            Qi = Q[i:i_end, :]

            # 对应伪代码的第9行：on chip, compute Sij，Sij的形状是[B_r, B_c]
            Sij = Qi @ Kj.T
            # 对应伪代码的第10行
            mij_hat = torch.max(Sij, dim=1).values[:, None]
            pij_hat = torch.exp(Sij - mij_hat)
            lij_hat = torch.sum(pij_hat, dim=1)[:, None]

            # 对应伪代码的第11行求mi_new的操作，注意这里要对两个张量求整体的max，所以才有这个stack操作
            mi_new = torch.max(torch.column_stack([mi, mij_hat]), dim=1).values[:, None]
            # 对应伪代码的第11行求li_new的操作
            li_new = torch.exp(mi - mi_new) * li + torch.exp(mij_hat - mi_new) * lij_hat
            # 对应伪代码的第12行，更新O_i。这里容易有一个疑问，伪代码上有一个diag操作，为什么下面的实现忽略了
            # 这是因为这个diag是作用在vector上的，实际上是为了在伪代码上能对应上维度，而PyTorch的实现是自动
            # 支持张量广播机制的，所以这里可以直接计算。
            O_i = (li * torch.exp(mi - mi_new) * Oi / li_new) + (torch.exp(mij_hat - mi_new) * pij_hat / li_new) @ Vj

            # 对应伪代码的第13行，更新m_i，l_i，O_i。
            m[i:i_end, :] = mi_new
            l[i:i_end, :] = li_new
            O[i:i_end, :] = O_i

    return O

# 执行flash attention计算
flash_attention_output = flash_attention(Q_mat, K_mat, V_mat)

# 执行标准的pytorch softmax和attention计算
expected_softmax, expected_attention = standard_softmax_attention(Q_mat, K_mat, V_mat)

# 断言flash attention计算的结果与标准计算结果是否接近
assert torch.allclose(flash_attention_output, expected_attention), "error in flash attention calculation"

需要说明的是在上面的Attention Forward Pass流程中没有考虑到Dropout以及Mask的操作，如果考虑这两个操作整体的流程有一些变化，具体如Flash Attention V1的paper里的Algorithm2所示：

在这里插入图片描述

相比于Algorithm1，多了Mask和Dropout的操作，其它的没有变化。

0x4. FlashAttention V2 Forward Pass以及Python极简实现

如果你想很清晰的了解FlashAttention V2背后的改进原理请阅读《图解大模型计算加速系列：Flash Attention V2，从原理到并行计算》 https://mp.weixin.qq.com/s/5K6yNj23NmNLcAQofHcT4Q 。我这里只做一个简单的原理解析，重点是关注代码层面相比于FlashAttention V1 Forward Pass的变化，并基于FlashAttention V1的版本实现FlashAttention V2 Forward Pass。

有了上一节代码的铺垫，Flash Attention V1 Forward Pass其实可以抽象为下面的图（从上面的《图解大模型计算加速系列：Flash Attention V2，从原理到并行计算》文章copy来的）：

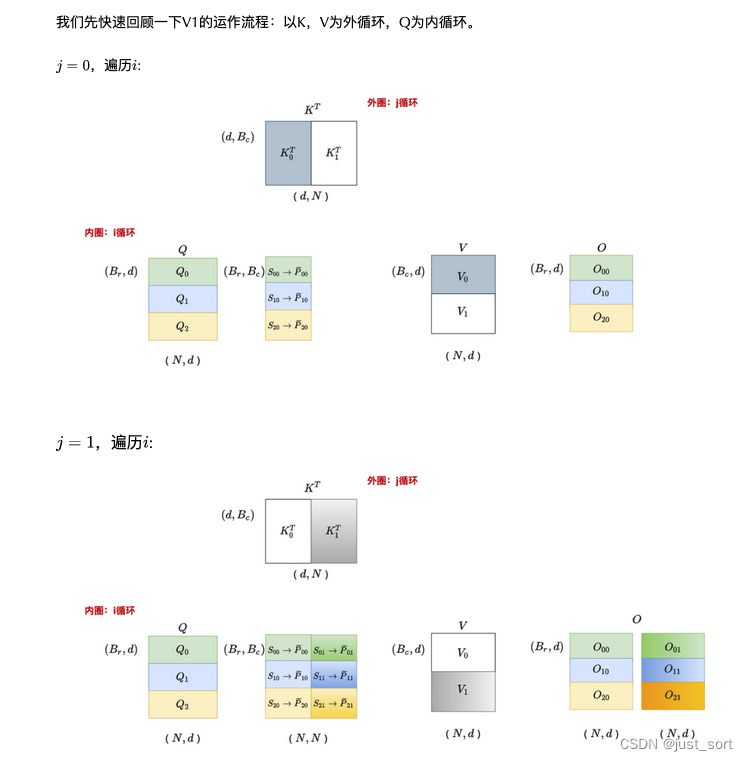
在这里插入图片描述

这个图和我们的Flash Attention V1实现是完全对应的，需要注意的是图中有6个O的小块，但实际上横着的O只有一个并且是逐步更新的，这里是为了体现分块的思想才画出来的。

这里以 $O_0$ 为例子，我们可以看到 $O_{00}$ 和 $O_{01}$ 共用了 $Q_0$ ，FlashAttention V2基于这个观察调整了Flash Attention V1的循环顺序，现在外层循环遍历Q不就可以避免重复访问Q了吗？调整训练的顺序只是FlashAttention V2的操作之一，另外两个比较重要的操作是对计算公式进行了改写尽量减少non-matmul FLOPs，具体来说在计算局部attention时，先不考虑softmax的分母以及将rescale的时机后移，只能感叹作者大佬的数学太强，具体的大家可以参考一下《FlashAttention2详解（性能比FlashAttention提升200%）》https://zhuanlan.zhihu.com/p/645376942 这篇文章的Algorthm的解释。此外，Paper中还提了一个重要的并行性方面的改进，即加入了序列并行，具体说来 FlashAttention V1 在 batch 和 heads 两个维度上进行了并行化，使用一个线程块来处理一个注意力头，总共需要的线程块的数量等于batch和注意力头的乘积。每个block被调到到一个SM上运行，例如A100 GPU上有108个SMs。当block数量很大时（例如≥80），这种调度方式是高效的，因为这几乎可以有效利用GPU上所有计算资源。但是在处理长序列输入（目前训练100k，200k的长文本模型需求逐步增长）时，由于内存限制，通常会减小batch和注意力头数量，这样GPU并行化程度就降低了。基于此，FlashAttention-2在序列长度这一维度上进行并行化，显著提升了GPU的并行度并提升了性能。这些改进我们都可以在 https://github.com/openai/triton/blob/main/python/tutorials/06-fused-attention.py 这个Triton实现中找到，留在下一节细讲。

这里仍然是贴出Flash AttentionV2的算法伪代码，并且使用Python来模拟一下流程。

在这里插入图片描述

对应的python代码以及流程如下，由于这里只考虑了forward pass所以代码里只计算了Attention的输出O没有计算logsumexp L（这个是给backward pass用的）：

import torch

N, d = 1024, 64  # 更新N和d的值

Q_mat = torch.rand((N, d))
K_mat = torch.rand((N, d))
V_mat = torch.rand((N, d))

def standard_softmax_attention(Q, K, V):
    """
    执行标准的PyTorch softmax和attention计算。
    """
    expected_softmax = torch.softmax(Q @ K.T, dim=1)
    expected_attention = expected_softmax @ V
    return expected_softmax, expected_attention

def flash_attention_v2(Q, K, V, B_r=64, B_c=768):
    """
    使用分块计算和在线softmax校正执行flash attention v2算法。
    """
    O = torch.zeros((N, d))  # 初始化O为(N, d)的形状，实际上对应伪代码第5行的O初始化
    l = torch.zeros((N, 1))  # 初始化l为(N)的形状，实际上对应伪代码第5行的l初始化
    m = torch.full((N, 1), -torch.inf)  # 存储每个block的最大值，初始化为负无穷大，对应伪代码的第5行

    # 对应伪代码的第3行，for 1<=i<T_r，注意这里是把Q分成了Tr=[N/B_r]块，每一块的大小是[B_r, d]这么大
    # 所以在python实现的时候就直接通过一个步长为B_r的循环来处理
    for i in range(0, N, B_r):
        Qi = Q[i:i+B_r, :]
        # 对应伪代码的第 6 行，for 1<=j<=T_c，注意这里是把K, V分成了T_c=[N/B_c]块，每一块的大小是[B_c, d]这么大
        # 所以在python实现的时候就直接通过一个步长为B_c的循环来处理 
        for j in range(0, N, B_c):  # 内循环遍历Q的块
            Kj = K[j:j+B_c, :]
            Vj = V[j:j+B_c, :]

            # 对应伪代码的第8行：on chip, compute Sij，Sij的形状是[B_r, B_c]
            Sij = Qi @ Kj.T
            # 对应伪代码的第9行求m_i^(j)的操作，mi_new的形状是B_r
            mi_new = torch.max(torch.column_stack([m[i:i+B_r], torch.max(Sij, dim=1).values[:, None]]), dim=1).values[:, None]
            # 对应伪代码的第9行求Pij_hat的操作，Pij_hat的形状是(B_r x B_c)，和Sij一致
            Pij_hat = torch.exp(Sij - mi_new)
            # 对应伪代码的第9行求lij的操作
            l[i:i+B_r] = torch.exp(m[i:i+B_r] - mi_new) * l[i:i+B_r] + torch.sum(Pij_hat, dim=1)[:, None]
            # 对应伪代码的第10行求O_ij的操作
            O[i:i+B_r] = O[i:i+B_r] * torch.exp(m[i:i+B_r] - mi_new) + Pij_hat @ Vj
            m[i:i+B_r] = mi_new

    O = O / l  # 对应伪代码第12行，根据softmax的分母校正输出
    return O

# 执行flash attention计算
flash_attention_v2_output = flash_attention_v2(Q_mat, K_mat, V_mat)

# 执行标准的PyTorch softmax和attention计算
_, expected_attention = standard_softmax_attention(Q_mat, K_mat, V_mat)

# 断言flash attention计算的结果与标准计算结果是否接近
assert torch.allclose(flash_attention_v2_output, expected_attention), "Error in flash attention calculation"

然后FlashAttention V2里面还有两节和GPU并行性相关的话，在对Triton实现的解读之前我先把这两节翻译一下。

在这里插入图片描述

翻译：FlashAttention V1在batch和heads两个维度上进行了并行化：使用一个thread block来处理一个attention head，总共需要thread block的数量等于batch size × number of heads。每个block被调到到一个SM上运行，例如A100 GPU上有108个SMs。当block数量很大时（例如≥80），这种调度方式是高效的，因为几乎可以有效利用GPU上所有计算资源。

但是在处理长序列输入时，由于内存限制，通常会减小batch size和head数量，这样并行化成都就降低了。因此，FlashAttention V2还在序列长度这一维度上进行并行化，显著提升了计算速度。此外，当batch size和head数量较小时，在序列长度上增加并行性有助于提高GPU占用率。

Forward pass 这里大概就是说，FlashAttention V1伪代码中有两个循环，K，V在外循环j，Q在内循环i。FlashAttention V2将Q移到了外循环i，K，V移到了内循环 j，由于改进了算法使得warps之间不再需要相互通信去处理，所以外循环可以放在不同的 thread block 上。这个交换的优化方法是由Phil Tillet在Triton提出并实现的，也就是下一节要解读的Triton代码了。我们会看到它启动kernel的时候线程网格有两个维度，其中一个维度是序列长度，另外一个维度是batch和注意力头数的乘积。

在这里插入图片描述

翻译：paper 的3.2节讨论了如何分配thread block，然而在每个thread block内部，我们也需要决定如何在不同的warp之间分配工作。我们通常在每个thread block中使用4或8个warp，如Figure3所示。

FlashAttention forward pass. 这里精简一下，如Figure3所示，外循环对K，V在输入序列N上遍历，内循环对Q在N上遍历。对于每个块，FlashAttention V1将K和V分别分成4个warp，并且所有的warp都可以访问Q。K的warp乘以Q得到S的一部分 $S_{ij}$ ，然后 $S_{ij}$ 经过局部softmax后还需要乘以V的一部分得到 $O_i$ 。但是，每次外循环 $j + +$ 都要更新一次 $O_i$ （对上一次的 $O_i$ 先rescale再加上当前的值），这就导致每个warp需要从HBM里面频繁读写 $O_i$ 来累计最后的结果，这种方案也被称为"Split-K"方案，整体是低效的，因为所有warp都需要从HBM频繁读写中间结果 $Q_i, O_i, m_i, l_i)$ 。FlashAttention V2 将Q移到了外循环i，K，V移到了内循环j，并将Q分为4个warp，所有warp都可以访问K，V。这样做的好处是，原来FlashAttention每次内循环i++会导致 $O_i$ 也变换（而 $O_i$ 需要通过HBM读写），现在每次内循环j++处理的都是 $O_i$ ，此时 $O_i$ 是存储在SRAM上的，代价远小于HBM。

0x5. FlashAttention V2 Forward Pass Triton 实现解读

有了上面的铺垫，就可以直接来看Triton的实现了，这里只关注 Forward Pass部分，Triton的核心计算逻辑在下面的这个函数：

@triton.jit
def _attn_fwd_inner(acc, l_i, m_i, q,  #
                    K_block_ptr, V_block_ptr,  #
                    start_m, qk_scale,  #
                    BLOCK_M: tl.constexpr, BLOCK_DMODEL: tl.constexpr, BLOCK_N: tl.constexpr,  #
                    STAGE: tl.constexpr, offs_m: tl.constexpr, offs_n: tl.constexpr,  #
                    N_CTX: tl.constexpr):
    # range of values handled by this stage
    # 根据STAGE的值，函数定义了处理的键（K）和值（V）的范围。
    # 不同的STAGE对应不同的处理范围，支持因果（causal）和非因果（non-causal）的自注意力。
    if STAGE == 1: # causal = True
        lo, hi = 0, start_m * BLOCK_M
    elif STAGE == 2:
        lo, hi = start_m * BLOCK_M, (start_m + 1) * BLOCK_M
        lo = tl.multiple_of(lo, BLOCK_M)
    # causal = False
    else:
        lo, hi = 0, N_CTX
    # 使用tl.advance函数调整K和V指针的位置，以正确地从相应的内存位置加载数据。
    K_block_ptr = tl.advance(K_block_ptr, (0, lo))
    V_block_ptr = tl.advance(V_block_ptr, (lo, 0))
    # loop over k, v and update accumulator
    # 在一个循环中，函数加载键（K）的一个块，计算查询（Q）与这个键块的点积，
    # 然后根据当前STAGE调整计算结果。如果是STAGE 2并且因果关系为真，会应用一个掩码来屏蔽未来的信息。
    for start_n in range(lo, hi, BLOCK_N):
        start_n = tl.multiple_of(start_n, BLOCK_N)
        # -- compute qk ----
        k = tl.load(K_block_ptr)
        qk = tl.zeros([BLOCK_M, BLOCK_N], dtype=tl.float32)
        qk += tl.dot(q, k)
        if STAGE == 2:
            mask = offs_m[:, None] >= (start_n + offs_n[None, :])
            qk = qk * qk_scale + tl.where(mask, 0, -1.0e6)
            m_ij = tl.maximum(m_i, tl.max(qk, 1))
            qk -= m_ij[:, None]
        else:
            # 对应算法流程伪代码的第9行的m_ij的计算，和伪代码的区别是这里应用了qk_scale
            m_ij = tl.maximum(m_i, tl.max(qk, 1) * qk_scale)
            qk = qk * qk_scale - m_ij[:, None]
        # 计算p，对应伪代码的第9行的p的计算
        p = tl.math.exp2(qk)
        l_ij = tl.sum(p, 1)
        # -- update m_i and l_i
        alpha = tl.math.exp2(m_i - m_ij)
        l_i = l_i * alpha + l_ij
        # -- update output accumulator --
        acc = acc * alpha[:, None]
        # update acc
        v = tl.load(V_block_ptr)
        acc += tl.dot(p.to(tl.float16), v)
        # update m_i and l_i
        m_i = m_ij
        V_block_ptr = tl.advance(V_block_ptr, (BLOCK_N, 0))
        K_block_ptr = tl.advance(K_block_ptr, (0, BLOCK_N))
    return acc, l_i, m_i

需要说明的是这个_attn_fwd_inner函数负责的是一小块Q（入参中的q）和KV的计算，代码中的for循环对应的就是伪代码中的对KV的循环，而Q的循环实际上是体现在triton kernel启动的设置，见下面的代码和注释：

# 定义了一个_attention类，它继承自torch.autograd.Function。这允许我们自定义一个操作的前向和后向传播
#（即计算梯度的方式），使其能够与PyTorch的自动梯度计算系统无缝集成。
class _attention(torch.autograd.Function):

    @staticmethod
    # forward方法定义了这个自定义操作的前向传播逻辑。ctx是一个上下文对象，用于存储用于反向传播的信息。
    # q, k, v分别代表query, key, value三个输入Tensor，causal和sm_scale是额外的控制参数。
    def forward(ctx, q, k, v, causal, sm_scale):
        # shape constraints
        # 这几行代码检查输入Tensor的最后一个维度，确保它们的大小相等且为特定的值（16, 32, 64, 或 128）。这是由于实现的特定性能优化需要。
        Lq, Lk, Lv = q.shape[-1], k.shape[-1], v.shape[-1]
        assert Lq == Lk and Lk == Lv
        assert Lk in {16, 32, 64, 128}
        # 初始化一个与q相同形状和类型的空Tensoro，用于存储输出结果。
        o = torch.empty_like(q)
        # 这几行设置了几个关键的性能调优参数，包括处理块的大小（BLOCK_M, BLOCK_N）和
        # 计算阶段的数量（num_stages）。num_warps指的是每个CUDA block中warp的数量。
        BLOCK_M = 128
        BLOCK_N = 64 if Lk <= 64 else 32
        num_stages = 4 if Lk <= 64 else 3
        num_warps = 4
        stage = 3 if causal else 1
        # 根据CUDA设备的能力（这里检查的是计算能力9.x，即NVIDIA Volta架构及以后的架构），进一步调整num_warps和num_stages。
        # Tuning for H100
        if torch.cuda.get_device_capability()[0] == 9:
            num_warps = 8
            num_stages = 7 if Lk >= 64 else 3
        # 计算Triton kernel的网格尺寸。triton.cdiv是一个辅助函数，用于计算向上取整的除法。
        # q.shape[2]是序列长度，q.shape[0]和q.shape[1]分别是batch和seq length
        grid = (triton.cdiv(q.shape[2], BLOCK_M), q.shape[0] * q.shape[1], 1)
        # 初始化另一个TensorM，用于在计算过程中存储中间结果。
        M = torch.empty((q.shape[0], q.shape[1], q.shape[2]), device=q.device, dtype=torch.float32)
        # 调用Triton kernel _attn_fwd执行实际的attention计算。这里传递了大量的参数，包括输入Tensor的各个维度、步长（stride）、形状、调优参数等。
        _attn_fwd[grid](
            q, k, v, sm_scale, M, o,  #
            q.stride(0), q.stride(1), q.stride(2), q.stride(3),  #
            k.stride(0), k.stride(1), k.stride(2), k.stride(3),  #
            v.stride(0), v.stride(1), v.stride(2), v.stride(3),  #
            o.stride(0), o.stride(1), o.stride(2), o.stride(3),  #
            q.shape[0], q.shape[1],  #
            N_CTX=q.shape[2],  #
            BLOCK_M=BLOCK_M,  #
            BLOCK_N=BLOCK_N,  #
            BLOCK_DMODEL=Lk,  #
            STAGE=stage,  #
            num_warps=num_warps,  #
            num_stages=num_stages  #
        )

这里的triton.cdiv(q.shape[2], BLOCK_M)其实就是对Q进行分块，需要说明的是这个地方输入的Q，K，V的形状是(Batch, NHeads, Seq, HeadDim)，所以这里启动的线程网格有2个维度都是有值的，除了x维度为triton.cdiv(q.shape[2], BLOCK_M)，它的y维度则为q.shape[0] * q.shape[1]的乘积（这里的x是在序列维度上切分也导致了后面构造内存指针的时候有一个特殊的order=(1, 0),参数）。也就是说这里的Block数量其实是比较多的，更容易让GPU的SM用满，这个启动方式和FlashAttention V2 paper中提到的启动方式是一致的，具体请看上一节的末尾翻译部分。至于，我们在计算的时候使用多少个warp，这个也是和Paper的设置保持一致，一般是用4个，只有针对H100才用8个。另外就是由于现在的Q，K，V形状和paper中的 $(N, d)$ 不一样，所以分块的个数也是不一样的，这里是写死了分块数：

BLOCK_M = 128
BLOCK_N = 64 if Lk <= 64 else 32

最后还有一个_attn_fwd要解析，内容如下：

@triton.jit
# 定义了一个名为_attn_fwd的函数。这个函数是实现注意力机制前向pass的kernel。函数参数包括输入的Query（Q）、Key（K）、Value（V）张量，
# softmax缩放因子（sm_scale），一个中间计算结果（M）和输出张量（Out），以及多个关于这些张量的步长（stride）参数和其他配置常量。
def _attn_fwd(Q, K, V, sm_scale, M, Out,  #
              stride_qz, stride_qh, stride_qm, stride_qk,  #
              stride_kz, stride_kh, stride_kn, stride_kk,  #
              stride_vz, stride_vh, stride_vk, stride_vn,  #
              stride_oz, stride_oh, stride_om, stride_on,  #
              Z, H,  #
              N_CTX: tl.constexpr,  #
              BLOCK_M: tl.constexpr,  #
              BLOCK_DMODEL: tl.constexpr,  #
              BLOCK_N: tl.constexpr,  #
              STAGE: tl.constexpr  #
              ):
    # 注意，输入参数里的Z和H分别表示batch size和注意力头数
    # start_m表示当前kernel program 实例对应的seq维度的偏移，而off_hz表示的是batch*heads维度的偏移。
    start_m = tl.program_id(0)
    off_hz = tl.program_id(1)

    # 这些行计算了两个偏移量off_z和off_h，它们分别代表在batch（或heads）中的位置。
    off_z = off_hz // H
    off_h = off_hz % H
    # 计算用于定位Q、K和V张量中当前处理块的偏移量。这是基于先前计算的偏移量和提供的步长参数。
    qvk_offset = off_z.to(tl.int64) * stride_qz + off_h.to(tl.int64) * stride_qh

    # block pointers
    # 使用tl.make_block_ptr创建一个指向Q张量当前处理块的指针。这个函数调用指定了基础地址、形状、步长、偏移量和块形状等，以及如何在内存中访问这个数据块。
    # N_CTX 是q.shape[2]，表示的是序列长度，BLOCK_DMODEL是Lk，表示的是每个注意力头的隐藏层维度大小
    # 下面几个make_block_ptr创建的张量类似，分别是对K，V以及输出O创建指向当前处理块的指针
    Q_block_ptr = tl.make_block_ptr(
        base=Q + qvk_offset,
        shape=(N_CTX, BLOCK_DMODEL),
        strides=(stride_qm, stride_qk),
        offsets=(start_m * BLOCK_M, 0),
        block_shape=(BLOCK_M, BLOCK_DMODEL),
        order=(1, 0),
    )
    V_block_ptr = tl.make_block_ptr(
        base=V + qvk_offset,
        shape=(N_CTX, BLOCK_DMODEL),
        strides=(stride_vk, stride_vn),
        offsets=(0, 0),
        block_shape=(BLOCK_N, BLOCK_DMODEL),
        order=(1, 0),
    )
    K_block_ptr = tl.make_block_ptr(
        base=K + qvk_offset,
        shape=(BLOCK_DMODEL, N_CTX),
        strides=(stride_kk, stride_kn),
        offsets=(0, 0),
        block_shape=(BLOCK_DMODEL, BLOCK_N),
        order=(0, 1),
    )
    O_block_ptr = tl.make_block_ptr(
        base=Out + qvk_offset,
        shape=(N_CTX, BLOCK_DMODEL),
        strides=(stride_om, stride_on),
        offsets=(start_m * BLOCK_M, 0),
        block_shape=(BLOCK_M, BLOCK_DMODEL),
        order=(1, 0),
    )
    # initialize offsets
    # 计算M维度（seq维度）上每个线程应处理的元素的起始偏移量。
    offs_m = start_m * BLOCK_M + tl.arange(0, BLOCK_M)
    # 计算N维度（batch*heads维度）上每个线程应处理的元素的偏移量。
    offs_n = tl.arange(0, BLOCK_N)
    # initialize pointer to m and l
    # 初始化m向量，m用于存储每个m维度上的最大logit，初始化为负无穷大。
    m_i = tl.zeros([BLOCK_M], dtype=tl.float32) - float("inf")
    # 初始化l向量，l用于累计softmax的分母，初始化为1。
    l_i = tl.zeros([BLOCK_M], dtype=tl.float32) + 1.0
    # 初始化累加器，用于累积注意力加权和。注意这里的shape是(BLOCK_M, BLOCK_DMODEL)
    acc = tl.zeros([BLOCK_M, BLOCK_DMODEL], dtype=tl.float32)
    # load scales
    qk_scale = sm_scale     # 加载softmax缩放因子。
    qk_scale *= 1.44269504  # 将softmax缩放因子乘以1/log(2)，用于后续计算。
    # load q: it will stay in SRAM throughout
    q = tl.load(Q_block_ptr) # 将Q矩阵的当前块加载到SRAM中，此数据在整个计算过程中保持不变。
    # stage 1: off-band
    # For causal = True, STAGE = 3 and _attn_fwd_inner gets 1 as its STAGE
    # For causal = False, STAGE = 1, and _attn_fwd_inner gets 3 as its STAGE
    if STAGE & 1:
        acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr,  #
                                        start_m, qk_scale,  #
                                        BLOCK_M, BLOCK_DMODEL, BLOCK_N,  #
                                        4 - STAGE, offs_m, offs_n, N_CTX  #
                                        )
    # stage 2: on-band
    if STAGE & 2:
        # barrier makes it easier for compielr to schedule the
        # two loops independently
        tl.debug_barrier()
        acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr,  #
                                        start_m, qk_scale,  #
                                        BLOCK_M, BLOCK_DMODEL, BLOCK_N,  #
                                        2, offs_m, offs_n, N_CTX  #
                                        )
    # epilogue
    m_i += tl.math.log2(l_i)
    acc = acc / l_i[:, None]
    m_ptrs = M + off_hz * N_CTX + offs_m
    tl.store(m_ptrs, m_i)
    tl.store(O_block_ptr, acc.to(Out.type.element_ty))

需要特别注意的是这段代码最后的epilogue部分就对应了FlashAttention V2伪代码中的12行以后的内容，根据softmax的分母部分较正输出。此外，Triton的实现里面考虑了一些paper里面没有的东西比如qk_scale，causal mask，对Q*K的结果S应用了减掉m，使得整个实现看起来要复杂不少，但整体的算法逻辑和并行设置和paper还是一致的。