一、数据描述
数据来源2013年各地区水泥制造业规模以上企业的各主要经济指标,原始数据来源于2014年(《中国水泥统计年鉴》),试对用主成分和因子进行经济效益评价。
地区,企业个数(亿元),流动资产合计(亿元),资产总额(亿元),负债总额(亿元),主营业务收入(亿元),利润总额(亿元),销售利润率(%)
北京,8,17.6,43.8,17.8,26.6,-1.4,-5.2
天津,24,43.8,91.7,33.7,35.9,1.5,4.1
河北,231,281.4,993.8,647,565.1,22.7,4
山西,113,103.4,317.4,238.5,124,-2.1,-1.7
内蒙古,116,135.9,384.4,256.8,245.8,11.9,4.8
辽宁,151,151.4,417.6,247.9,350.3,23,6.6
吉林,69,333.7,627.7,415.2,539.8,25.4,4.7
黑龙江,96,142.1,331.6,234.7,183.2,13.5,7.4
上海,14,21.5,28.3,12.6,31.6,1.2,4
江苏,254,300.3,680,435.7,713.3,62.6,8.8
浙江,192,259.8,561.9,300.1,473.9,42.1,8.9
安徽,169,217.2,591.9,305.2,518.8,64.9,12.5
福建,111,93.2,276.4,163.9,284.8,11.2,3.9
江西,138,143.8,398.1,208.4,400.3,47.5,11.9
山东,295,351.8,792.7,412.5,878.3,80.3,9.1
河南,238,388.5,804.2,475.2,673.7,58.3,8.7
湖北,151,193,619.7,360.7,570.5,49.1,8.6
湖南,220,86.4,398.8,212.3,434.1,33.6,7.7
广东,204,217,592.1,345.3,474.3,40.5,8.5
广西,148,116,387.2,178.7,344,49.6,14.4
海南,15,53.1,102.1,52.9,80.7,5.6,6.9
重庆,78,158.3,419.8,294.1,185.1,8.4,4.5
四川,196,218.2,739.1,433.3,465.2,37.1,8
贵州,133,91.5,367.5,244.2,224.7,28.2,12.6
云南,149,134.2,434.7,290.2,251,11.3,4.5
西藏,10,11.3,26.5,5.4,17.4,4.1,23.7
陕西,116,82.2,312.6,203.8,253.2,14.4,5.7
甘肃,68,61.8,213.2,126.8,124.3,13.3,10.7
青海,20,39.5,152.7,123.1,44.4,3,6.7
宁夏,27,36.1,90.1,49.2,45.1,3.4,7.4
新疆,86,220.6,602.7,353.4,136.1,1.5,1.1
二、读入数据
df<-read.csv('f:/桌面/水泥制造企业.csv')attach(df)
attach(df)
names(df)<-c('areas','x1','x2','x3','x4','x5','x6','x7')
df
df
areas x1 x2 x3 x4 x5 x6 x7
1 北京 8 17.6 43.8 17.8 26.6 -1.4 -5.2
2 天津 24 43.8 91.7 33.7 35.9 1.5 4.1
3 河北 231 281.4 993.8 647.0 565.1 22.7 4.0
4 山西 113 103.4 317.4 238.5 124.0 -2.1 -1.7
5 内蒙古 116 135.9 384.4 256.8 245.8 11.9 4.8
6 辽宁 151 151.4 417.6 247.9 350.3 23.0 6.6
7 吉林 69 333.7 627.7 415.2 539.8 25.4 4.7
8 黑龙江 96 142.1 331.6 234.7 183.2 13.5 7.4
9 上海 14 21.5 28.3 12.6 31.6 1.2 4.0
10 江苏 254 300.3 680.0 435.7 713.3 62.6 8.8
11 浙江 192 259.8 561.9 300.1 473.9 42.1 8.9
12 安徽 169 217.2 591.9 305.2 518.8 64.9 12.5
13 福建 111 93.2 276.4 163.9 284.8 11.2 3.9
14 江西 138 143.8 398.1 208.4 400.3 47.5 11.9
15 山东 295 351.8 792.7 412.5 878.3 80.3 9.1
16 河南 238 388.5 804.2 475.2 673.7 58.3 8.7
...
三、对样本数据进行主成分分析
1.提取主成分
df.pr<-princomp(df[,c('x1','x2','x3','x4','x5','x6','x7')],cor=TRUE,scores=TRUE)
summary(df.pr,loadings = TRUE)
运行得到:
summary(df.pr,loadings = TRUE)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
Standard deviation 2.272309 1.099611 0.584717 0.4413558 0.22149843 0.18479654 0.08698225
Proportion of Variance 0.737627 0.172735 0.048842 0.0278278 0.00700879 0.00487854 0.00108084
Cumulative Proportion 0.737627 0.910362 0.959204 0.9870318 0.99404062 0.99891916 1.00000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
x1 0.407 0.340 0.681 0.478 0.151
x2 0.410 -0.155 -0.227 -0.591 0.596 0.224
x3 0.421 -0.178 -0.301 0.135 -0.338 0.190 -0.729
x4 0.400 -0.269 -0.450 0.216 -0.311 0.643
x5 0.426 0.272 -0.183 -0.831 -0.118
x6 0.377 0.360 0.479 -0.283 -0.439 0.433 0.196
x7 0.858 -0.486 0.102
说明:a、前两个主成分累计贡献率为91.036%,所有可以用前两个主成分来降维。
b、主成分的表达式:
Y1=0.407x1+0.410x2+0.421x3+0.400x4+0.426x5+0.377x6
Y2=-0.155x2-0.178x3-0.269x4+0.360x6+0.858x7
主成分的经济意义各线性组合中系数较大的几个指标的综合意义确定,成分Y1在x1,x2,x3,x4,x5这这个指标系数较大,在x6,x7系数较小,所有Y1主要反映的是水泥企业的整体规模和收入水平。主成分Y2在x6,x7上面系数较大,在其他指标上面系数较小,因此主成分2主要反映的是水泥企业的盈利能力。
2、计算主成分得分
主成分得分就是把各样本数据代入两个主成分的线下表达式,从而计算主成分得分。
df.pr$scores
df1<-data.frame(df$areas,df.pr$scores)
df1
df1<-data.frame(df$areas,df.pr$scores) > df1 df.areas Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 1 北京 -3.515640 -1.82793290 1.2312186 -0.42043074 -0.20977172 0.058936541 -0.02181273 2 天津 -3.003073 -0.27388041 0.3057919 -0.26320901 0.07346600 0.064959941 -0.08878631 3 河北 3.492990 -1.76504930 -1.1354352 0.83091321 -0.27063999 -0.224951646 -0.06432118 4 山西 -1.366870 -1.86572957 0.2729763 0.44984962 0.17070907 0.104080572 0.11184461 5 内蒙古 -0.502928 -0.61534857 -0.1095937 0.19265129 0.09068896 -0.045207363 0.04420153 6 辽宁 0.179882 -0.10846130 0.1796696 0.21988421 0.17106575 -0.106211797 -0.03572307 7 吉林 1.642415 -1.10452228 -0.8629399 -1.39822126 -0.01338830 -0.426576464 0.02692693 8 黑龙江 -0.781065 -0.10578258 -0.3740632 0.00035975 0.15311967 0.125397343 0.13894098 9 上海 -3.320677 -0.18636325 0.4490147 -0.28078672 0.01768420 -0.026870111 -0.00445479 10 江苏 3.615331 0.32645483 0.4863494 -0.08531633 0.13592028 -0.091041741 0.23298086 11 浙江 1.788433 0.29379000 0.1195645 -0.19348952 0.40015949 0.170807670 -0.08634148 12 安徽 2.083389 1.31107200 0.2515930 -0.38424689 -0.41459944 0.278439752 -0.01419167 13 福建 -1.077652 -0.46565494 0.4875302 0.16515444 0.14027990 -0.316436643 -0.07381221 14 江西 0.527362 1.29710347 0.3464652 -0.17054810 -0.22114898 0.076110671 0.01699948 15 山东 4.770580 0.61728673 1.0270857 -0.34787078 0.21396830 -0.065610349 -0.09328715 16 河南 4.049670 -0.07207734 -0.1732655 -0.52129861 0.38658167 0.203415790 0.04829138 17 湖北 1.862018 0.31272534 0.1341054 -0.21897171 -0.59398630 -0.258499835 -0.02868519 18 湖南 0.503000 0.48817164 0.9677778 0.94672161 0.11604429 -0.224571843 -0.08705109 19 广东 1.818569 0.16884189 0.1008128 0.24875567 0.11485019 0.069973843 -0.00926963 20 广西 0.338820 1.85055716 0.2862296 0.09014668 -0.22736954 0.255088948 -0.04460838 21 海南 -2.750894 0.22608263 0.0454661 -0.39954238 -0.00993694 -0.059410368 -0.03427266 22 重庆 -0.628661 -0.88772794 -0.5940808 -0.10450225 -0.06405085 0.092947440 0.09545077 23 四川 2.181136 -0.24175065 -0.4090686 0.41866229 -0.24938816 0.090796994 -0.09391571 24 贵州 -0.304797 1.08921175 -0.3175461 0.51661253 -0.16962058 0.166790217 0.15655822 25 云南 -0.170936 -0.74929228 -0.1002991 0.56045970 0.14910267 0.006228440 0.04195803 26 西藏 -3.091577 3.26751381 -1.3939541 0.05508742 0.30015544 -0.222173606 -0.06625040 27 陕西 -0.908212 -0.19240249 0.2268532 0.36462016 -0.04504990 -0.175866164 0.02455321 28 甘肃 -1.793673 0.82109182 -0.2513493 0.10918441 -0.01922901 0.037035723 0.00660759 29 青海 -2.623050 0.00150422 -0.2510706 -0.09292648 -0.21900016 0.001762138 0.10736844 30 宁夏 -2.882470 0.31321061 0.0222172 -0.14500038 0.04669932 0.000181659 -0.01947260 31 新疆 -0.131422 -1.92264209 -0.9680548 -0.14270184 0.04668469 0.440474245 -0.18642580
从而得到各个主成分在每个样本点的得分。
3、绘制主成分得分的样本散点图
attach(df1)
plot(df1$Comp.2~df1$Comp.1)
text(df1$Comp.1,df1$Comp.2+0.02,df1$df.areas,pos=3)
运行得到:
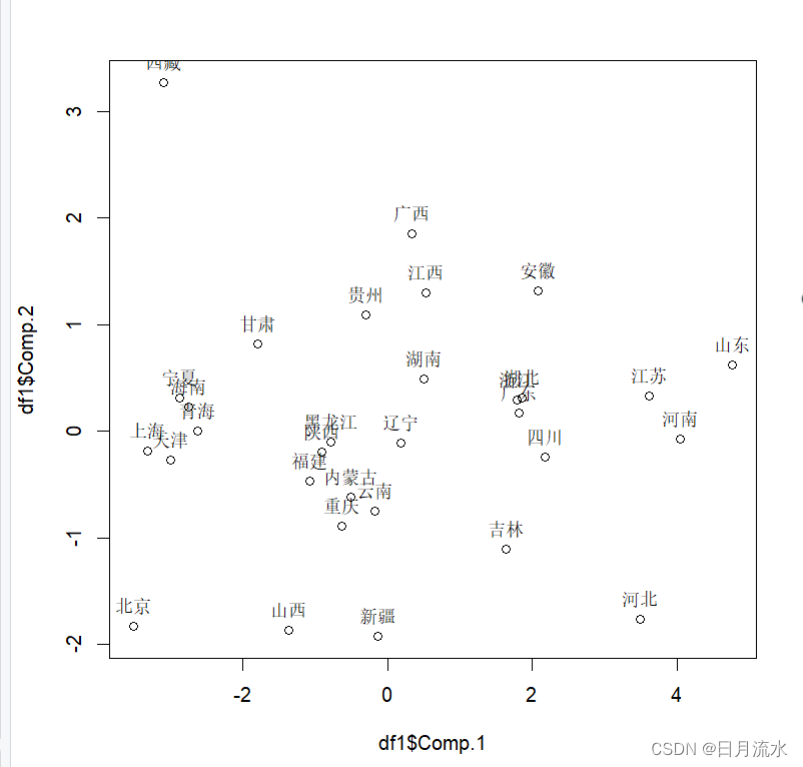
因为主成分只有两个,将样本主成分得分绘制出来,就可以得到样本的分布情况,从而可以对样本进行分类。
四、对样本数据进行因子分析
1、提取因子
在这里使用函数factanal()
fa<-factanal(df[,c('x1','x2','x3','x4','x5','x6','x7')],factors=2,rotation = 'varimax',scores = 'regression')
fa
在这里使用最大方差旋转方法
运行得到:
fa<-factanal(df[,c('x1','x2','x3','x4','x5','x6','x7')],factors=2,rotation = 'varimax',scores = 'regression')
> fa
Call:
factanal(x = df[, c("x1", "x2", "x3", "x4", "x5", "x6", "x7")], factors = 2, scores = "regression", rotation = "varimax")
Uniquenesses:
x1 x2 x3 x4 x5 x6 x7
0.170 0.133 0.009 0.007 0.059 0.005 0.677
Loadings:
Factor1 Factor2
x1 0.824 0.388
x2 0.915 0.176
x3 0.992
x4 0.994
x5 0.845 0.477
x6 0.635 0.770
x7 0.568
Factor1 Factor2
SS loadings 4.605 1.335
Proportion Var 0.658 0.191
Cumulative Var 0.658 0.849
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 15.17 on 8 degrees of freedom.
The p-value is 0.0559
前两个因子累计方差贡献率为84.9%,提取两个因子是合适的,跟进运行得到的因子载荷矩阵可以得到因子f1和f2与原始变量的关系:
x1=0.824f1+0.388f2
x2=0.915f1+0.176f2
x3=0.922f1
x4=0.944f1
x5=0.845f1+0.477f2
x6=0.635f1+0.770f2
x7=0.568f2
如果使用斜交旋转Promax的方法,将得到:
fa<-factanal(df[,c('x1','x2','x3','x4','x5','x6','x7')],factors=2,rotation = 'promax',scores = 'regression')
> fa
Call:
factanal(x = df[, c("x1", "x2", "x3", "x4", "x5", "x6", "x7")], factors = 2, scores = "regression", rotation = "promax")
Uniquenesses:
x1 x2 x3 x4 x5 x6 x7
0.170 0.133 0.009 0.007 0.059 0.005 0.677
Loadings:
Factor1 Factor2
x1 0.685 0.353
x2 0.878 0.101
x3 1.001
x4 1.072 -0.181
x5 0.665 0.452
x6 0.309 0.809
x7 -0.286 0.650
Factor1 Factor2
SS loadings 4.011 1.450
Proportion Var 0.573 0.207
Cumulative Var 0.573 0.780
Factor Correlations:
Factor1 Factor2
Factor1 1.000 -0.489
Factor2 -0.489 1.000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 15.17 on 8 degrees of freedom.
The p-value is 0.0559
斜交旋转的情况下,因子表达式为:
x1=0.568f1+0.353f2
x2=0.878f1+0.101f2
x3=1.001f1
x4=1.072f1-0.181f2
x5=0.665f1+0.452 f2
x6=0.309f1+0.809 f2
x7=-0.286f2+ 0.650f2
斜交旋转的情况下,更能说明因子的因子具体经济含有,从斜交旋转的载荷矩阵可以看到,变量x2,x3,x4在在第一个公共因子的载荷较大,因此,第一个公共因子主要反映企业的规模,变量x6,x7在第二个公共因子的载荷较大,说明第二个公共因子反映企业的盈利能力。
2、计算因子得分
fa$scores
df2<-data.frame(df$areas,fa$scores)
df2
df2 df.areas Factor1 Factor2 1 北京 -1.4143765 -0.1508311 2 天津 -1.3043410 -0.0889328 3 河北 3.5399545 -2.6706415 4 山西 0.4281325 -1.5294351 5 内蒙古 0.3150193 -0.8072694 6 辽宁 0.0608492 -0.1041206 7 吉林 1.4151234 -0.9917456 8 黑龙江 0.0320639 -0.5454919 9 上海 -1.5548788 0.0749349 10 江苏 0.6880203 1.2042261 11 浙江 0.1966863 0.6611251 12 安徽 -0.3187238 2.0231134 13 福建 -0.4136153 -0.2779676 14 江西 -0.8398720 1.6310805 15 山东 0.3714166 2.2721740 16 河南 1.3016494 0.5713237 17 湖北 0.4532688 0.7642714 18 湖南 -0.4557515 0.7670075 19 广东 0.5397438 0.3251183 20 广西 -1.0926484 1.9075718 21 海南 -1.2837594 0.0763441 22 重庆 0.6843438 -1.2564094 23 四川 1.4231037 -0.4835207 24 贵州 -0.2352031 0.2985555 25 云南 0.6242982 -1.0586728 26 西藏 -1.7056631 0.3287434 27 陕西 -0.2081481 -0.3079663 28 甘肃 -0.8373975 0.0894333 29 青海 -0.7299168 -0.4712487 30 宁夏 -1.2786471 -0.0284181 31 新疆 1.5992689 -2.2223515
3、跟据计算得出的因子得分,把样本点绘制的散点图上