Diffusion Models专栏文章汇总:入门与实战
前言:有不少订阅我专栏的读者问diffusion models很深奥读不懂,需要先看一些什么知识打下基础?虽然diffusion models是一个非常前沿的工作,但肯定不是凭空产生的,背后涉及到非常多深度学习的知识,我将从配分函数、基于能量模型、马尔科夫链蒙特卡洛采样、得分匹配、比率匹配、降噪得分匹配、桥式采样、深度玻尔兹曼机、对比散度、随机最大似然、伪似然等方面,总结一些经典的知识点,供读者参考。
系列文章目录:
1、Diffusion Models/Score-based Generative Models背后的深度学习原理(1):配分函数
2、Diffusion Models/Score-based Generative Models背后的深度学习原理(2):基于能量模型和受限玻尔兹曼机
3、Diffusion Models/Score-based Generative Models背后的深度学习原理(3):蒙特卡洛采样法和重要采样法
4、Diffusion Models/Score-based Generative Models背后的深度学习原理(4):随机最大似然和对比散度
5、Diffusion Models/Score-based Generative Models背后的深度学习原理(5):伪似然和蒙特卡洛近似配分函数
6、Diffusion Models/Score-based Generative Models背后的深度学习原理(6):噪声对比估计
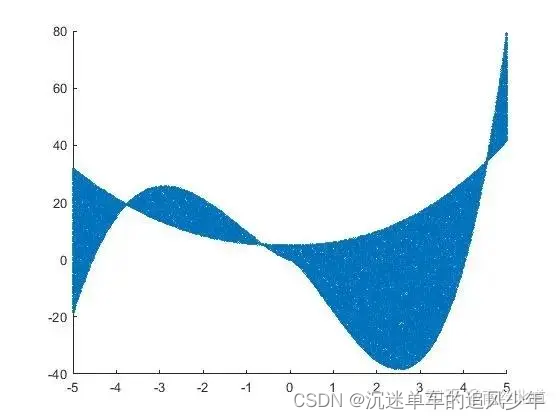
蒙特卡罗近似配分函数及其梯度需要直接处理配分函数。有些其他方法通过训 练不需要计算配分函数的模型来绕开这个问题。这些方法大多数都基于以下观察: 无向概率模型中很容易计算概率的比率。这是因为配分函数同时出现在比率的分子 和分母中,互相抵消:
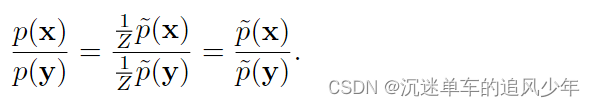
伪似然正是基于条件概率可以采用这种基于比率的形式,因此可以在没有配分 函数的情况下进行计算。假设我们将 x 分为 a,b 和 c,其中 a 包含我们想要的条件分布的变量,b 包含我们想要条件化的变量,c 包含除此之外的变量:
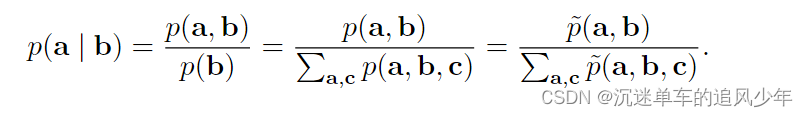
以上计算需要边缘化 a,假设 a 和 c 包含的变量并不多,那么这将是非常高效的操 作。在极端情况下,a 可以是单个变量,c 可以为空,那么该计算仅需要估计与单 个随机变量值一样多的 。
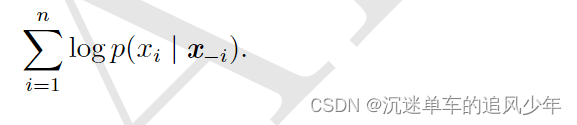
不幸的是,为了计算对数似然,我们需要边缘化很多变量。如果总共有 n 个变 量,那么我们必须边缘化 n 1 个变量。根据概率的链式法则,我们有:
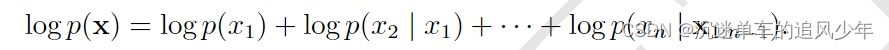
在这种情况下,我们已经使 a 尽可能小,但是 c 可以大到 x2:n。如果我们简单地将 c 移 到 b 中以减少计算代价,那么会发生什么呢?这便产生了 伪似然(pseudolikelihood)(Besag, 1975)目标函数,给定所有其他特征 ,预测特征
的值:
如果每个随机变量有 k 个不同的值,那么计算 需要
次估计,而计算配 分函数需要
次估计。
这看起来似乎是一个没有道理的策略,但可以证明最大化伪似然的估计是渐近 一致的 (Mase, 1995)。当然,在数据集不趋近于大采样极限的情况下,伪似然可能表 现出与最大似然估计不同的结果。
基于伪似然的方法的性能在很大程度上取决于模型是如何使用的。对于完全联 合分布 p(x) 模型的任务(例如密度估计和采样),伪似然通常效果不好。对于在训练期间只需要使用条件分布的任务而言,它的效果比最大似然更好,例如填充少量 的缺失值。如果数据具有规则结构,使得 S 索引集可以被设计为表现最重要的相关 性质,同时略去相关性可忽略的变量,那么广义伪似然策略将会非常有效。例如,在 自然图像中,空间中相隔很远的像素也具有弱相关性,因此广义伪似然可以应用于 每个 S 集是小的局部空间窗口的情况。
伪似然估计的一个弱点是它不能与仅在 ~p(x) 上提供下界的其他近似一起使用, 例如第十九章中介绍的变分推断。这是因为 ~p 出现在了分母中。分母的下界仅提供 了整个表达式的上界,然而最大化上界没有什么意义。这使得我们难以将伪似然方 法应用于诸如深度玻尔兹曼机的深度模型,因为变分方法是近似边缘化互相作用的 多层隐藏变量的主要方法之一。尽管如此,伪似然仍然可以用在深度学习中,它可 以用于单层模型,或使用不基于下界的近似推断方法的深度模型中。
伪似然比 SML 在每个梯度步骤中的计算代价要大得多,这是由于其对所有条 件进行显式计算。但是,如果每个样本只计算一个随机选择的条件,那么广义伪 似然和类似标准仍然可以很好地运行,从而使计算代价降低到和 SML 差不多的程 度 (Goodfellow et al., 2013d)。
虽然伪似然估计没有显式地最小化 log Z,但是我们仍然认为它具有类似负相的 效果。每个条件分布的分母会使得学习算法降低所有仅具有一个变量不同于训练样本的状态的概率。