【力扣hot100】刷题笔记Day18

news2024/11/17 9:59:59

前言

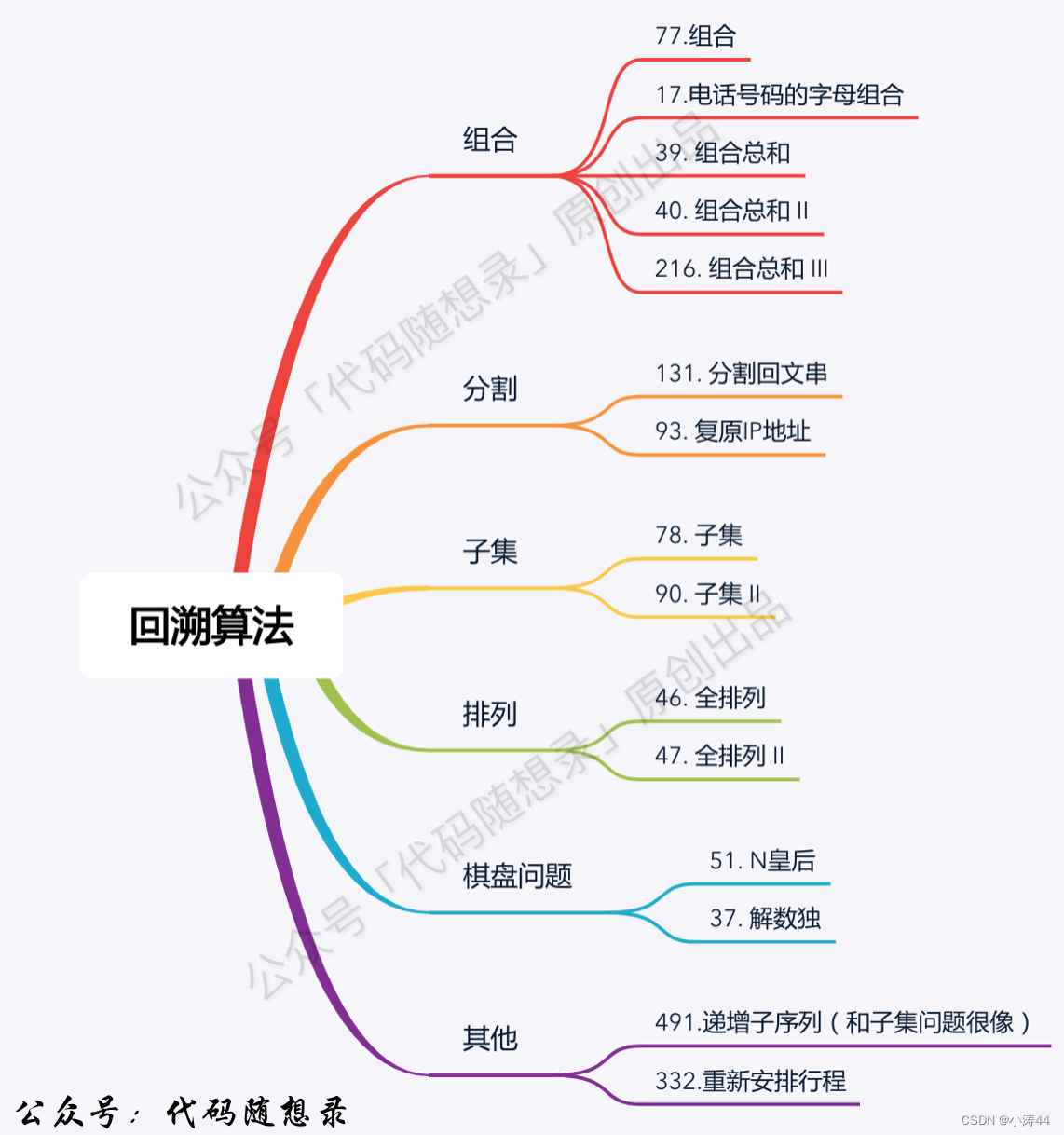
晚上巩固一下今天的回溯题，基础不牢地动山摇，po一张代码随想录总结的

组合补充

77. 组合 - 力扣（LeetCode）

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        path = []
        res = []
        def backtrack(start = 1):
            if len(path) == k:
                res.append(path[:])
                return
            # for i in range(start, n + 1): # [start,n]
            for i in range(start, n + 2 - (k - len(path))): # 剪枝，个数不够的不需要遍历了
                path.append(i)
                backtrack(i+1)
                path.pop()
        backtrack()
        return res

40. 组合总和 II - 力扣（LeetCode）

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        n = len(candidates)
        path = []
        res = []
        def backtrack(start, target):
            if target == 0:
                res.append(path[:])
                return
            for i in range(start, n):
                if target - candidates[i] < 0:
                    return  # 树枝剪枝
                if i > start and candidates[i] == candidates[i-1]:
                    continue  # 树层去重
                path.append(candidates[i])
                backtrack(i+1, target - candidates[i])
                path.pop()
        backtrack(0, target)
        return res

216. 组合总和 III - 力扣（LeetCode）

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        path = []
        res = []
        def backtrack(start, n):
            if len(path) == k:
                if n == 0:
                    res.append(path[:])
                return  # 剪枝，个数到了
            for i in range(start, 10):
                if n - i < 0: return  # 剪枝，总和小了
                path.append(i)
                backtrack(i+1, n-i)
                path.pop()
        backtrack(1, n)
        return res

子集补充

90. 子集 II - 力扣（LeetCode）

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        if n == 0: return []
        nums.sort()  # 排序
        res = []
        path = []
        # used = [0] * n
        def backtrack(start = 0):
            res.append(path[:])
            for i in range(start, n):
                # if i != 0  and nums[i] == nums[i-1] and used[i-1] == 0:
                if i > start and nums[i] == nums[i-1]:
                    continue  # 树层去重
                # used[i] = 1
                path.append(nums[i])
                backtrack(i+1)
                # used[i] = 0
                path.pop()
        backtrack()
        return res

全排列补充

47. 全排列 II - 力扣（LeetCode）

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        path = []
        res = []
        nums.sort()
        n = len(nums)
        used = [0] * n
        def backtrack():
            if len(path) == n:
                res.append(path[:])
                return
            for i in range(n):
                if i != 0 and nums[i] == nums[i-1] and used[i-1] == 0:
                    continue  # 树层去重，注意不是return
                if used[i] == 0:
                    used[i] = 1
                    path.append(nums[i])
                    backtrack()
                    used[i] = 0
                    path.pop()
        backtrack()
        return res