题目名称:走楼梯
时间限制:1000ms内存限制:256M
题目描述
现在有一截楼梯,根据你的腿长,你一次能走 1 级或 2 级楼梯,已知你要走 n 级楼梯才能走到你的目的楼层,请实现一个方法,计算你走到目的楼层的方案数。(测试用例仅做参考,我们会根据代码质量进行评分)
输入描述:
输入整数n。(1<=n<=50)
输出描述:
输出方案数。
示例
示例1
输入5
输出8
提示
思路说明:
你一次能走 1 级或 2 级楼梯,已知你要走 n 级楼梯才能走到你的目的楼层,则设F(n)为走到n阶的种数,则F(n)=F(n-1)+F(n-2)。
当n=1时,F(1)=1,n=2时,F(2)=2, F(3)=4,…符合斐波那契数列的特征。
斐波那契数列(百度百科)
“斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
基础实现代码:
def f (n):
if n <= 2:
return n
return f (n - 1) + f (n - 2)
if __name__ == "__main__":
n = int(input().strip())
ways = f(n)
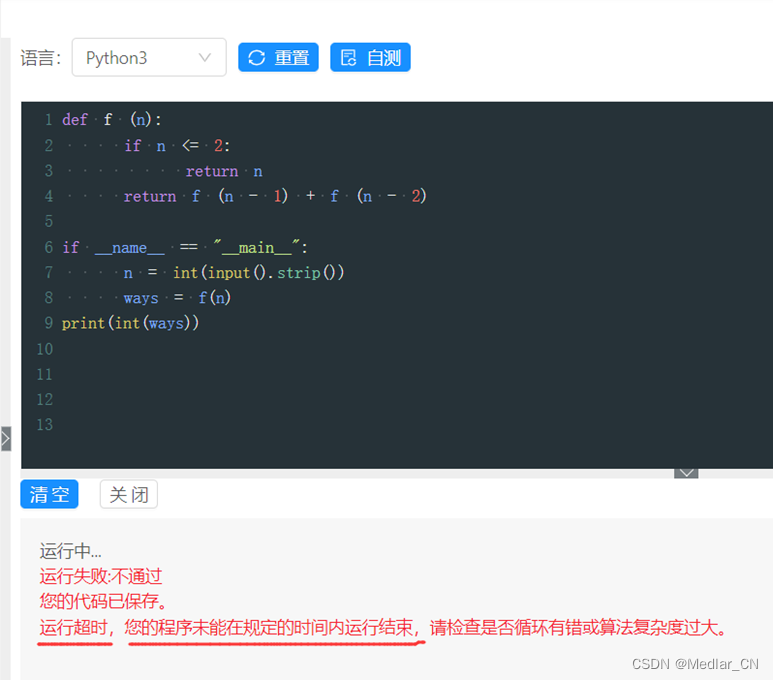
print(int(ways))问题:
但该方法不能通过系统测试,未能在规定时间内运行结束。。
算法需优化。
改进:动态计算
引自:Python学习教程:算法如何解决楼梯台阶问题_千锋python和唐唐的博客-CSDN博客_python中关于台阶的走法
在函数体内实现了迭代,每个循环只计算第n – 1和n-2,不是整个函数去迭代,且只计算n-1次,不重复计算。
代码:
def fibonacci(n):
a, b = 1, 2
#每次只计算第n – 1和n-2,不是整个函数去迭代,且只计算n-1次,不重复计算。
for _ in range(n - 1):
a, b = b, a + b
return a
if __name__ == "__main__":
n = int(input().strip())
ways = fibonacci(n)
print(int(ways))思路2:排列组合方法
引自:爬楼梯算法的数学思路_shangjun2018的博客-CSDN博客_爬台阶算法
走了n-1个1和一个2时,它的方法总数其实应该是:
sum = 1 + Cnk(n-1, 1) + Cnk(n-2, 2) + … Cnk(n/2 , n/2) 偶数情况。
sum = 1 + Cnk(n-1, 1) + Cnk(n-2, 2) + … Cnk(n//2 + 1 , n//2 - 1) 奇数情况。
注: n//2 为: 用n整除2, 然后取得的数向下取整。 (2.1取2, 2.9取2)
实现代码:
def computer(n):
all_ways = 1
if n % 2 == 0:
stop_num = int(n / 2)
for i in range(1, stop_num + 1):
all_ways += Cnk(n - i, i)
if n % 2 == 1:
stop_num = (n // 2) + 1
for i in range(1, stop_num + 1):
all_ways += Cnk(n - i, i)
return all_ways
def Cnk(n, k):
value1 = 1
for i in range(k):
value1 = value1 * (n - i)
value2 = 1
for i in range(1, k + 1):
value2 = value2 * i
ans = value1 / value2
return ans
if __name__ == "__main__":
n = int(input().strip())
ways = computer(n)
print(int(ways))扩展:步数:{集合X}
原文链接:https://blog.csdn.net/chen801090/article/details/100984687
从集合X中取步数的要求下爬楼梯。例如X = {1,3,5},那么我们的算法应该是f(n) = f(n – 1) + f(n – 3) + f(n – 5)。如果n <0,那么我们应该返回0,因为我们不能爬负数。
def staircase(n, X):
if n < 0:
return 0
elif n == 0:
return 1
elif n in X:
return 1 + sum(staircase(n - x, X) for x in X if x < n)
else:
return sum(staircase(n - x, X) for x in X if x < n)这也很慢(O(|X|^N)),因为也重复计算了。
我们可以使用动态编程来加快速度。
每次的输入cache[i]将包含我们可以用集合X到达台阶i的方法的数量。然后,我们将使用与之前相同的递归从零开始构建数组:
def staircase(n, X):
cache = [0 for _ in range(n + 1)]
cache[0] = 1
for i in range(n + 1):
cache[i] += sum(cache[i - x] for x in X if i - x > 0)
cache[i] += 1 if i in X else 0
return cache[-1]现在时间复杂度为O(N * |X|),空间复杂度为O(N)。