视频地址 :
回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili
基本概念
1 . 例子
例如从abc和def(n = 2)中各选出一个组成新的字符串?

如果n很大 , 这个时候for循环的表达能力有限 ;
2 . 原问题 和 子问题

3 . 增量构造答案
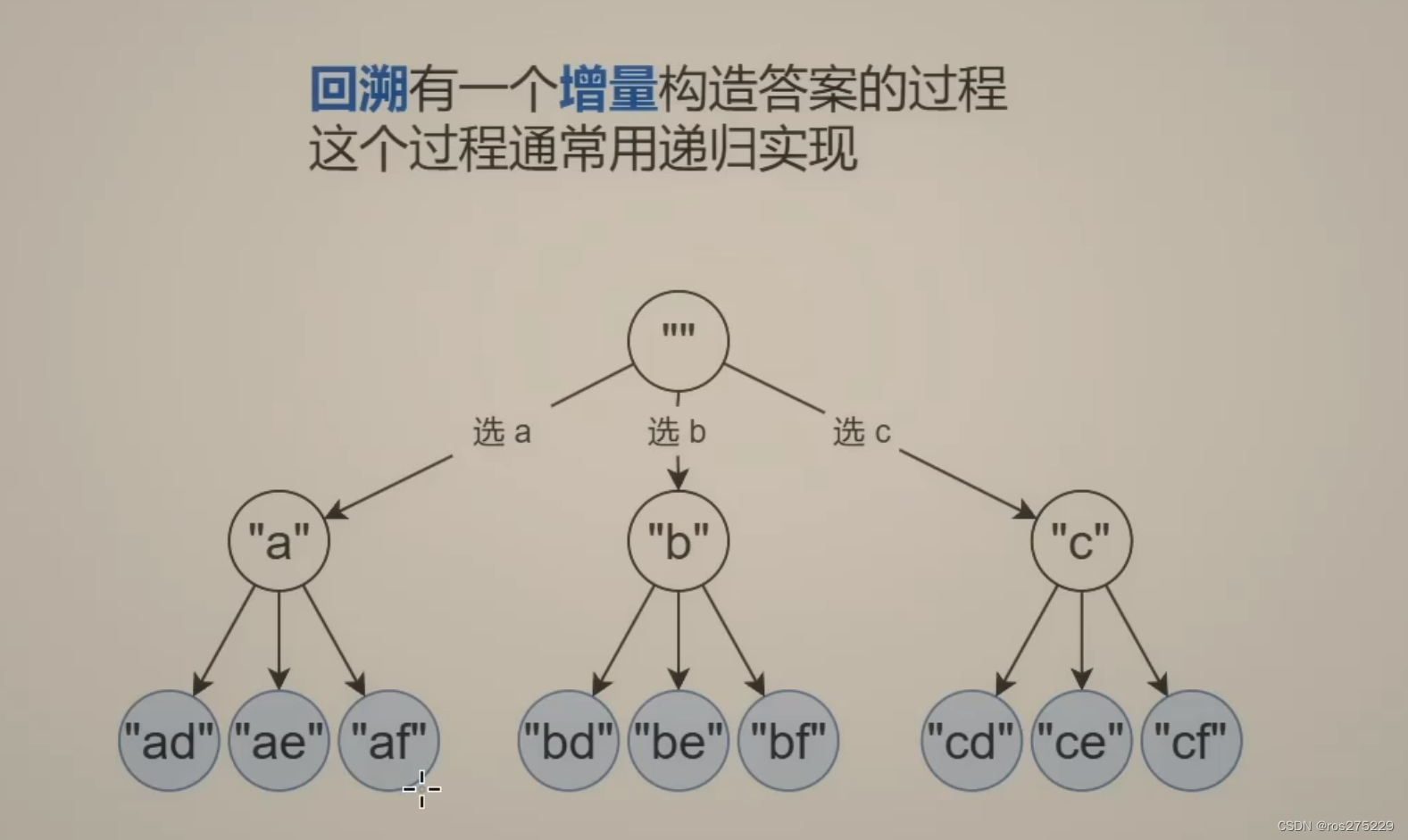
这个增量构造答案的过程就是回溯的特点 ;
回溯三问

关于恢复现场的理解
在递归到某一“叶子节点”(非最后一个叶子)时,答案需要向上返回,而此时还有其他的子树(与前述节点不在同一子树)未被递归到,又由于path为全局变量。若直接返回,会将本不属于该子树的答案带上去,故需要恢复现场。
恢复现场的方式为:在递归完成后 dfs(i+1); 后,进行与“当前操作”相反的操作,“反当前操作”。
17 . 电话号码的字母组合
这也就是n(n=8)个字符串中选两个的组合问题 ;
思路 :
1 . 先创建一个下标 与 对应字符串映射的数组,这里使用hash表进行映射也是可以的 ;
2 . 对于回溯 , 如果到了叶子节点 , 那么就直接添加即可 , 对于每一个path[i],都是存放digits[i]中数字字符对应字符串中的一个字符 , 遍历该字符串 , 对每一个字符进行递归操作 ;
3 . 对于不用恢复现场 : 因为每次递归到 i,一定会修改 path【i】,那么递归到终点时,每个 path【i】 都被覆盖成要枚举的字母,所以不需要恢复现场。
代码实现 :
class Solution {
public:
const string mp[10] = {
"", //0
"", //1
"abc", //2
"def", //3
"ghi", //4
"jkl", //5
"mno", //6
"pqrs", //7
"tuv", //8
"wxyz", //9
};
vector<char> path ;
vector<string> ans ;
int n ;
string get(){
string tmp = "" ;
for(char c : path){
tmp += c ;
}
return tmp ;
}
void dfs(string digits , int i){
// 先写递归终止条件
if(i == n){
ans.push_back(get()) ;
return ; // 回溯
}
for(char c : mp[digits[i]-'0']){
path[i] = c ;
dfs(digits , i + 1) ;
// 因为每一次path[i]都会被覆盖 , 那么就不用进行回溯
}
}
vector<string> letterCombinations(string digits) {
n = digits.size() ;
if(n == 0) return ans ;
path.resize(n) ;
dfs(digits , 0) ;
return ans ;
}
};更加优雅的写法 :
class Solution {
string MAPPING[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public:
vector<string> letterCombinations(string digits) {
int n = digits.length();
if (n == 0) return {};
vector<string> ans;
string path(n, 0); // 本题 path 长度固定为 n
function<void(int)> dfs = [&](int i) {
if (i == n) {
ans.emplace_back(path);
return;
}
for (char c : MAPPING[digits[i] - '0']) {
path[i] = c; // 直接覆盖
dfs(i + 1);
}
};
dfs(0);
return ans;
}
};
78 . 子集
链接 :
. - 力扣(LeetCode)
法一(对于每一个数选或不选) :

class Solution {
public:
vector<vector<int>> ans ;
vector<int> path ;
void dfs(vector<int>& nums , int i){
if(i==nums.size()){
ans.push_back(path) ;
return ;// 回溯
}
// 不选
dfs(nums,i+1) ;// 不选i
// 选
path.push_back(nums[i]) ;
dfs(nums,i+1) ;
path.pop_back() ;
}
vector<vector<int>> subsets(vector<int>& nums) {
if(nums.size()==0) return ans ;
ans.clear() ;
path.clear() ;
dfs(nums,0) ;
return ans ;
}
};法二(枚举第i个数选谁):
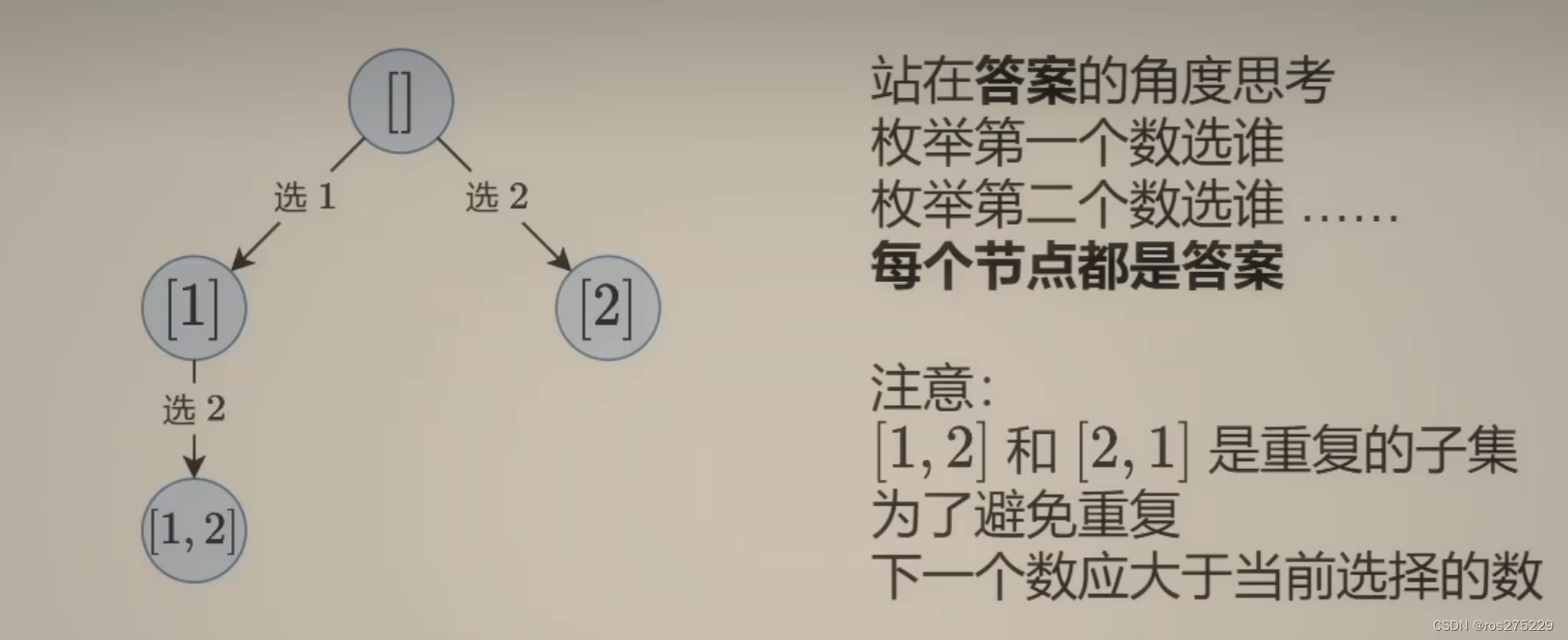
这样的话 每一个结点都是答案 ;


class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
void backtrack(vector<int>& nums,int idx){
ans.push_back(path);
if(idx >= nums.size()) return;
for(int i=idx;i<nums.size();i++){
path.push_back(nums[i]);
backtrack(nums,i+1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
path.clear();
ans.clear();
backtrack(nums,0);
return ans;
}
};131 . 分割回文串
链接 :
. - 力扣(LeetCode)
思路 :

代码 (枚举子串结束位置):
class Solution {
public:
bool pd(string s , int l ,int r){
while(l <= r){
if(s[l++] != s[r--])
return false;
}
return true ;
}
vector<vector<string>> ans ;
vector<string> path ;
int n = 0 ;
// 答案视角 , 判断每一个子串结束的地方
void dfs(string s , int i){
if(i==n){
ans.push_back(path) ;
return ;
}
for(int j=i;j<n;j++){ // 枚举子串结束的位置
if(pd(s,i,j)){
path.push_back(s.substr(i,j-i+1)) ;
dfs(s,j+1) ;
path.pop_back();// 恢复现场
}
}
}
vector<vector<string>> partition(string s) {
n = s.size() ;
dfs(s,0) ;
return ans ;
}
};代码(每个分割点选不选) :
class Solution {
public:
bool pd(string s , int l ,int r){
while(l <= r){
if(s[l++] != s[r--])
return false;
}
return true ;
}
vector<vector<string>> partition(string s) {
vector<vector<string>> ans ;
vector<string> path ;
// 判断每个逗号选或不选
int n = s.size() ;
// start 表示这一段回文串的开始位置
function<void(int,int)> dfs = [&](int i,int start){
if(i==n){
ans.push_back(path) ;
return ;
}
// 不选i-i+1
if(i < n - 1){
dfs(i+ 1, start) ;
}
// 选
if(pd(s,start,i)){
path.push_back(s.substr(start,i-start+1));
dfs(i + 1 , i + 1 ) ;
path.pop_back() ;
}
};
dfs(0 , 0) ;
return ans ;
}
};