RRT算法学习及MATLAB演示

文章目录

1 前言
2 算法简介
3 MATLAB实现
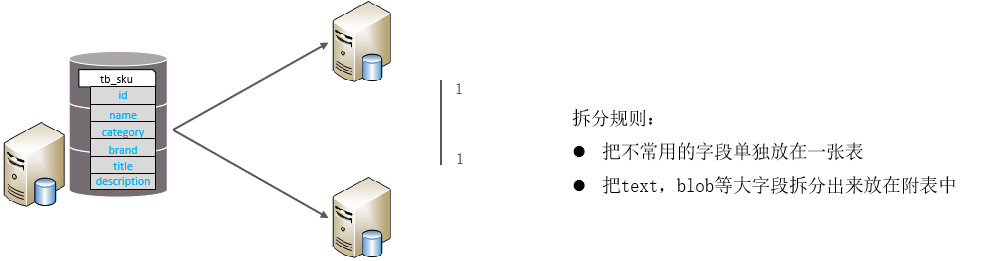
- 3.1 定义地图
- 3.2 绘制地图
- 3.3 定义参数
- 3.4 绘制起点和终点
- 3.5 RRT算法
- - 3.5.1 代码
  - 3.5.2 效果
  - 3.5.3 代码解读
4 参考
5 完整代码

1 前言

RRT（Rapid Random Tree）算法，即快速随机树算法，是LaValle在1998年首次提出的一种高效的路径规划算法。RRT算法以初始的一个根节点，通过随机采样的方法在空间搜索，然后添加一个又一个的叶节点来不断扩展随机树。当目标点进入随机树里面后，随机树扩展立即停止，此时能找到一条从起始点到目标点的路径。

两个代码文件见最后一节。

2 算法简介

效果预览图
在这里插入图片描述
算法的计算过程如下：
step1：初始化随机树。将环境中起点作为随机树搜索的起点，此时树中只包含一个节点即根节点；
stpe2：在环境中随机采样。在环境中随机产生一个点，若该点不在障碍物范围内则计算随机树中所有节点到的欧式距离，并找到距离最近的节点，若在障碍物范围内则重新生成并重复该过程直至找到;
stpe3：生成新节点。在和连线方向，由指向固定生长距离生成一个新的节点，并判断该节点是否在障碍物范围内，若不在障碍物范围内则将添加到随机树中，否则的话返回step2重新对环境进行随机采样；
step4：停止搜索。当和目标点之间的距离小于设定的阈值时，则代表随机树已经到达了目标点，将作为最后一个路径节点加入到随机树中，算法结束并得到所规划的路径。

3 MATLAB实现

3.1 定义地图

地图是模拟的栅格地图，resolution表示每个格子的长度，这里设置为1，地图范围为 $x\in[-15,15]$ , $y\in[-15,15]$ 。障碍物的形状为矩形，定义方式为矩形的左下角坐标及其水平长度和竖直长度。wall_obstacle位于地图边界，block_obstacle位于地图内部。

%% Define the map
resolution = 1; % resolution, cell length

% Map boundaries
left_bound = -15;
right_bound = 15;
lower_bound = -15;
upper_bound = 15;

% Wall obstacle [left_down_x,left_down_y,horizontal_length,vertical_length]
wall_obstacle(1,:) = [   left_bound,   lower_bound,                        1, upper_bound-lower_bound-1]; % left boundary
wall_obstacle(2,:) = [ left_bound+1,   lower_bound, right_bound-left_bound-1,                         1]; % bottom boundary
wall_obstacle(3,:) = [right_bound-1, lower_bound+1,                        1, upper_bound-lower_bound-1]; % right boundary
wall_obstacle(4,:) = [   left_bound, upper_bound-1, right_bound-left_bound-1,                         1]; % up boundary

% Blcok obstacle [left_down_x,left_down_y,horizontal_length,vertical_length]
block_obstacle(1,:) = [0,-10,10,5]; % block obstacle 1
block_obstacle(2,:) = [-5,5,5,9]; % block obstacle 2
block_obstacle(3,:) = [-5,-2,5,4]; % block obstacle 3

ob = [block_obstacle; wall_obstacle];

3.2 绘制地图

%% Draw the map
figure(1); % create a figure

% Figure setting
set(gca,'XLim',[left_bound right_bound]); % x axis range
set(gca,'XTick',[left_bound:resolution:right_bound]); % x axis tick
set(gca,'YLim',[lower_bound upper_bound]); % y axis range
set(gca,'YTick',[lower_bound:resolution:upper_bound]); % y axis tick
grid on
axis equal
title('RRT');
xlabel('x');
ylabel('y');

hold on

% Draw the obstacles
for i=1:1:size(ob,1)
    fill([ob(i,1),ob(i,1)+ob(i,3),ob(i,1)+ob(i,3),ob(i,1)],...
         [ob(i,2),ob(i,2),ob(i,2)+ob(i,4),ob(i,2)+ob(i,4)],'k');
end

结果如下图所示，这里用红框标出了wall_obstacle，用绿色数字表示block_obstacle。
在这里插入图片描述

3.3 定义参数

grow_distance指新生长出的节点与其父节点的距离，这里设为1；goal_distance指的是如果新生长出的节点落在这个范围里，则认为已经到达终点；goal的位置设为 $[- 10, - 10]$ ，start的位置设为 $[13, 10]$ 。

%% Initialize parameters
grow_distance = 1; % distance between parent node and the derived child node
goal_radius = 1.5; % can be considered as reaching the goal once within this range
% Goal point position
goal.x = -10;
goal.y = -10;
% Start point position
start.x = 13;
start.y = 10;

3.4 绘制起点和终点

%% Draw the start point and the end point
h_start = plot(start.x,start.y,'b^','MarkerFaceColor','b','MarkerSize',5*resolution);
h_goal = plot(goal.x,goal.y,'m^','MarkerFaceColor','m','MarkerSize',5*resolution);

% Draw the goal circle
theta = linspace(0,2*pi);
goal_circle.x = goal_radius*cos(theta) + goal.x;
goal_circle.y = goal_radius*sin(theta) + goal.y;
plot(goal_circle.x,goal_circle.y,'--k','LineWidth',0.8*resolution);

在这里插入图片描述

3.5 RRT算法

这一部分主要是用于演示RRT算法是怎么建树，怎么到达给定终点，侧重于展示RRT的思想，如果用于工程实现，则需要用C++等高级语言重写，并且使用严谨的数据结构。

3.5.1 代码

注意需要另外写一个函数find_closet_node.m

function [angle,min_idx] = find_closet_node(rd_x,rd_y,tree)
    distance = [];
    i = 1;
    while i <= length(tree.child) % should not use size() function
        dx = rd_x - tree.child(i).x;
        dy = rd_y - tree.child(i).y;
        distance(i) = sqrt(dx^2 + dy^2);
        i = i+1;
    end
    [~,min_idx] = min(distance);
    angle = atan2(rd_y-tree.child(min_idx).y, rd_x-tree.child(min_idx).x);
end

下面的代码承接3.4节即可

%% RRT Algorithm
% Initialize the random tree(in the form of struct)
tree.child = []; % current node
tree.parent = []; % current node's parent
tree.distance = []; % current node's distance to the start

tree.child = start;
tree.parent = start;
tree.distance = 0;

new_node.x = start.x;
new_node.y = start.y;

goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);

% Main loop
while goal_distance > goal_radius
    random_point.x = (right_bound - left_bound) * rand() + left_bound; % random x value between x limit
    random_point.y = (upper_bound - lower_bound) * rand() + lower_bound; % random y value between y limit
    handle_1 = plot(random_point.x,random_point.y,'p','MarkerEdgeColor',[0.9290 0.6940 0.1250],'MarkerFaceColor',[0.9290 0.6940 0.1250],'MarkerSize',8*resolution); % draw the randomly generated point
    [angle,min_idx] = find_closet_node(random_point.x,random_point.y,tree);
    
    % pause(0.5)
    handle_2 = plot([tree.child(min_idx).x,random_point.x],[tree.child(min_idx).y,random_point.y],'-','Color',[0.7 0.7 0.7],'LineWidth',0.8*resolution); % draw the segment between the closest tree node and the randomly generated point
    
    % pause(0.5)
    new_node.x = tree.child(min_idx).x + grow_distance*cos(angle);
    new_node.y = tree.child(min_idx).y + grow_distance*sin(angle);
    handle_3 = plot(new_node.x,new_node.y,'.r','MarkerFaceColor','r','MarkerSize',10*resolution); % draw the potential new node
    
    flag = 1; % default: valid node

    % Judge if the new node is inside the obstacle
    step = 0.01;
    if new_node.x < tree.child(min_idx).x
        step = -step;
    end
    for k=1:1:size(ob,1)
        for i=tree.child(min_idx).x:step:new_node.x
            if angle>pi/2-5e-02 && angle<pi/2+5e-02
                j = tree.child(min_idx).y+1;
            elseif angle>-pi/2-5e-02 && angle<-pi/2+5e-02
                j = tree.child(min_idx).y-1;
            else
                j=tree.child(min_idx).y+(i-tree.child(min_idx).x)*tan(angle);
            end
            if i>=ob(k,1) && i<=(ob(k,1)+ob(k,3))
                if j >=ob(k,2) && j<=ob(k,2)+ob(k,4)
                    flag = 0; % invalid node
                    break
                end
            end
        end
        if flag==0
            break
        end
    end

    % pause(0.5)
    if flag==1
        tree.child(end+1) = new_node;
        tree.parent(end+1) = tree.child(min_idx);
        tree.distance(end+1) = 1 + tree.distance(min_idx);
        goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);
        delete(handle_3)
        plot(new_node.x,new_node.y,'.g','MarkerFaceColor','g','MarkerSize',10*resolution); % draw the new node
        % pause(0.2)
        plot([tree.child(min_idx).x,new_node.x],[tree.child(min_idx).y,new_node.y],'-k','LineWidth',0.8*resolution); % draw the segment between the closest tree node and the new node
    end
    
    % pause(0.5)
    delete(handle_1);
    delete(handle_2);
    % pause(0.5)
end

3.5.2 效果

在这里插入图片描述

3.5.3 代码解读

首先是初始化一个tree结构体，含有child, parent, distance三个成员，三者均为列表。child用于存储所有节点，在相同索引位置，parent存储child的父节点，distance存储child到起点的距离（沿着树的距离，不是直线距离）。然后对这三个成员进行初始化。
```
% Initialize the random tree(in the form of struct)
tree.child = []; % current node
tree.parent = []; % current node's parent
tree.distance = []; % current node's distance to the start

tree.child = start;
tree.parent = start;
tree.distance = 0;
```
定义全局变量，new_node，用于存储新衍生出来的节点，用起点对其初始化。
定义全局变量，goal_distance，用于存储new_node到终点的距离。
```
new_node.x = start.x;
new_node.y = start.y;

goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);
```

进入主循环，只要new_node尚未到达终点范围，则循环继续。

每个循环中，在地图范围内生成一个随机点，然后找到距离该随机点最近的树上的节点（借助自定义函数find_closet_node实现），返回该点的索引，以及这两点连线的角度。【生成的随机点用黄色五角星表示】【随机点与最近的树上节点的连线用灰色表示】

random_point.x = (right_bound - left_bound) * rand() + left_bound; % random x value between x limit
random_point.y = (upper_bound - lower_bound) * rand() + lower_bound; % random y value between y limit
handle_1 = plot(random_point.x,random_point.y,'p','MarkerEdgeColor',[0.9290 0.6940 0.1250],'MarkerFaceColor',[0.9290 0.6940 0.1250],'MarkerSize',8*resolution); % draw the randomly generated point
[angle,min_idx] = find_closet_node(random_point.x,random_point.y,tree);

% pause(0.5)
handle_2 = plot([tree.child(min_idx).x,random_point.x],		[tree.child(min_idx).y,random_point.y],'-','Color',[0.7 0.7 0.7],'LineWidth',0.8*resolution); % draw the segment between the closest tree node and the randomly generated point

function [angle,min_idx] = find_closet_node(rd_x,rd_y,tree)
    distance = [];
    i = 1;
    while i <= length(tree.child) % should not use size() function
        dx = rd_x - tree.child(i).x;
        dy = rd_y - tree.child(i).y;
        distance(i) = sqrt(dx^2 + dy^2);
        i = i+1;
    end
    [~,min_idx] = min(distance);
    angle = atan2(rd_y-tree.child(min_idx).y, rd_x-tree.child(min_idx).x);
end

在这两点连线上，生成一个新节点，新节点与树上的节点距离为1，默认该节点是有效的，也即不会与障碍物干涉的。【新节点用红色实心点表示】

	% pause(0.5)
    new_node.x = tree.child(min_idx).x + grow_distance*cos(angle);
    new_node.y = tree.child(min_idx).y + grow_distance*sin(angle);
    handle_3 = plot(new_node.x,new_node.y,'.r','MarkerFaceColor','r','MarkerSize',10*resolution); % draw the potential new node
    
    flag = 1; % default: valid node

然后判断生成的新节点与树上节点的连线上的点是否位于障碍物内，也即判断新节点是否会导致路径与障碍物干涉，如果发生干涉，则把flag设置为0。

% Judge if the new node is inside the obstacle
step = 0.01;
if new_node.x < tree.child(min_idx).x
    step = -step;
end
for k=1:1:size(ob,1)
    for i=tree.child(min_idx).x:step:new_node.x
        if angle>pi/2-5e-02 && angle<pi/2+5e-02
            j = tree.child(min_idx).y+1;
        elseif angle>-pi/2-5e-02 && angle<-pi/2+5e-02
            j = tree.child(min_idx).y-1;
        else
            j=tree.child(min_idx).y+(i-tree.child(min_idx).x)*tan(angle);
        end
        if i>=ob(k,1) && i<=(ob(k,1)+ob(k,3))
            if j >=ob(k,2) && j<=ob(k,2)+ob(k,4)
                flag = 0; % invalid node
                break
            end
        end
    end
    if flag==0
        break
    end
end

如果没有发生干涉，则将该点加入child列表，并将上一个点加入parent列表，该点距离起点的距离等于grow_distance加上上一个点距离起点的距离。【如果新节点在可行区域，则将该节点画为绿色】【该可行新节点与上一个节点的连线为黑色】【擦除之前生成的五角星随机点】【擦除之前五角星随机点与树上节点的连线】

% pause(0.5)
if flag==1
	 tree.child(end+1) = new_node;
	 tree.parent(end+1) = tree.child(min_idx);
	 tree.distance(end+1) = grow_distance + tree.distance(min_idx);
	 goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);
	 delete(handle_3)
	 plot(new_node.x,new_node.y,'.g','MarkerFaceColor','g','MarkerSize',10*resolution); % draw the new node
	 % pause(0.2)
	 plot([tree.child(min_idx).x,new_node.x],[tree.child(min_idx).y,new_node.y],'-k','LineWidth',0.8*resolution); % draw the segment between the closest tree node and the new node
end

% pause(0.5)
delete(handle_1);
delete(handle_2);
% pause(0.5)

4 参考

RRT, RRT* & Random Trees
全局路径规划 - RRT算法原理及实现

5 完整代码

将下面两个文件放在同一文件夹下，运行（或分节运行）RRT_learn.m即可。此外，需要动态观察算法效果则把所有pause语句取消注释。
find_closest_node.m

function [angle,min_idx] = find_closest_node(rd_x,rd_y,tree)
    distance = [];
    i = 1;
    while i <= length(tree.child) % should not use size() function
        dx = rd_x - tree.child(i).x;
        dy = rd_y - tree.child(i).y;
        distance(i) = sqrt(dx^2 + dy^2);
        i = i+1;
    end
    [~,min_idx] = min(distance);
    angle = atan2(rd_y-tree.child(min_idx).y, rd_x-tree.child(min_idx).x);
end

RRT_learn.m

%%
clear all
clc
%% Notification
% 1,用户自定义的内容：地图范围，障碍物数量和大小，起点和终点的位置，终点范围的阈值，RRT树生长一次的长度，和绘图相关的设置
% 2,需要演示算法效果的时候，把所有pause取消注释；不需要演示算法效果的时候，把所有pause加上注释
%% Define the map
resolution = 1; % resolution, cell length

left_bound = -15;
right_bound = 15;
lower_bound = -15;
upper_bound = 15;

% Wall obstacle [left_down_x,left_down_y,horizontal_length,vertical_length]
wall_obstacle(1,:) = [   left_bound,   lower_bound,                        1, upper_bound-lower_bound-1]; % left boundary
wall_obstacle(2,:) = [ left_bound+1,   lower_bound, right_bound-left_bound-1,                         1]; % bottom boundary
wall_obstacle(3,:) = [right_bound-1, lower_bound+1,                        1, upper_bound-lower_bound-1]; % right boundary
wall_obstacle(4,:) = [   left_bound, upper_bound-1, right_bound-left_bound-1,                         1]; % up boundary

% Blcok obstacle [left_down_x,left_down_y,horizontal_length,vertical_length]
block_obstacle(1,:) = [0,-10,10,5]; % block obstacle 1
block_obstacle(2,:) = [-5,5,5,9]; % block obstacle 2
block_obstacle(3,:) = [-5,-2,5,4]; % block obstacle 3

ob = [block_obstacle; wall_obstacle];
%% Draw the map
figure(1); % create a figure

% Figure setting
set(gca,'XLim',[left_bound right_bound]); % x axis range
set(gca,'XTick',[left_bound:resolution:right_bound]); % x axis tick
set(gca,'YLim',[lower_bound upper_bound]); % y axis range
set(gca,'YTick',[lower_bound:resolution:upper_bound]); % y axis tick
grid on
axis equal
title('RRT');
xlabel('x');
ylabel('y');

hold on

% Draw the obstacles
for i=1:1:size(ob,1)
    fill([ob(i,1),ob(i,1)+ob(i,3),ob(i,1)+ob(i,3),ob(i,1)],...
         [ob(i,2),ob(i,2),ob(i,2)+ob(i,4),ob(i,2)+ob(i,4)],'k');
end

%% Initialize parameters
grow_distance = 1; % distance between parent node and the derived child node
goal_radius = 1.5; % can be considered as reaching the goal once within this range
% Goal point position
goal.x = -10;
goal.y = -10;
% Start point position
start.x = 13;
start.y = 10;
%% Draw the start point and the end point
h_start = plot(start.x,start.y,'b^','MarkerFaceColor','b','MarkerSize',5*resolution);
h_goal = plot(goal.x,goal.y,'m^','MarkerFaceColor','m','MarkerSize',5*resolution);

% Draw the goal circle
theta = linspace(0,2*pi);
goal_circle.x = goal_radius*cos(theta) + goal.x;
goal_circle.y = goal_radius*sin(theta) + goal.y;
plot(goal_circle.x,goal_circle.y,'--k','LineWidth',0.8*resolution);
%% RRT Algorithm
% Initialize the random tree(in the form of struct)
tree.child = []; % current node
tree.parent = []; % current node's parent
tree.distance = []; % current node's distance to the start

tree.child = start;
tree.parent = start;
tree.distance = 0;

new_node.x = start.x;
new_node.y = start.y;

goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);

% Main loop
while goal_distance > goal_radius
    random_point.x = (right_bound - left_bound) * rand() + left_bound; % random x value between x limit
    random_point.y = (upper_bound - lower_bound) * rand() + lower_bound; % random y value between y limit
    handle_1 = plot(random_point.x,random_point.y,'p','MarkerEdgeColor',[0.9290 0.6940 0.1250],'MarkerFaceColor',[0.9290 0.6940 0.1250],'MarkerSize',8*resolution); % draw the randomly generated point
    [angle,min_idx] = find_closest_node(random_point.x,random_point.y,tree);
    
    % pause(0.5)
    handle_2 = plot([tree.child(min_idx).x,random_point.x],[tree.child(min_idx).y,random_point.y],'-','Color',[0.7 0.7 0.7],'LineWidth',0.8*resolution); % draw the segment between the closest tree node and the randomly generated point
    
    % pause(0.5)
    new_node.x = tree.child(min_idx).x + grow_distance*cos(angle);
    new_node.y = tree.child(min_idx).y + grow_distance*sin(angle);
    handle_3 = plot(new_node.x,new_node.y,'.r','MarkerFaceColor','r','MarkerSize',10*resolution); % draw the potential new node
    
    flag = 1; % default: valid node

    % Judge if the new node is inside the obstacle
    step = 0.01;
    if new_node.x < tree.child(min_idx).x
        step = -step;
    end
    for k=1:1:size(ob,1)
        for i=tree.child(min_idx).x:step:new_node.x
            if angle>pi/2-5e-02 && angle<pi/2+5e-02
                j = tree.child(min_idx).y+1;
            elseif angle>-pi/2-5e-02 && angle<-pi/2+5e-02
                j = tree.child(min_idx).y-1;
            else
                j=tree.child(min_idx).y+(i-tree.child(min_idx).x)*tan(angle);
            end
            if i>=ob(k,1) && i<=(ob(k,1)+ob(k,3))
                if j >=ob(k,2) && j<=ob(k,2)+ob(k,4)
                    flag = 0; % invalid node
                    break
                end
            end
        end
        if flag==0
            break
        end
    end

    % pause(0.5)
    if flag==1
        tree.child(end+1) = new_node;
        tree.parent(end+1) = tree.child(min_idx);
        tree.distance(end+1) = 1 + tree.distance(min_idx);
        goal_distance = sqrt((goal.x - new_node.x)^2 + (goal.y - new_node.y)^2);
        delete(handle_3)
        plot(new_node.x,new_node.y,'.g','MarkerFaceColor','g','MarkerSize',10*resolution); % draw the new node
        % pause(0.2)
        plot([tree.child(min_idx).x,new_node.x],[tree.child(min_idx).y,new_node.y],'-k','LineWidth',0.8*resolution); % draw the segment between the closest tree node and the new node
    end
    
    % pause(0.5)
    delete(handle_1);
    delete(handle_2);
    % pause(0.5)
end

%% Draw the final path
final_distance = tree.distance(end);
title('RRT, distance:',num2str(final_distance));

current_index = length(tree.child);
while current_index ~= 1
    plot([tree.child(current_index).x,tree.parent(current_index).x],[tree.child(current_index).y,tree.parent(current_index).y],'-','LineWidth',1.5*resolution,'Color',[0.8500 0.3250 0.0980]); % draw the segment between the closest tree node and the new node    
    for i=1:length(tree.child)
        if tree.child(i).x == tree.parent(current_index).x
            if tree.child(i).y == tree.parent(current_index).y
                current_index = i;
                break
            end
        end
    end
end