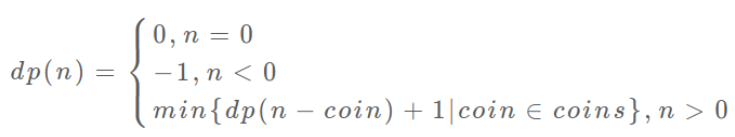Codeforces Round 918 (Div. 4)
G. Bicycles
G. Bicycles
题意:
斯拉夫的所有朋友都打算骑自行车从他们住的地方去参加一个聚会。除了斯拉维奇,他们都有一辆自行车。他们可以经过 n n n 个城市。他们都住在城市 1 1 1 ,想去参加位于城市 n n n 的聚会。城市地图可以看作一个无向图,有 n n n 个节点和 m m m 条边。边 i i i 连接城市 u i u_i ui 和 v i v_i vi ,长度为 w i w_i wi 。
斯拉夫没有自行车,但他有的是钱。每个城市都有一辆自行车出售。在 i i i 这个城市中,自行车的速度系数为 s i s_{i} si 。一旦斯拉维奇买了一辆自行车,他就可以在任何时候用它从他现在所在的城市前往任何邻近的城市,只需花费 w i ⋅ s j w_i \cdot s_j wi⋅sj 时间,因为他是在用自己拥有的自行车 j j j 穿越边缘 i i i 。
斯拉维奇想买多少辆自行车都可以,因为钱对他来说不是问题。由于斯拉维奇不喜欢骑自行车旅行,他希望在最短的时间内从他的住处到达聚会地点。由于他的信息技能很生疏,他需要你的帮助。
斯拉夫从城市 1 1 1 到城市 n n n 所需的最短时间是多少?斯拉夫没有自行车就无法旅行。保证斯拉夫可以从城市 1 1 1 到达其他任何城市。
思路:
很好的一个变型dijkstra。先放一下dijkstra的证明过程:


写的很抽象,但是证明思路很明显:如果我们从堆里所有状态中选出走过的路长度最少的状态,如果这个状态所在位置之前还没有被访问过,那么现在这个状态走过的路长度就是最短的,我的意思是,之后到达这个位置的最短路径就再也不可能被刷新了。证明是显然的:现在所有状态走过的路的长度都大于这个状态,我们继续走下去只会使得走的路变长,无论从什么状态来推,之后到达的时候长度一定不可能小于现在的长度了。
一眼看下来感觉应该是个最短路问题,用dijkstra,但是由于我们可以先去一个其他城市买到一个更快的车子,然后用这个车子到达终点,结果可能更优,所以直接跑dij是不对的。
考虑到我们到一个城市的时候只看原点到它的距离,而不看手上的自行车是有可能不优的。但是如果多存储一维自行车的慢速因子来描述我们到这个城市的距离就是最优的了。具体来说,原本的 d i s dis dis 数组设为 d i s [ u ] [ b i k e ] dis[u][bike] dis[u][bike] ,表示到达城市 u u u,手上最快的自行车为 b i k e bike bike 的最短距离,这样 u , b i k e u,bike u,bike 确定时,距离一定是越小越好的,而不会对后面产生影响。
做法就出来了。 d i s dis dis 数组多描述一维自行车的慢速因子,优先队列存储的状态多存储一个手上最快的自行车的信息就可以了。这里因为我们自行车一定是会越来越快的,而我们经过的点最长是,先到一个城市买最快的自行车,再回来走到终点,因此时间复杂度差不多是 O ( 2 n m l o g n ) O(2nmlogn) O(2nmlogn) 的。
到达某个点,带有某个自行车的最近距离,这里其实很像动态规划的思想。不如说,dijkstra本身就很有动态规划的味道。比较类似的有这里的E题
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int maxn=1005;
const ll inf=1e9;
int T,n,m;
int head[maxn],counter;
struct EDGE{
int v,w,nxt;
}e[maxn<<1];
void adde(int u,int v,int w){
e[++counter].v=v;
e[counter].w=w;
e[counter].nxt=head[u];
head[u]=counter;
}
void init(){
cin>>n>>m;
memset(head,0,sizeof(head));
counter=0;
for(int i=1,u,v,w;i<=m;i++){
cin>>u>>v>>w;
adde(u,v,w);
adde(v,u,w);
}
}
struct node{
ll cost;
int bike,u;
bool operator<(const node &x)const{
return (cost==x.cost)?bike>x.bike:cost>x.cost;
}
};
int s[maxn];
ll d[maxn][maxn];
ll dijkstra(){
memset(d,0x3f,sizeof(d));
priority_queue<node> h;
d[1][s[1]]=0;
h.push(node{1,s[1],1});
while(!h.empty()){
int u=h.top().u,bike=h.top().bike;
h.pop();
if(u==n)return d[u][bike];
if(bike>s[u]){
d[u][s[u]]=min(d[u][s[u]],d[u][bike]);
bike=s[u];
}
for(int i=head[u],v,w;i;i=e[i].nxt){
v=e[i].v;w=e[i].w;
if(d[v][bike]>d[u][bike]+1ll*bike*w){
d[v][bike]=d[u][bike]+1ll*bike*w;
h.push(node{d[v][bike],bike,v});
}
}
}
return inf;
}
int main(){
cin>>T;
while(T--){
init();
for(int i=1;i<=n;i++)
cin>>s[i];
cout<<dijkstra()<<endl;
}
return 0;
}





![[极客大挑战 2019]LoveSQL1 题目分析与详解](https://img-blog.csdnimg.cn/direct/0d2b7db092a1482e9042137ee336ffad.png)