论文:A new approach to linear filtering and prediction problems http://160.78.24.2/Public/Kalman/Kalman1960.pdf
状态空间模型介绍
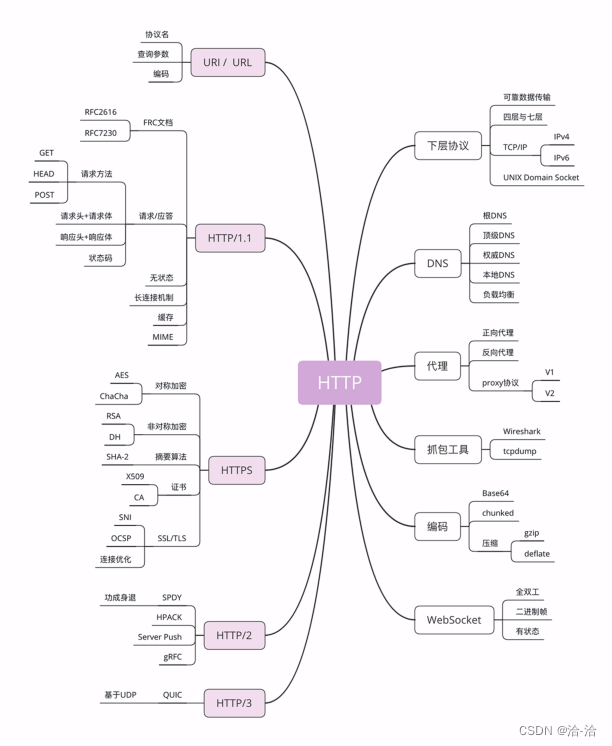
术语状态空间模型具有非常广泛的含义,它简单地表示任何具有潜在状态的循环过程的概念。 它已被用来指代不同学科中的许多不同概念,包括马尔可夫决策过程 (MDP)(强化学习(Hafner 等人,2020))、动态因果建模(DCM)(计算神经科学(Friston、Harrison 和 Penny 2003) ))、卡尔曼滤波器(控制(Kalman 1960))、隐马尔可夫模型(HMM)和线性动力系统(LDS)(机器学习)以及循环(有时是卷积)模型(深度学习)。
状态空间模型是一种描述动态系统行为的数学模型,它使用一组一阶微分方程(连续时间系统)或差分方程(离散时间系统)来表示系统的内部状态的演化,同时用另一组方程来描述系统状态和输出之间的关系。这些方程可以表示为矩阵和向量的形式,以处理多变量系统。
在状态空间表述中,系统由下面的两个方程组定义。SSM将一个1-D的输入向量
u
(
t
)
u(t)
u(t)映射为一个N-D的潜在状态变量
x
(
t
)
x(t)
x(t),然后再映射为一个1-D的输出向量
y
(
t
)
y(t)
y(t)。我们的目标是将这个SSM作为黑盒转化为深度模型,其中参数F、D、M、G通过梯度下降等方法学习,并且参数G可以省略,因为参数G的作用类似残差网络的跳跃链接。
- 状态方程:
x ′ ( t ) = F x ( t ) + D u ( t ) + ω ( t ) x'(t) = Fx(t) + Du(t) + \omega(t) x′(t)=Fx(t)+Du(t)+ω(t)** 公式(1) **
这个方程描述了系统内部状态 x ( t ) x(t) x(t)随时间的演化。这里:
- x ( t ) x(t) x(t) 是系统状态变量,包含所有必要的变量来描述系统在任意时刻的状况,是一个 n n n维向量。
- x ′ ( t ) x'(t) x′(t) 是 x ( t ) x(t) x(t) 关于时间的微分,表示系统状态的变化率。
- F F F 是系统矩阵,描述了系统状态之间的关系,以及它们如何随时间自然演化(无控制输入时),是一个 n × n n \times n n×n矩阵。
- u ( t ) u(t) u(t) 是控制输入向量,表示外部输入或控制信号的影响,是一个 m m m维向量,并且 m ≤ n m \le n m≤n。
- D D D 是输入矩阵,描述了控制输入如何影响系统状态,是一个 n × m n \times m n×m矩阵。
- ω ( t ) \omega(t) ω(t)是过程噪声,它代表系统内部的不确定性,一般假设为高斯噪声。
- 观测方程:
y ( t ) = M x ( t ) + G u ( t ) + e ( t ) y(t) = Mx(t) + Gu(t) + e(t) y(t)=Mx(t)+Gu(t)+e(t)** 公式(2)**
这个方程描述了系统的输出 y ( t ) y(t) y(t) 如何依赖于系统状态和控制输入。这里:
- y ( t ) y(t) y(t)是输出向量或者观测向量,包含所有的测量或观测到的变量,是一个 p p p维向量,并且 p ≤ n p \le n p≤n矩阵。
- M M M是输出矩阵,描述了系统状态如何影响输出,是一个 p ≤ n p \le n p≤n矩阵。
- G G G是直达传递矩阵(在很多实际系统中,这个矩阵通常是零或者不显著),表示控制输入直接对输出的影响,是一个 n × m n \times m n×m矩阵。
- e ( t ) e(t) e(t)是测量噪声,它代表了测量过程中的不确定性或误差,一般假设为高斯噪声。
用下图可以说明这个过程。
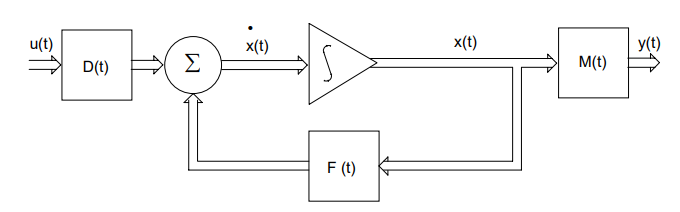
状态空间模型离散化
将状态空间模型从连续过程转换为离散过程是控制理论和信号处理中的一个常见任务,因为数字计算机和微控制器通常只能处理离散时间信号。为了在数字设备上实现卡尔曼滤波器,我们需要将连续时间下的状态空间模型离散化。
连续时间状态空间模型通常表示为微分方程的形式:
x
˙
(
t
)
=
A
(
t
)
x
(
t
)
+
B
(
t
)
u
(
t
)
\dot{\mathbf{x}}(t) = \mathbf{A}(t) \mathbf{x}(t) + \mathbf{B}(t) \mathbf{u}(t)
x˙(t)=A(t)x(t)+B(t)u(t)
y
(
t
)
=
C
(
t
)
x
(
t
)
+
D
(
t
)
u
(
t
)
\mathbf{y}(t) = \mathbf{C}(t) \mathbf{x}(t) + \mathbf{D}(t) \mathbf{u}(t)
y(t)=C(t)x(t)+D(t)u(t)
这里,
x
(
t
)
\mathbf{x}(t)
x(t) 是状态向量,
u
(
t
)
\mathbf{u}(t)
u(t) 是输入向量,
y
(
t
)
\mathbf{y}(t)
y(t)是输出向量,
A
(
t
)
\mathbf{A}(t)
A(t),
B
(
t
)
\mathbf{B}(t)
B(t),
C
(
t
)
\mathbf{C}(t)
C(t), 和
D
(
t
)
\mathbf{D}(t)
D(t) 分别是系统矩阵。
离散化过程涉及以下步骤:
- 采样时间的选择:
- 确定一个合适的采样时间间隔 Δ t \Delta t Δt,这个时间间隔要基于系统动态特性以及所需的控制精度。
- 离散化系统矩阵:
- 使用适当的数值方法将连续系统矩阵
A
(
t
)
\mathbf{A}(t)
A(t)和
B
(
t
)
\mathbf{B}(t)
B(t) 转换为离散矩阵
A
d
\mathbf{A}_d
Ad_ 和 _
B
d
\mathbf{B}_d
Bd。最常见的方法是指数映射(也称为矩阵指数):
A d = e A Δ t \mathbf{A}_d = e^{\mathbf{A}\Delta t} Ad=eAΔt
B d = ( ∫ 0 Δ t e A τ d τ ) B \mathbf{B}_d = (\int{0}^{\Delta t} e^{\mathbf{A}\tau} d\tau) \mathbf{B} Bd=(∫0ΔteAτdτ)B - 这些公式适用于时间不变系统。对于时间变化系统,需要更复杂的积分或数值分析方法。
- 离散化状态和输出方程:
- 确定的离散时间点
t
k
=
k
Δ
t
t_k = k\Delta t
tk=kΔt 上的状态和输出方程可以表示为:
x [ k + 1 ] = A d x [ k ] + B d u [ k ] \mathbf{x}[k+1] = \mathbf{A}_d \mathbf{x}[k] + \mathbf{B}_d \mathbf{u}[k] x[k+1]=Adx[k]+Bdu[k]
y [ k ] = C d x [ k ] + D d u [ k ] \mathbf{y}[k] = \mathbf{C}_d \mathbf{x}[k] + \mathbf{D}_d \mathbf{u}[k] y[k]=Cdx[k]+Ddu[k] - 其中, C d \mathbf{C}_d Cd_和 _ D d \mathbf{D}_d Dd 通常可以直接等同于连续时间模型中的 C \mathbf{C} C 和 D \mathbf{D} D,除非输出方程也涉及时间的导数。
一旦连续系统被转换为离散系统,就可以使用离散时间的卡尔曼滤波器来估计系统的状态。注意,离散化过程必须保留系统的关键动态特性,而且采样时间必须遵守奈奎斯特采样定理,以避免混叠现象。
用下图可以说明这个过程。
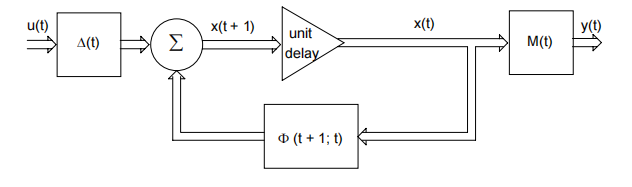
卡尔曼滤波器
我们可以使用卡尔曼滤波器解决状态空间方程。
卡尔曼滤波器用于解决状态空间模型中的估计问题时,分为两个阶段:预测阶段和更新阶段。状态空间模型通常由两个方程定义:状态方程和观测方程。
状态方程描述了系统状态的时间演化,通常形式为:
x
k
=
F
k
x
k
−
1
+
B
k
u
k
+
w
k
\mathbf{x}_k = \mathbf{F}_k \mathbf{x}_{k-1} + \mathbf{B}_k \mathbf{u}_k + \mathbf{w}_k
xk=Fkxk−1+Bkuk+wk
其中,
- x k \mathbf{x}_k xk 是时间点 (k) 的状态向量。
- F k \mathbf{F}_k Fk是状态转移矩阵,描述了状态如何从时间 k − 1 k-1 k−1到 k k k 转移。
- B k \mathbf{B}_k Bk_是控制输入矩阵,将控制向量 _ u k \mathbf{u}_k uk 的影响加入状态转移。
- w k \mathbf{w}_k wk 是系统过程噪声,通常假设为高斯白噪声。
观测方程描述了如何从状态向量得到观测量,形式为:
z
k
=
H
k
x
k
+
v
k
\mathbf{z}_k = \mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k
zk=Hkxk+vk
其中,
- z k \mathbf{z}_k zk 是时间点 (k) 的观测向量。
- H k \mathbf{H}_k Hk 是观测矩阵,将状态空间映射到观测空间。
- v k \mathbf{v}_k vk是观测噪声,通常也假设为高斯白噪声。
现在我们来看卡尔曼滤波器如何工作:
- 初始化:
- 估计初始状态 x ^ 0 \hat{\mathbf{x}}_0 x^0_和初始误差协方差矩阵 _ P 0 \mathbf{P}_0 P0。
- 预测阶段(Predict):
- 用状态方程预测下一个状态
x
^
k
−
\hat{\mathbf{x}}_k^-
x^k−:
x ^ k − = F k − 1 x ^ k − 1 + B k − 1 u k − 1 \hat{\mathbf{x}}_k^- = \mathbf{F}_{k-1} \hat{\mathbf{x}}_{k-1} + \mathbf{B}_{k-1} \mathbf{u}_{k-1} x^k−=Fk−1x^k−1+Bk−1uk−1 - 估计预测状态的误差协方差
P
k
−
\mathbf{P}_k^-
Pk−:
P k − = F k − 1 P k − 1 F k − 1 T + Q k − 1 \mathbf{P}_k^- = \mathbf{F}_{k-1} \mathbf{P}_{k-1} \mathbf{F}_{k-1}^T + \mathbf{Q}_{k-1} Pk−=Fk−1Pk−1Fk−1T+Qk−1 - 其中, Q k − 1 \mathbf{Q}_{k-1} Qk−1 是过程噪声协方差矩阵,表示模型的不确定性。
- 更新阶段(Update):
- 计算卡尔曼增益
K
k
\mathbf{K}_k
Kk:
K k = P k − H k T ( H k P k − H k T + R k ) − 1 \mathbf{K}_k = \mathbf{P}_k^- \mathbf{H}_k^T (\mathbf{H}_k \mathbf{P}_k^- \mathbf{H}_k^T + \mathbf{R}_k)^{-1} Kk=Pk−HkT(HkPk−HkT+Rk)−1 - 其中, R k \mathbf{R}_k Rk是观测噪声协方差矩阵。
- 用观测值更新预测的状态:
x ^ k = x ^ k − + K k ( z k − H k x ^ k − ) \hat{\mathbf{x}}_k = \hat{\mathbf{x}}_k^- + \mathbf{K}_k (\mathbf{z}_k - \mathbf{H}_k \hat{\mathbf{x}}_k^-) x^k=x^k−+Kk(zk−Hkx^k−) - 更新误差协方差矩阵:
P k = ( I − K k H k ) P k − \mathbf{P}_k = (I - \mathbf{K}_k \mathbf{H}_k) \mathbf{P}_k^- Pk=(I−KkHk)Pk−这个过程会不断迭代,随着新的观测数据的到来,卡尔曼滤波器会继续预测和更新系统的状态。卡尔曼滤波器的优势在于它能够在存在噪声的情况下,提供实时的最优估计。此外,卡尔曼滤波器是最小均方误差(MMSE)估计的一种实现,能够确保估计误差的协方差最小化。