1.前言
本题需要结构体和数组的知识,记录每天的刷题,继续坚持!
2.OJ题目训练
设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。Front: 从队首获取元素。如果队列为空,返回 -1 。Rear: 获取队尾元素。如果队列为空,返回 -1 。enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。isEmpty(): 检查循环队列是否为空。isFull(): 检查循环队列是否已满。示例:
MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3 circularQueue.enQueue(1); // 返回 true circularQueue.enQueue(2); // 返回 true circularQueue.enQueue(3); // 返回 true circularQueue.enQueue(4); // 返回 false,队列已满 circularQueue.Rear(); // 返回 3 circularQueue.isFull(); // 返回 true circularQueue.deQueue(); // 返回 true circularQueue.enQueue(4); // 返回 true circularQueue.Rear(); // 返回 4提示:
- 所有的值都在 0 至 1000 的范围内;
- 操作数将在 1 至 1000 的范围内;
- 请不要使用内置的队列库。
题目分析
本体是为了实现循环使用的“队列”数据结构,但是我们用队列会很难实现,因为涉及到,会删除数据并且重复使用空间,所以我们运用数组来实现最为方便
题解
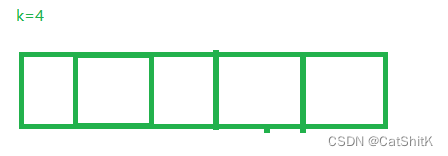
假设题目需要的k(空间大小)为4,那么我们可以设计5个空间的数组,以便指针方便使用
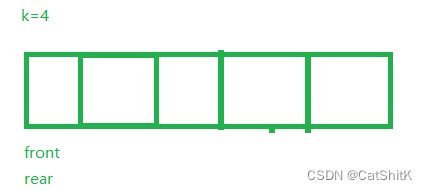
数组头指针定义两个指针分别为头、尾指针,当他们相等时,数组为空
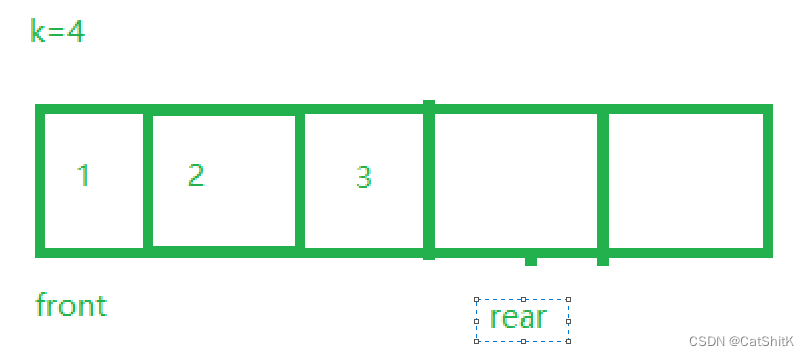
添加数据时,rear移动,添加数据
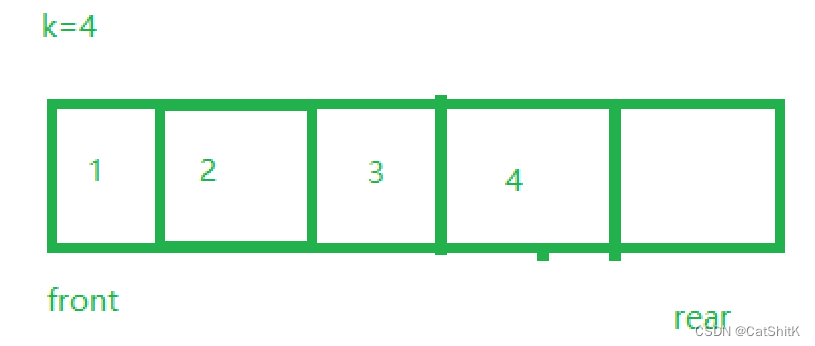
当添加四个数据后,空间需求已满,我们前面是rear自加1来移动rear的位置,当此处rear和front相差1的距离来代表数组已满,我们就可以让rear+1,在%5,如果等于front,就代表此数组已满
rear+1 = 6, 6%5 = 1, front = 1 ;
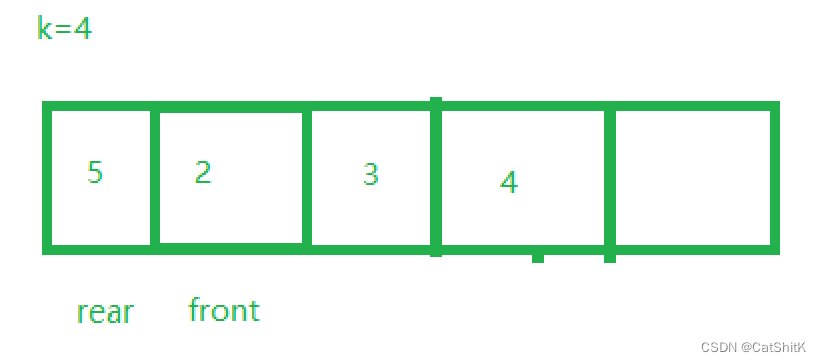
此公式同时适用于其他任何情况,例如现在front被抹去了一个数据,先前移动了一位,rear也添加了一个5的数据,这样用(rear+1)%(k+1) == obj->front; (k=4 )也能判断
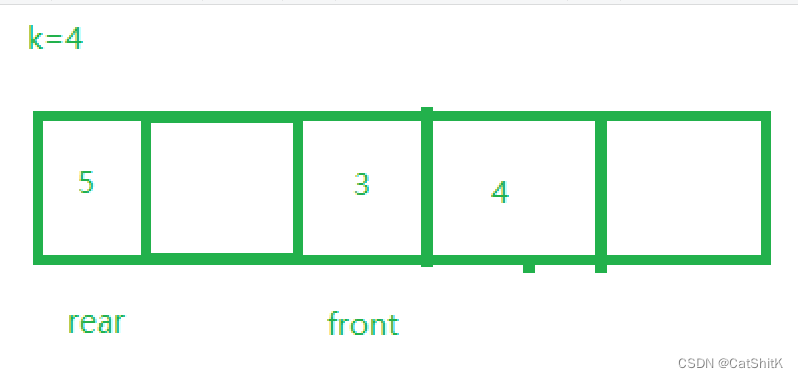
同理如果移除数据,那就改变front向前移动,直到front和rear相等,数组为空,才不能继续删除
注意事项
- 每次使用rear和front指针走到超过(k+1)时,就代表已经越界,那么就需要通过取模来进行复位到1
- 当front和rear相等为空,rear+1%(k+1) == front为满.
附源代码
typedef struct {
int * a;
int front;
int rear;
int k;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc(sizeof(int)*(k+1));
obj->front = obj->rear = 0;
obj->k = k;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->rear == obj->front;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear+1)%(obj->k+1) == obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
return false;
obj->a[obj->rear]=value;
obj->rear++;
obj->rear%=(obj->k+1);
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return false;
++obj->front;
obj->front %= (obj->k+1);
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->a[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->a[(obj->rear+obj->k)% (obj->k+1)];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
/**
* Your MyCircularQueue struct will be instantiated and called as such:
* MyCircularQueue* obj = myCircularQueueCreate(k);
* bool param_1 = myCircularQueueEnQueue(obj, value);
* bool param_2 = myCircularQueueDeQueue(obj);
* int param_3 = myCircularQueueFront(obj);
* int param_4 = myCircularQueueRear(obj);
* bool param_5 = myCircularQueueIsEmpty(obj);
* bool param_6 = myCircularQueueIsFull(obj);
* myCircularQueueFree(obj);
*/