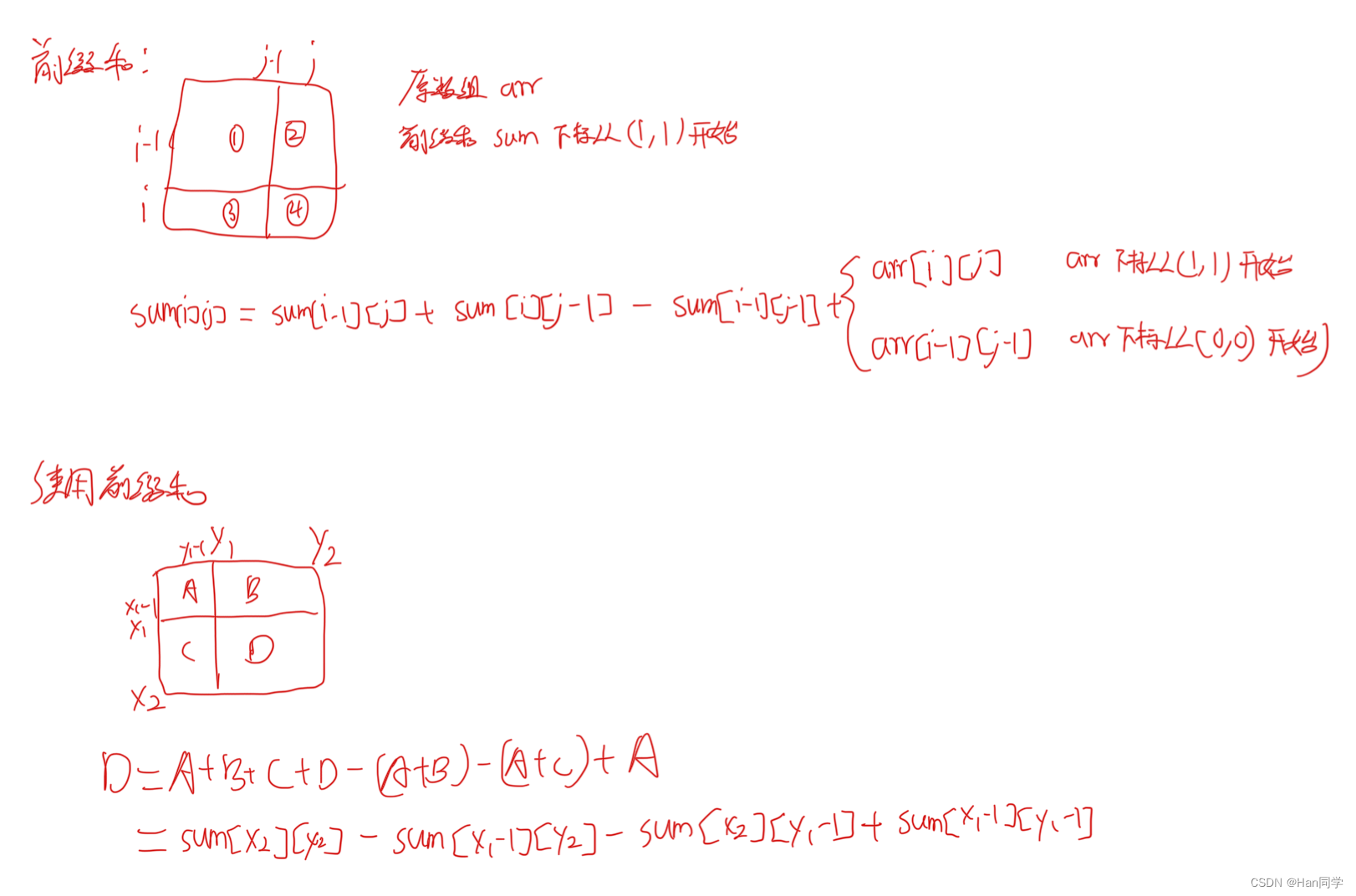目录
1、DP34 【模板】前缀和
2、DP35 【模板】二维前缀和编辑
3、724. 寻找数组的中心下标
4、238. 除自身以外数组的乘积
5、560. 和为 K 的子数组
6、974. 和可被 K 整除的子数组
7、525. 连续数组
8、1314. 矩阵区域和
1、DP34 【模板】前缀和

思路:注意题中数组下标从1开始!!!
- 我们使用一个循环遍历数组
arr中的每个元素,并计算前缀和。在每次迭代中,我们将当前元素arr[i]加到前一个前缀和a[i-1]上,得到新的前缀和a[i]。这样,我们就可以通过累加数组元素来计算前缀和。- 具体地,
a[i] = a[i - 1] + arr[i]表示第i个元素的前缀和等于前一个前缀和加上当前元素的值。这样,我们就可以通过一次遍历计算出整个数组的前缀和。
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, q;
cin >> n >> q;
vector<int> arr(n + 1);
for (int i = 1; i < n + 1; i++) {
cin >> arr[i];
}
vector<long long> a(n + 1);
for (int i = 1; i < n + 1; i++) {
a[i] = a[i - 1] + arr[i];
}
int l = 0, r = 0;
while (q--) {
cin >> l >> r;
cout << a[r] - a[l - 1] << endl;
}
return 0;
}2、DP35 【模板】二维前缀和
思路:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n = 0, m = 0, q = 0;
cin >> n >> m >> q;
vector<vector<int>> arr(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> arr[i][j];
}
}
vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
}
}
int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
while (q--) {
cin >> x1 >> y1 >> x2 >> y2;
cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]<<endl;
}
}3、724. 寻找数组的中心下标

思路:
- 前缀和数组:a[i]表示[0,i-1]区间所有元素的和:a[i]=a[i-1]+nums[i-1]
- 后缀和数组:b[i]表示[i+1,n-1]区间所有元素的和:b[i]=b[i+1]+nums[i+1]
- 处理边界:f(0)=0,g(n-1)=0
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
vector<int> lsum(n), rsum(n);
for (int i = 1; i < n; i++) {
lsum[i] = lsum[i - 1] + nums[i - 1];
}
for (int j = n - 2; j >= 0; j--) {
rsum[j] = rsum[j + 1] + nums[j + 1];
}
for (int i = 0; i < n; i++) {
if (lsum[i] == rsum[i])
return i;
}
return -1;
}
};4、238. 除自身以外数组的乘积

思路:
- f:表示前缀积:f[i]表示:[0,i-1]区间内所有元素的乘积:f[i]=f[i-1]*nums[i-1]
- g:表示后缀积:g[i]表示:[i+1,n-1]区间内所有元素的乘积:g[i]=g[i+1]*nums[i+1]
- 处理边界:f(0)=1,g(n-1)=1
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> lsum(n), rsum(n);
lsum[0] = rsum[n - 1] = 1;
for (int i = 1; i < n; i++) {
lsum[i] = lsum[i - 1] * nums[i - 1];
}
for (int i = n - 2; i >= 0; i--) {
rsum[i] = rsum[i + 1] * nums[i + 1];
}
vector<int> ret(n);
for (int i = 0; i < n; i++) {
ret[i] = lsum[i] * rsum[i];
}
return ret;
}
};5、560. 和为 K 的子数组

思路:前缀和+哈希表(记录前缀和出现次数)统计sum-k出现次数。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> hash;
hash[0] = 1;
int sum = 0, ret = 0;
for (auto a : nums) {
sum += a;
//如sum-k存在,则证明当前和为k或存在两段连续区间相减后和为k
if (hash.count(sum - k))
ret += hash[sum - k];
hash[sum]++;
}
return ret;
}
};6、974. 和可被 K 整除的子数组

思路:前缀和+哈希表(记录前缀和出现次数),其中,需要使用(sum % k + k) % k,对sum可能为负数的情况进行修正。
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int, int> hash;
hash[0] = 1;
int sum = 0, ret = 0;
for (auto a : nums) {
sum += a;
int r = (sum % k + k) % k;
if (hash.count(r))
ret += hash[r];
hash[r]++;
}
return ret;
}
};7、525. 连续数组

思路:前缀和+哈希表(记录前缀和出现位置),将0当作-1,转化为计算和为0的区间长度。
- 将所有的0修改成-1;
- 在数组中,找出最长的子数组使子数组中所有元素的和为0
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int, int> hash;
hash[0] = -1;
int sum = 0, ret = 0;
for (int i = 0; i < nums.size(); i++) {
sum += nums[i] == 0 ? -1 : 1;
if (hash.count(sum))
ret = max(ret, i - hash[sum]);
else
hash[sum] = i;
}
return ret;
}
};8、1314. 矩阵区域和

思路: 二维前缀和
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + mat[i - 1][j - 1] -
dp[i - 1][j - 1];
}
}
vector<vector<int>> ret(m, vector<int>(n));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +
dp[x1 - 1][y1 - 1];
}
}
return ret;
}
};int m = mat.size(), n = mat[0].size();: 这里获取矩阵的行数 m 和列数 n。
vector<vector<int>> dp(m + 1, vector<int>(n + 1));: 创建一个大小为 (m+1) x (n+1) 的二维数组 dp,用于存储矩阵的前缀和。
使用一个嵌套循环,用于计算矩阵的前缀和。通过动态规划的思想,dp[i][j] 表示以 (i-1, j-1) 为右下角的子矩阵的元素和。通过递推公式 dp[i][j] = dp[i-1][j] + dp[i][j-1] + mat[i-1][j-1] - dp[i-1][j-1],可以计算出每个位置的前缀和。
vector<vector<int>> ret(m, vector<int>(n));: 创建一个大小为 m x n 的二维数组 ret,用于存储最终的结果。
第二个嵌套循环,用于计算每个位置 (i, j) 的区域和。通过利用前缀和数组 dp,根据题目给出的条件计算出满足条件的元素和。
x1 = max(0, i - k) + 1和y1 = max(0, j - k) + 1确定了左上角的坐标。x2 = min(m - 1, i + k) + 1和y2 = min(n - 1, j + k) + 1确定了右下角的坐标。ret[i][j]计算了以(i, j)为中心,边长为2k+1的正方形区域内的元素和。
最后,函数返回结果矩阵 ret,其中每个元素 ret[i][j] 是满足条件的元素和。