矩阵的范数 matrix norm Frobenius norm 弗罗贝尼乌斯范数

news2025/2/25 5:35:10

1，矩阵范数的定义

矩阵的范数，matrix norm即矩阵的模；它把一个矩阵空间变成为赋范线性空间；

从一个矩阵空间映射到非负实数的函数 $\parallel.\parallel$ 满足以下条件：

1，严格的正定性。对于 $\forall A \in \mathbf{M}_{m,n}(\mathbb{K})$ , 则 $\parallel \mathbf{A} \parallel \ge \mathbf{0}$ ;

and if $\parallel \mathbf{A} \parallel = \mathbf{0}$ , must $\mathbf{A} = \mathbf{0}$ ;

2，线性性。 $\forall \alpha \in \mathbb{K}, \forall \mathbf{A}\in \mathbf{M}_{m,n}(\mathbb{K}),$ 都有 $\parallel \alpha \mathbf{A} \parallel = |\alpha| \parallel \mathbf{A} \parallel$

3，三角不等式。 $\forall \mathbf{A,B} \in \mathbf{M}_{m,n}(\mathbb{K})$ 都有 $\parallel \mathbf{A+B} \parallel \le \parallel \mathbf{A} \parallel + \parallel \mathbf{B} \parallel$

则 $\parallel . \parallel$ 是矩阵的一个范数 norm。

满足以上定义的范数有很多，大体分为元范数和诱导范数。

2，元范数

这类似一维的向量范数，

$\parallel \mathbf{A} \parallel = \left( \sum_{i=1}^{m}\sum_{j=1}^n |a_{ij}|^p \right )^{1/p}$

3，诱导范数

也称为诱导p-范数

$\parallel \mathbf{A} \parallel = max_{{i\ne 0}}\left( \frac{\parallel Ax\parallel_p}{\parallel x\parallel_p}\right) = max_{x\ne 0}\left( \frac {\left(\sum_{i=1}^m|\sum_{j=1}^na_{ij}x_j|^p \right )^{1/p}} {\left(\sum_{j=1}^{n}{|x_j|}^{p} \right )^{1/p}} \right)$

p = 1

$\parallel \mathbf{A}\parallel _1 = max_{1\le j \le n}\sum_{i=1}^m|a_{ij}|$ 即，列元素绝对值之和的最大者

p = $\infty$

$\parallel \mathbf{A} \parallel = max_{1\le i \le m}\sum_{j=1}^n|a_{ij}|$ 即，行元素绝对值之和的最大者

4，Frobenius 范数

p=2时，称为 Frobenius norm，或者希尔伯特-施密特范数， Hilbert-Schmidt norm，常用于希尔伯特空间：

$\parallel \mathbf{A} \parallel _F =\sqrt{\sum_{i=1}^m\sum_{j=1}^n|a_{ij}|^2} = \sqrt{trace\left({\mathbf{A^*}}\mathbf{A} \right )}=\sqrt{\sum_{i=1}^{min\{m,n\}}\sigma_i^2}$

其中， $A^*$ 是 A的共轭转置； $\sigma_j$ 是A的奇异值，trace()是迹函数。

5，总结

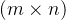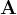综上所述，Frobenius norm 是元范数（element-wise norm），而不是诱导范数（induced norm）。它是矩阵元素的平方和的平方根，通常用于衡量矩阵的大小。对于一个 $( m \times n)$ 矩阵 $\mathbf{A}$ ，其Frobenius范数定义为：

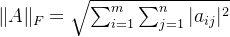
$\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} |a_{ij}|^2}$

这与诱导范数不同，而诱导范数是基于矩阵作为线性变换时的最大“拉伸”或“压缩”量，例如最常见的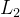 $L_2$ 诱导范数（或称谱范数）是基于矩阵的最大奇异值。